八皇后问题4种c语言算法

八皇后问题

1.递归回溯法

B站懒猫老师讲的（我在这里学的）
八皇后问题的递归回溯算法思路：从第一行开始当某一行皇后位置不与前面所有皇后位置冲突那么记录该行皇后位置并调用递归函数进入下一行，摆放下一个皇后，逐个位置摆放，若该行所有位置都被其他皇后占领，那么就回溯到上一行重新摆放上一行皇后直至所有皇后都不冲突那么记录一次方法然后回溯寻找其他摆放方法。

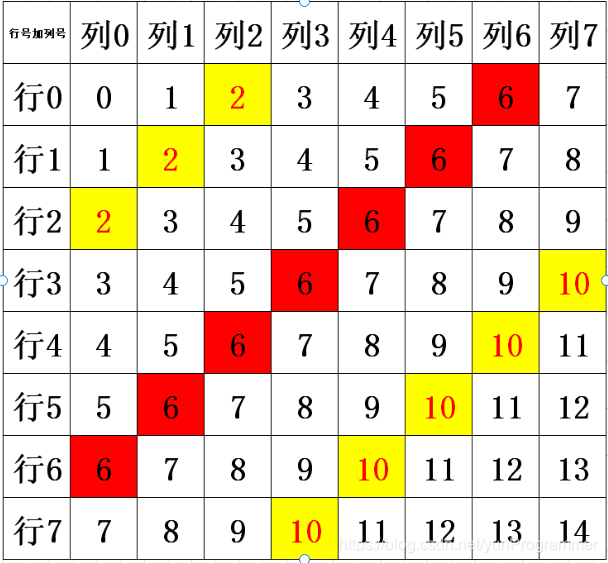
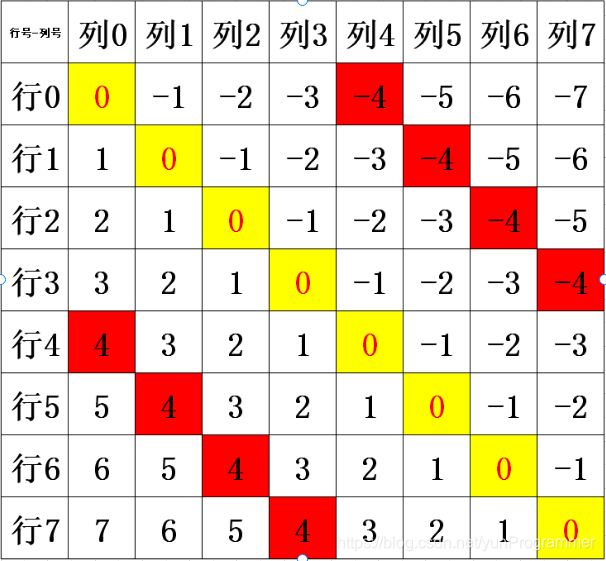
冲突算法思路：一个8*8的棋盘每一个位置若用其行号加上其列号我们可以得到下图，由图可知在同一条上对角线的数值都相同，因此我们可以利用该规律设计判断上对角线是否冲突的函数，类似的，下对角线则是由列号减去行号可得在同一条下对角线的数值相等。为了方便后面的程序中我把下对角线的数值都加7为正数（实际效果不变）
行号+列号
行号-列号

#include<stdio.h>
int place[8]={0};//皇后位置
bool flag[8]={1,1,1,1,1,1,1,1};//定义列
bool d1[15]={1,1,1,1,1,1,1,1,1,1,1,1,1,1,1};/*定义上对角线（共有15个对角线,
因此定义一个长度为15的bool型数组，初值为1代表该对角线没有被皇后占领，
若被皇后占领则赋值为0*/
bool d2[15]={1,1,1,1,1,1,1,1,1,1,1,1,1,1,1} ;//定义下对角线
int number=0;//记录输出次数
void print()//定义输出函数
{int col,i,j;
number++;//每调用一次输出函数number自加一次，记录摆放方法个数printf("No.%2d\n",number);int table[8][8]={0};//设置一个8*8的棋盘for (i=0;i<8;i++){table[i][place[i]]=1;//将每一行皇后所在位置赋值为1}for (i=0;i<8;i++){for (j=0;j<8;j++){printf("%d|",table[i][j]);}printf("\n");}
}
int queen(int n )//定义递归回溯函数
{int col;for (col=0;col<8;col++){if (flag[col]&&d1[n-col+7]&&d2[n+col])//判断皇后是否冲突{place[n]=col;//放置皇后flag[col]=false;d1[n-col+7]=false;d2[n+col]=false;//将该皇后所在的行、列、对角线设置为被占领if(n<7)	{queen(n+1);}//当行数小于7时；递归调用下一行else{print();}//调用输出函数flag[col]=true;//回溯d1[n-col+7]=true;d2[n+col]=true;}}return number;
}
int main()
{
number=queen(0);//从第0行开始执行
printf("共有%d种摆放方法",number);//输出方法的个数return 0;}

利用递归回溯的方法来解决八皇后问题的程序步骤较少且可读性强，代码量少，不用尝试所有错误的摆放方法，遇到错误就回溯，效率较高。但递归算法占用空间更大，且每调用一次函数都要在内存栈中分配一定的空间，而栈的空间是有限的，若递归调用的层次太多就容易造成栈的溢出。

2 回溯法（非递归）

位置冲突算法：建立一个一维数组a[9]（a[0]不用）,a[1]~a[9]八个数分别代表棋盘的一行，其中的数值代表该行皇后所在的列数，若任意两个数的数值相等则表明在同一列（冲突），若任意两个数所在的行数差值的绝对值等于列数的差值的绝对值（在同一对角线上冲突）

#include <stdio.h>
#include <math.h>bool Chongtu( int a[], int n) {int i = 0 , j = 0 ;for (i = 2 ; i <= n; ++i)          
for (j = 1 ; j <= i- 1 ; ++j)              
if ((a[i] == a[j]) || (abs(a[i]-a[j]) ==abs(i-j)))//1：在一列；2：在对角线上。每一行都要与前面所有行进行判断是否冲突return false ;   //冲突return true ;} //不冲突
//八皇后问题：迭代法（回溯）
void Queens8(){int n = 8 ;        //8个皇后int count = 0 ;//记录当前第几情况int a[ 9 ] = { 0 };   //存放皇后位置，(第0行0列不用，便于直观看出皇后位置)int i = 0 ,k = 1 ;  //初始化k为第一行a[ 1 ] = 0 ;     //初始化a[1] = 0while (k > 0 )    {a[k] += 1 ;    //a[k]位置，摆放一个皇后while ((a[k] <= n) && (!Chongtu(a,k))) //如果a[k]（即皇后摆放位置）没有到k行最后，且摆放冲突。a[k] += 1 ; //将皇后向后移一位直至不冲突或a[k]>n超出范围则结束循环if (a[k] <= n) //皇后摆放位置没有到达该行最后一个位置{if (k == n) //8行皇后全部摆放完毕
{
printf( "第%d种情况：\n" ,++count);for (i = 1 ; i <= n; ++i) //打印该种摆放方法情况{for (int j=1;j<=8;j++)		
{    	
if (j!=a[i])		
{   
printf("0|");}else{printf("1|");}}
printf("\n");}
printf("\n");}else      //皇后还未摆放完毕{k += 1 ;    //继续摆放下一行a[k] = 0 ;  //此行初始化a[k] = 0;表示第k行，从第一行开始摆放皇后}}else  //回溯：当a[k]>8进入else,表示在第k列中没有找到合适的摆放位置k -= 1 ; //回溯到k-1步：k表示第几个皇后，a[k]表示第k个皇后摆放的位置}return ;
}
//主函数
int main()
{Queens8();return 0 ;
}

回溯法实质上是利用迭代实现递归回溯的方法，该方法运行效率高，但是代码量更大也更加复杂。

3 枚举法（1）

枚举法即列举出所有摆放方法（无论是否冲突），当八个皇后摆放完毕后再判断该方法是否合理。
冲突算法与回溯（非递归）法相同

#include <stdio.h>
#include <math.h>bool Chongtu( int a[], int n) //判断皇后是否冲突的函数
{int i = 0 , j = 0 ;for (i = 2 ; i <= n; i++) //i：皇后的位置for (j = 1 ; j <= i- 1; j++) //j：皇后的位置if ((a[i]== a[j]) || (abs(a[i]-a[j]) ==abs(i-j))) //1：在一列；2：在对角线上。每一行都要与前面所有行进行判断是否冲突{return false ;} //冲突return true ;}//不冲突
void Queens8()//枚举
{int a[ 9 ] = { 0 }; //用于记录皇后位置：(第0行0列不用，便于直观看出皇后位置)。int i = 0 ,count = 0 ;  
//枚举出八个皇后摆放位置的所有情况
//利用八重循环列举出所有方法并逐一验证for (a[ 1 ] = 1 ; a[ 1 ] <= 8 ; ++a[ 1 ])for (a[ 2 ] = 1 ; a[ 2 ] <= 8 ; ++a[ 2 ])for (a[ 3 ] = 1 ; a[ 3 ] <= 8 ; ++a[ 3 ])for (a[ 4 ] = 1 ; a[ 4 ] <= 8 ; ++a[ 4 ])for (a[ 5 ] = 1 ; a[ 5 ] <= 8 ; ++a[ 5 ])for (a[ 6 ] = 1 ; a[ 6 ] <= 8 ; ++a[ 6 ])for (a[ 7 ] = 1 ; a[ 7 ] <= 8 ; ++a[ 7 ])for (a[ 8 ] = 1 ; a[ 8 ] <= 8 ; ++a[ 8 ])
{	
if (!Chongtu(a, 8 )) /*调用判断该种摆放方法是否冲突的函数，
若冲突则枚举下一种方法，若不冲突则记录此种摆放方式	*/{continue ;}else {							
printf( "第%d情况：\n" ,++count);for (i = 1;i<= 8 ;i++){for (int j=1;j<=8;j++){if (j!=a[i]){printf("0|");}else{printf("1|");}}printf("\n");}//打印该种摆放方法
printf( "\n" );}}
}
int main()//主函数
{Queens8();return 0 ;
}

枚举法思路和代码都简单易懂，但程序的计算量大，方法较基础。

4 枚举法（2）

枚举法（2）的冲突算法及思路与枚举法（1）类似，该方法虽然简化了部分代码，但是时间复杂度更大。（大家可以对照着枚举法1理解我就没加注释了）。

#include <stdio.h>
#include <math.h>
int count = 0;//记录方法次数//输出函数
void showAnswer(int *queen){int i,j;
count++;
printf("第%d种解法:\n",count);
for(i = 0; i < 8; ++i)
{for(j = 0; j < 8; ++j){if(queen[i] == j)printf("1|");elseprintf("0|");}printf("\n");
}printf("\n");}
//判断是否皇后位置是否冲突算法
void chongtu(int *queen){int i,j,flag=1;for(i = 0; i < 8; ++i){for(j = 0; j < 8; ++j){if(i != j){if(queen[i] == queen[j]){flag = 0;}else if(abs(queen[i] - queen[j]) == abs(i-j))flag = 0;}}}if(flag == 1){
showAnswer(queen);//若该方法可行则调用输出函数
}}
//枚举出所有摆放方法（相较于枚举法（1）简化了八重循环）
void set_queen(int *queen)
{int i,flag;while(queen[8] != 1){++queen[0];for(i = 0;i<8; ++i){if(queen[i]==8)            {   queen[i]=0;{ ++queen[i+1];}}}flag =1;chongtu(queen);//摆放后调用位置冲突算法}
}
int main()
{int queen[9] = {0};set_queen(queen);return 0;
}