一、内联函数产生的意义

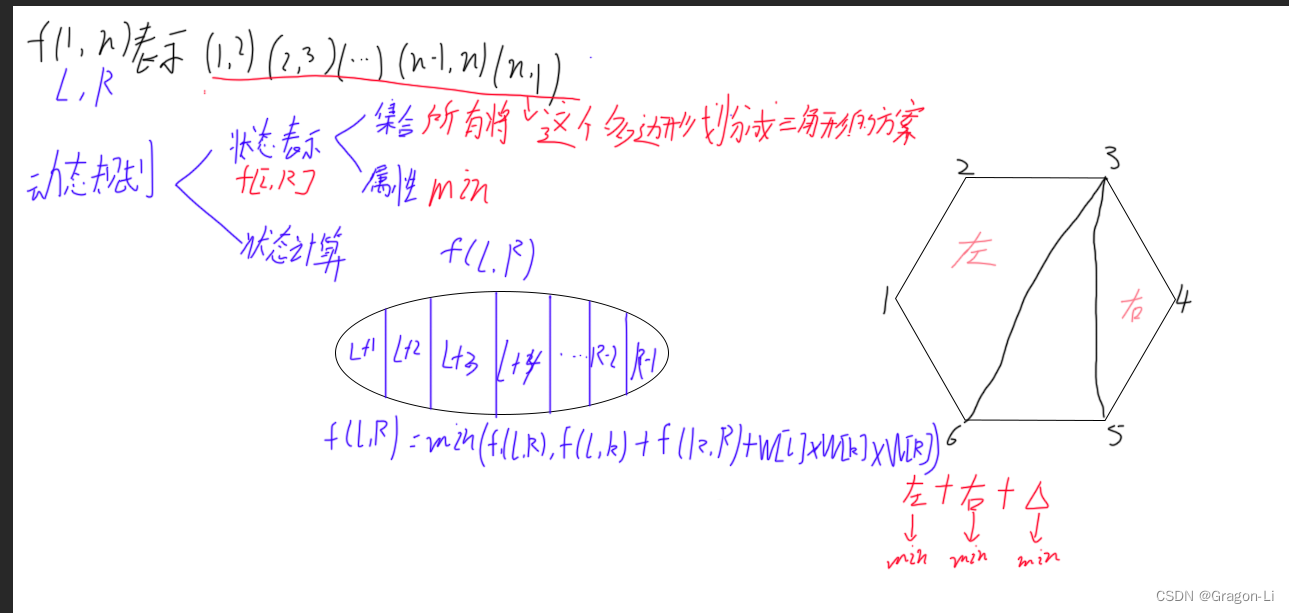
 在C语言中，如果我们频繁调用某些函数，并且这些函数都很代码量都很小，那么写成宏定义的形式无疑是更优的选择，它可以很好的减少函数调用的开支。但是写一个宏对于初学者是一个挑战，对于学习完C语言而不常使用宏的人来说也是一个挑战，所以内联函数的出现就是为了解决C语言中宏定义艰涩难懂的问题。当然它还有其他的优点，我们在下文中会介绍到。

---

二、内联函数的使用

 C++提供inline关键字来定义内联函数：

inline int Add(int a, int b)
{return a + b;
}

---

三、内联函数的作用

①简单易懂

 内联函数的定义只需在函数名前加上inline关键字即可

②支持调试

 我们都知道宏定义是不支持调试的，因为它本质上是一个文本替换，在预处理的时候就被展开了，而调试是在链接完毕，生成可执行程序的时候才进行的。
 那为什么内联函数支持调试呢？这与它的特性有关。

• 在DeBug模式下不会展开，和普通函数没有差别
• 在Release版本下会像宏一样展开，提高效率

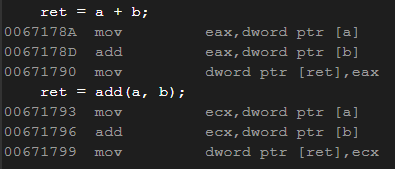
 我们通过观察汇编代码来论证上面的结论：

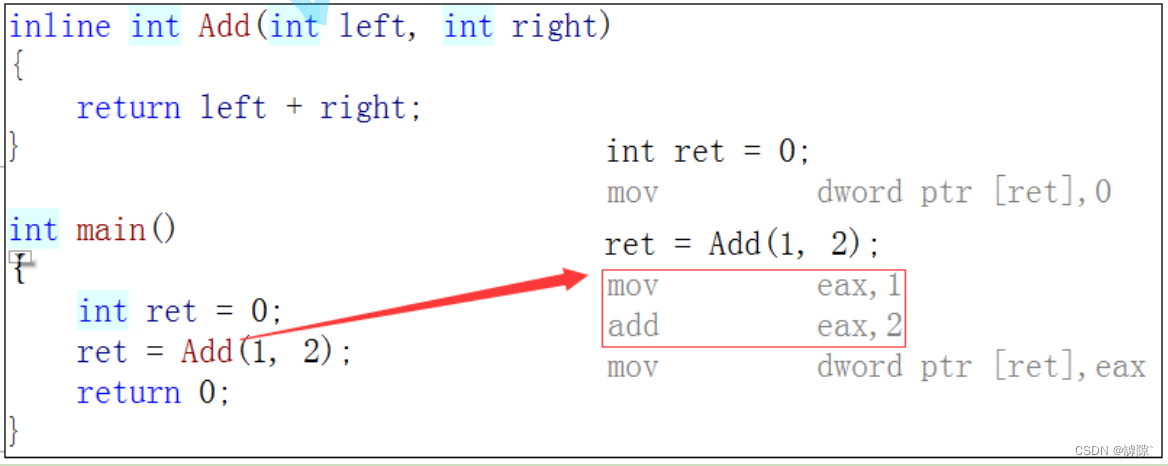
 在release版本下我们看不到call（调用函数）的指令，而是被直接展开处理，即红色方框中的内容

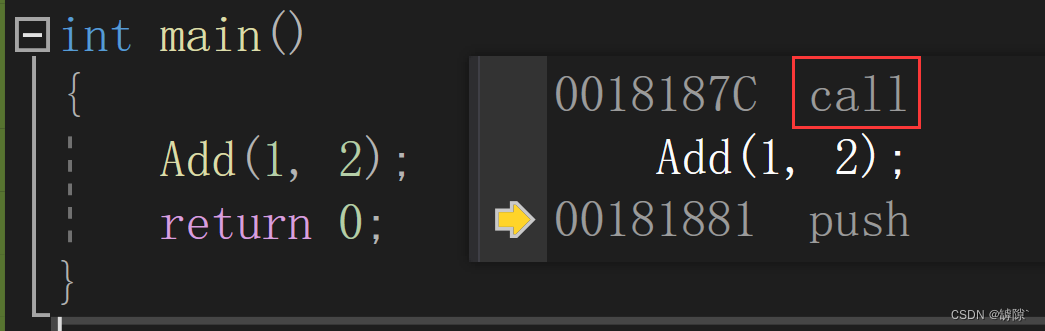
 而在DeBug版本下，我们可以观察到call指令，说明发生了函数调用

③支持类型检查

 在DeBug模式下，内联函数与普通函数没有差别，所以可以进行类型检查

四、内联函数的特性

1. 内联函数是一种以空间换时间的策略，可以减少调用函数的额外时间开销，但将各处内联函数展开增加了实际代码量，从而也就增加了空间的开销
2. 内联函数只是一种建议，执不执行取决于编译器的判断，如果内联的函数过长，那么编译器只会将它当做普通函数处理，并不会展开
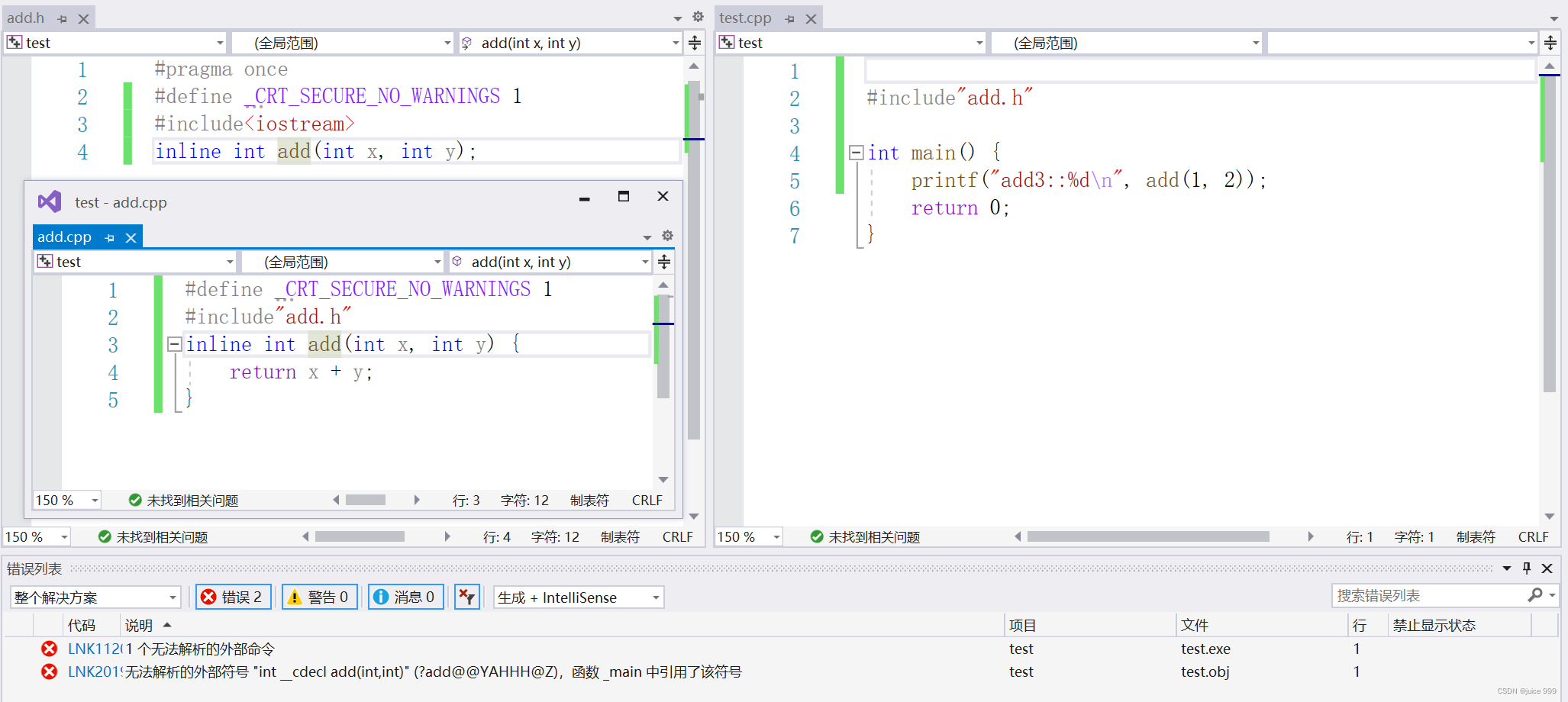
3. 内联函数不能将声明与定义分离。因为在release版本下，内联函数在预处理阶段被展开，在汇编阶段就不会被添加到符号表中去，因此在链接的时候检测不到相应的函数名，就会发生链接错误。