根据百度百科的讲解：

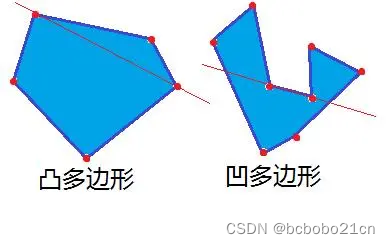
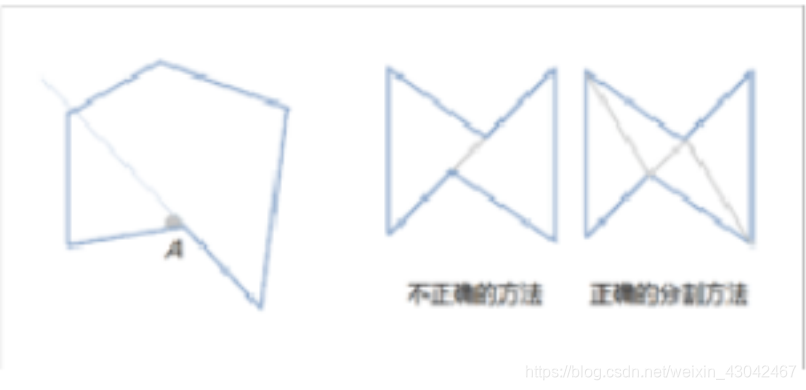
凸多边形

 

现在重点讲解顶点凹凸性法（最常用也是较为简单的方法）：计算总结在最后。

 

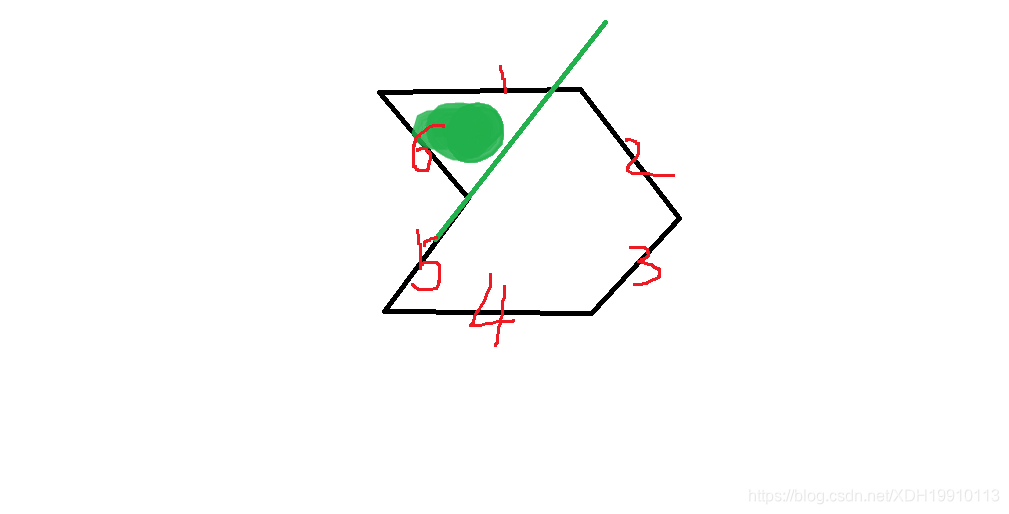
利用向量叉乘的相关知识进行计算：假设当前连续的三个顶点分别是P1，P2，P3。计算向量P1P3,P1P2的叉乘，也可以计算三角形P1P2P3的面积，得到的结果如果大于0，则表示P2点在线段P1和P3的右侧，此时P2对应的角度小于180。然后依次计算下一个前后所组成向量的叉乘，如果在计算时，出现负值，则此多边形时凹多边形，如果所有顶点计算完毕，其结果都是大于0，则多边形时凸多边形。

 

（1）先要知道三角形面积正负的判断

如上图，三角形ABC和三角形ABD。

三角形ABC用叉乘来计算的话，是正的。

三角形ABD用叉乘来计算的话，是负的。

 

（2）关于向量叉乘的坐标运算：

如果是在二维直角坐标的时候，相当于u3=0，v3=0

也就是

所以关于叉乘最后的结果，如果是正的，说明对应的三角形面积为“正”，也就是对应的为凸的。如果为“负”，也就是为凹的。

 

（3）叉乘的正负和多边形的凹凸性关系

把多边形找出固定一个点为P1，然后按给的点顺序设为P2和P3。也就是P1是固定的点，但是P2和P3对应会变的

P1P3=(x3-x1,y3-y1)和P1P2=(x2-x1,y2-y1)，计算这两个向量的叉乘。

因为是考虑P2在P1P3的左右侧，所以是P1P3先，然后是P1P2

也就是

记忆：xy-yx，然后数字就是反过来，本来下标是1312，所以反过来就是2131 2131

这样子计算，如果是正的，说明P2在P1P3的右边，角度小于180，也就是凸的。

如果是负的，说明P2在P1P3的左边，角度会大于180，那就是凹的。

 

（4）判断凹凸多边形

如果全部都是凸的，就是凸多边形；如果出现一个是凹的，那就是凹多边形。

 

（5）计算多边形面积：和凹凸性有关

利用多边形可以定一个点，比如第一个点，然后和剩下的n-1个点组成n-2个三角形，那么这个多边形的面积就是n-2个三角形的面积之和，而三角形的面积可以利用向量叉乘的一半来表示。

那么此时的疑问，向量叉乘是有正负的，那么这个正负有什么印象呢？当三角形的面积为正，表示这部分是凸出去的，因为是正的，那么是加到多边形面积的一部分。若三角形的面积为负，表示这部分是凹进来的，那么相当于这部分的面积是需要少掉的，所以时需要从多表现面积中去掉的一部分。

所以假如所有的点有n个点，用x[0]-x[n-1]和y[0]-y[n-1]表示，那么定一个点，如第一个点x[0],y[0]，然后比如这个点为P1，然后下面就是P1P3和P1P2进行向量叉乘，也就是xy-yx，2131 2131：

即(x2-x1)*(y3-y1)-(y2-y1)*(x3-x1)，而x1,y1其实就是x[0],y[0]。而x2，y2是x[i]，y[i]。x3，y3就是x[i+1]，y[i+1]。

那么就是：((x[i]-x[0])*(y[i+1]-y[0])-(y[i]-y[0])*(x[i+1]-x[0]))/2.0;为面积，如果是凸为正，若是凹为负，就是相加起来。

其中 i 从1到n-2，这样子 i+1 就对应2到n-1，也就全部的点。

 

（6）例子

上面的是，一个凸多边形，我们认为固定O为P1，然后按顺序给P2、P3。根据（1）中可以知道，计算出来的所有三角形面积都是正的，因此面积是所有三角形面积之和，同时面积都是+的，说明都是凸点。

 

上面的是，一个凹多边形，其中A为凹点。

总共有可以分为三个三角形，多边形面积 = 三角形OAB + 三角形OBC + 三角形OCD

其中三角形OAB是 负 的，但是三角形OBC是 正 的，刚好抵消后，就是多边形OABC的面积。

 

因此所有多边形的面积，都是分成了多个三角形的面积之和。（只是由于三角形的面积有正有负—对应凸和凹）

 

要点：

• 使用三个点的向量叉乘，是P1，P2，P3，组成两个向量：P1P3和P1P2，以第一个点为起点P1，然后按顺序设P2和P3。因为是以P1P3为边界考虑P2在哪侧，      顺序取点，值得是对所有点，固定了一个点之后，剩下的点，按逆时针取

所以是P1P3×P1P2，是计算这两个向量叉乘。

• 还有关于向量叉乘的公式，可以推导。也可以记忆，因为是P1P3×P1P2，一定是xy-yx，接着就是反过来，

所以是：2131 2131

• 然后计算结果为正，表示为凸；计算结果为负，表示为凹。只要有凹一定是凹多边形，要全部都是凸才是凸多边形