题目:
给定一个具有 NN 个顶点的凸多边形,将顶点从 11 至 NN 标号,每个顶点的权值都是一个正整数。
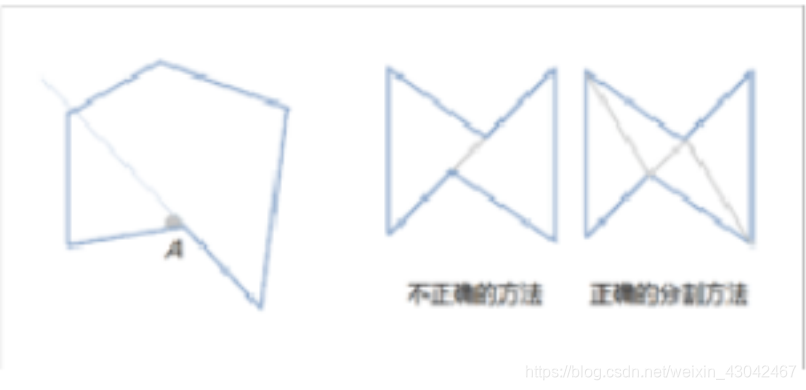
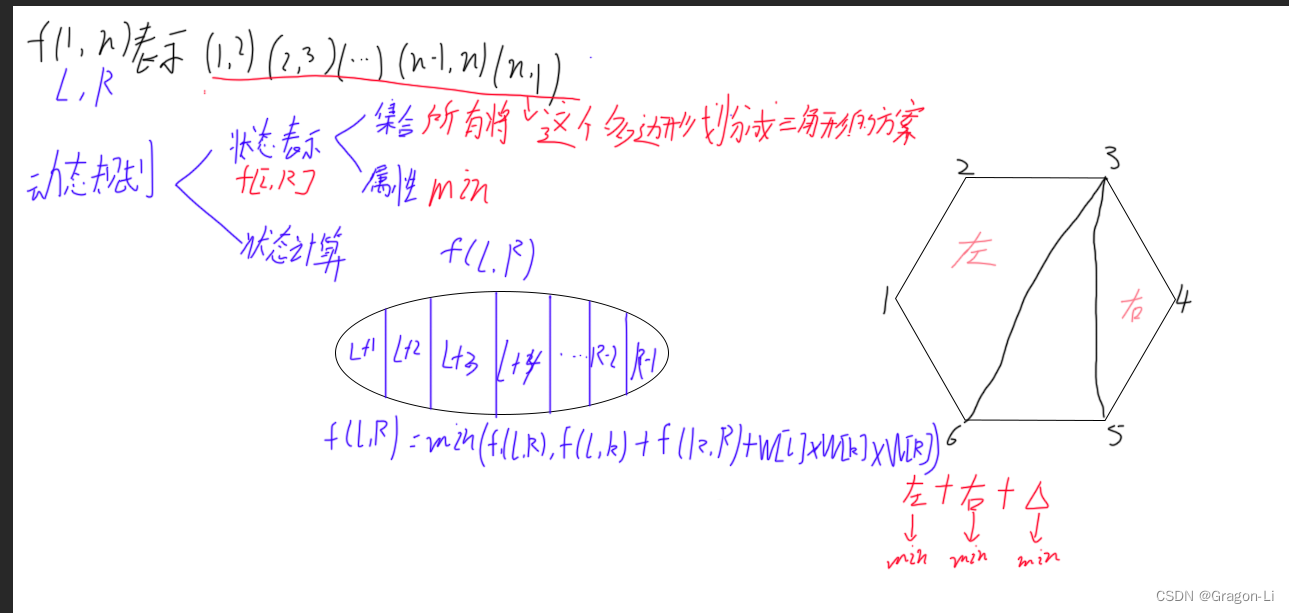
将这个凸多边形划分成 N−2N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 NN,表示顶点数量。
第二行包含 NN 个整数,依次为顶点 11 至顶点 NN 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N≤50N≤50,
数据保证所有顶点的权值都小于10^9
输入样例:
5
121 122 123 245 231
输出样例:
12214884题目来源:《信息学奥赛一本通》
当我们划分区域的时候一次能划分出3个区域将每个区域的最小乘积累加就是当前划分三角形方案的值 然后对所有划分方案取最小值 就是本题的答案
由于本题所有顶点权值都小于10^9次方 3个顶点的乘积必然会超过int的范围 也没有让我们对大质素做模运算 数据规模将会非常大 例如3个10^8相乘=10^24 longlong能支持十进制下大约19位数 所有我们得用高精度进行计算
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 55,M = 35;ll dp[N][N][M];
int w[N];int n;void add(ll a[],ll b[]){static ll c[M];memset(c,0,sizeof c);for(int i = 0,t =0;i<M;i++){t+=a[i]+b[i];c[i] = t%10;t/=10;}memcpy(a,c,sizeof c);
}void mul(ll a[],ll b){static ll c[M];memset(c,0,sizeof c);ll t = 0;for(int i =0;i<M;i++){t+=a[i]*b;c[i] =t%10;t/=10;}memcpy(a,c,sizeof c);
}int cmp(ll a[],ll b[]){for(int i = M-1;i>=0;i--){if(a[i]>b[i]){return 1;}else if(a[i]<b[i])return -1;}return 0;
}void print(ll a[]){int k = M-1;while(a[k] ==0 && k>1)k--;while(k>=0){cout<<a[k--];}
}int main(){cin >> n;for(int i= 1;i<=n;i++){cin >> w[i];}ll temp[M];for(int len = 3;len<=n;len++){for(int l = 1;l+len-1<=n;l++){int r = l + len -1;dp[l][r][M-1]=1;for(int k = l+1;k<r;k++){memset(temp,0, sizeof temp); temp[0] = w[l];mul(temp,w[k]);mul(temp,w[r]);add(temp,dp[l][k]);add(temp,dp[k][r]);if(cmp(dp[l][r],temp) > 0){memcpy(dp[l][r],temp,sizeof temp);}}} }print(dp[1][n]);return 0;
}