为什么要有内联函数

在学习内联函数之前，大家可以写一个实现加法的宏ADD()，检测一下自己。

如果对宏等预编译知识不太熟悉的话，可以先看一下这篇文章：预编译——2.2.4

以下是一个正确的ADD宏：

#define ADD(x,y) ((x)+(y))

灵魂三问：

你在 x 和 y 前面加类型了吗？
x 和 y 都加括号了吗？
整体加括号了吗？

如果以上三个问题都对了，那么恭喜你，宏定义表达式学的还不错

一个简简单单的ADD（），就需要注意这么多问题，可以说宏这个知识点用起来着实是鸡肋，晦涩难懂；

同时宏也是不支持调试的，也没有类型安全的检查。

发明c++的大佬无疑也发现了这个问题，于是引出了内联函数的概念：用函数的语法解决宏的事。

可能兄弟们要说了，直接用函数不就好了？

如果是一个几十行的函数，函数本身执行就很耗时，那调用函数、创建栈帧的一两行可以忽略不计；但是如果一个函数本身就一两行，因为调用函数本身而产生的那一部分消耗，就格外突出，而宏或者内联的提前替换就显得格外优秀，提高了效率。

内联函数

语法

只需要在函数的最前面加一句 inline ，如下：

inline int add(int a, int b)
{return a + b;
}

概念

以 inline 修饰的函数叫做内联函数，编译时C++编译器会在调用内联函数的地方展开，没有函数压栈的开销，内联函数提升程序运行的效率。

inline int add(int a, int b)
{return a + b;
}
int main()
{int ret = 0, a = 1, b = 2;ret = a + b;ret = add(a, b);
}

为了观察内联函数的调用方式，我们看一下汇编代码：

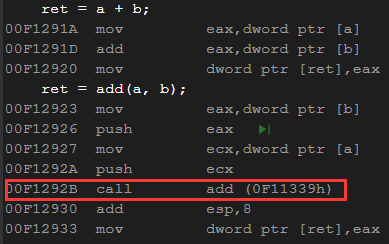
这是Debug模式下main函数的汇编代码。

可以发现 call add (0EA1465h)这一句其实是在调用函数，但是如果按照开始的定义，既然直接展开了，那就不会有调用函数这一步。

这是因为Debug模式下，为了调试方便，编译器默认不进行优化，也就是不会展开，依然使用一般函数的调用方式。

以下，在VS环境下，打开对 inline 的优化再展示一遍：

设置优化inline ：

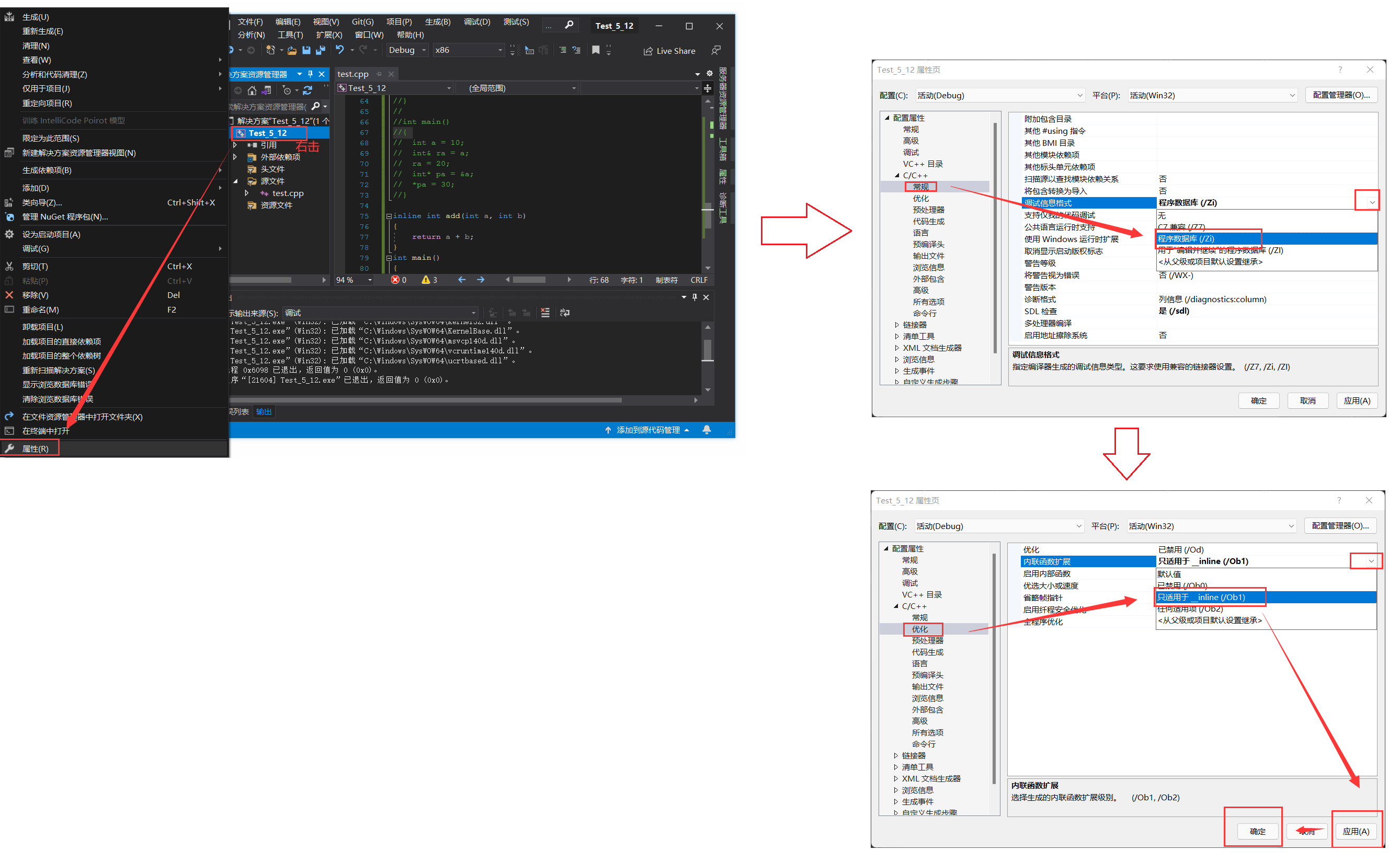
优化后的汇编代码：

（注：汇编代码的打开方式：F10或Fn+F10进到调试模式–>对任意语句右键–>转到反汇编）

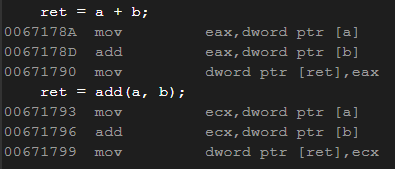
可以看到，优化之后inline修饰过的函数会直接展开。

也就是说，在Debug模式下你写代码、调试代码时，inline 相当于普通函数，可以进行调试；在release模式下，又可直接进行原地展开，提高效率（这里指的是避免了调用函数、创建栈帧等方面的资源消耗）

特性

inline是一种以空间换时间的做法，省去调用函数、建立栈帧的额外开销；
但是如果代码很长（一般是10行左右，具体取决于编译器），或者有递归函数，就不适宜使用递归函数。
inline对于编译器而言只是一个建议，编译器归自动优化，如果定义的函数很长或者递归函数等等，编译器优化时会忽略掉内联。
inline不建议声明和定义分离，分离会导致链接错误。因为inline被展开，就没有函数地址了，链接就会找不到。
测试：
F.h
```
#include <iostream>
using namespace std;
inline void f(int i);
```
F.cpp
```
#include "F.h"
void f(int i)
{cout << i << endl;
}
```
main.cpp
```
#include "F.h"
int main()
{f(10);return 0;
}
```
报错：

error LNK2019: 无法解析的外部符号 “void __cdecl f(int)” (?f@@YAXH@Z)，函数 _main 中引用了该符号

分析：
首先把.h中的内容替换到.cpp中，替换之后
F.cpp
```
#include <iostream>
using namespace std;
inline void f(int i);
void f(int i)
{cout << i << endl;
}
```
在编译过程中，编译器一看，这里的 f() 是个inline，

inline就是说，“我”在调用的地方已经展开了，那么还需要这个给函数一个地址吗？不需要。

也就说F.cpp生成的符号表中，不会有f()的地址。

然后一链接，main.cpp中的 f(10)； 就要去F文件给过来的符号表找 f() 的地址，找不到就会报链接错误。

(注：如果大家对编译链接的知识感兴趣，可以看一下这篇文章：点我)

改正：

那怎么写呢？

不在F.cpp中写这个函数的定义，直接把声明、定义（可以只有定义，更香）都放到 F.h 中去，预编译阶段会直接把内联函数换到main.cpp，相当于在main.cpp头顶上定义了这个内联函数，编译阶段就直接在调用的地方被展开。
F.h
```
#include <iostream>
using namespace std;
void f(int i)
{cout << i << endl;
}
```
main.cpp
```
#include "F.h"
int main()
{f(10);return 0;
}
```

知识大总结

宏的优缺点：
- 优点：
  1. 增强代码的复用性。
  2. 提高性能。
- 缺点：
  1. 不方便宏调试（因为预编译就进行了替换）
  2. 导致代码可读性变差，可维护性变差，容易误用。
  3. 没有类型安全的检查。
C++有哪些技术替代宏：
1. 常量定义——换用const
2. 函数定义——换用内联函数

：
- 优点：
1. 增强代码的复用性。
2. 提高性能。
- 缺点：
1. 不方便宏调试（因为预编译就进行了替换）
2. 导致代码可读性变差，可维护性变差，容易误用。
3. 没有类型安全的检查。