【编程题】判断一个多边形是否为凸多边形

article/2025/9/18 10:17:05

题目：
顺序输入点的坐标，判断按这些点顺序连接起来的多边形是否为凸多边形还是凹多边形

输入描述：

输入包括两行；
第一行是一个整数n，n>=3，作为提示输入的顶点数量
第二行为2*n个整数，为各点的(x,y)

输出描述：

若为凸多边形，则输出为“这是凸多边形”
若不是凸多边形，则输出为“这不是凸多边形”

解析：
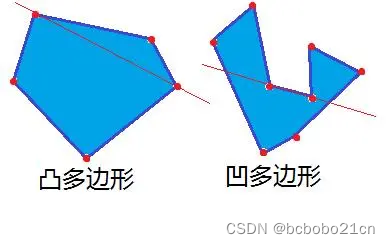
对于凸多边形有：
每个内角都为小于180度的角，没有大于180度的角。

解法1：
对于一个凸多边形，其每个顶点较小的角的和必为其边长减2再乘以180度：（n-2）*180
对于一个凸多边形，其每个顶点较小的角的和必小于其边长减2再乘以180度：（n-2）*180
在这里插入图片描述
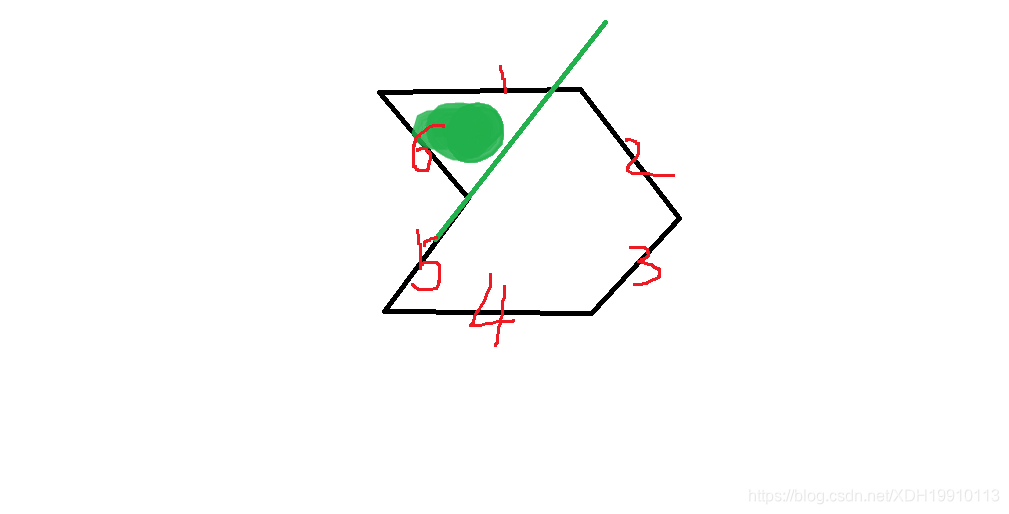
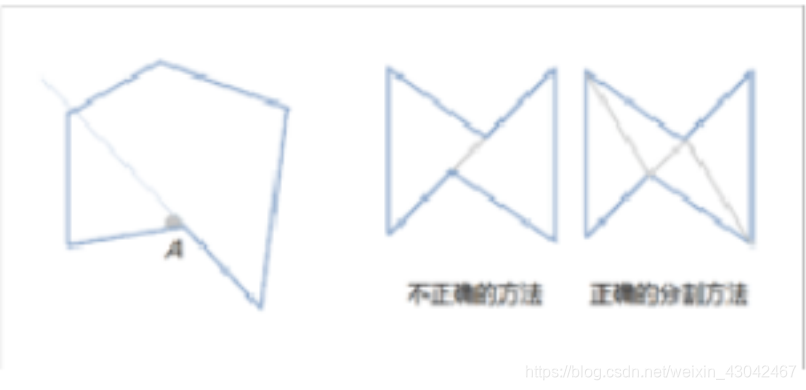
对于凹多边形afbcd，对应的凸多边形aebcf，顶点f和顶点e所在角的较小角相等，可见相比凸多边形，凹多边形顶点较小角和缺少角eaf与角ebf

代码：

#include <iostream>
#include <vector>
#include <cmath>using namespace std;#define PI 3.1415926535897//获取角度
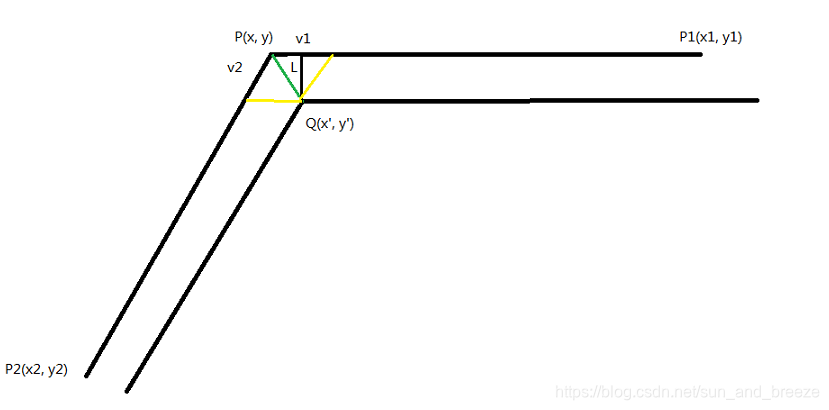
//其中（x1，y1）、（x3，y3）是角的两端，（x2，y2）是角的顶点
double get_angle(int x1,int y1,int x2,int y2,int x3,int y3)
{float v1_x = x1 - x2;float v1_y = y1 - y2;float v2_x = x3 - x2;float v2_y = y3 - y2;float t = (v1_x * v2_x + v1_y * v2_y) / (sqrt(pow(v1_x, 2) + pow(v1_y, 2)) * sqrt(pow(v2_x, 2) + pow(v2_y, 2)));float ans = acos(t) * (180 / PI);//cout << "角为：" <<ans << "度" << endl;return ans;
}
int main()
{int n;cin >> n;//为凸多边形时应为的总度数double angle_sum = (n - 2) * 180;//可以做一个点类//坐标x与y的数组vector<int> arr_x, arr_y;//读入for(int i=0;i<n;i++){int x, y;cin >> x >> y;arr_x.push_back(x);arr_y.push_back(y);}//实际较小较内角和double sum = 0;//陆续读入各角for(int i=0;i<n;i++){//需要判断第0个角和最后的一个角if(i==0){sum += get_angle(arr_x[n - 1], arr_y[n - 1], arr_x[i], arr_y[i], arr_x[i + 1], arr_y[i + 1]);}else if(i==n-1){sum += get_angle(arr_x[i - 1], arr_y[i - 1], arr_x[i], arr_y[i], arr_x[0], arr_y[0]);}else{sum += get_angle(arr_x[i - 1], arr_y[i - 1], arr_x[i], arr_y[i], arr_x[i + 1], arr_y[i + 1]);}}///判断if(sum<angle_sum){cout << "这不是凸多边形" << endl;}else{cout << "这是凸多边形" << endl;}
}

注：
实际上，由于计算机对于浮点数的存储是近似存储，在做浮点数的比较时可能出现误差的情况。

解法2：
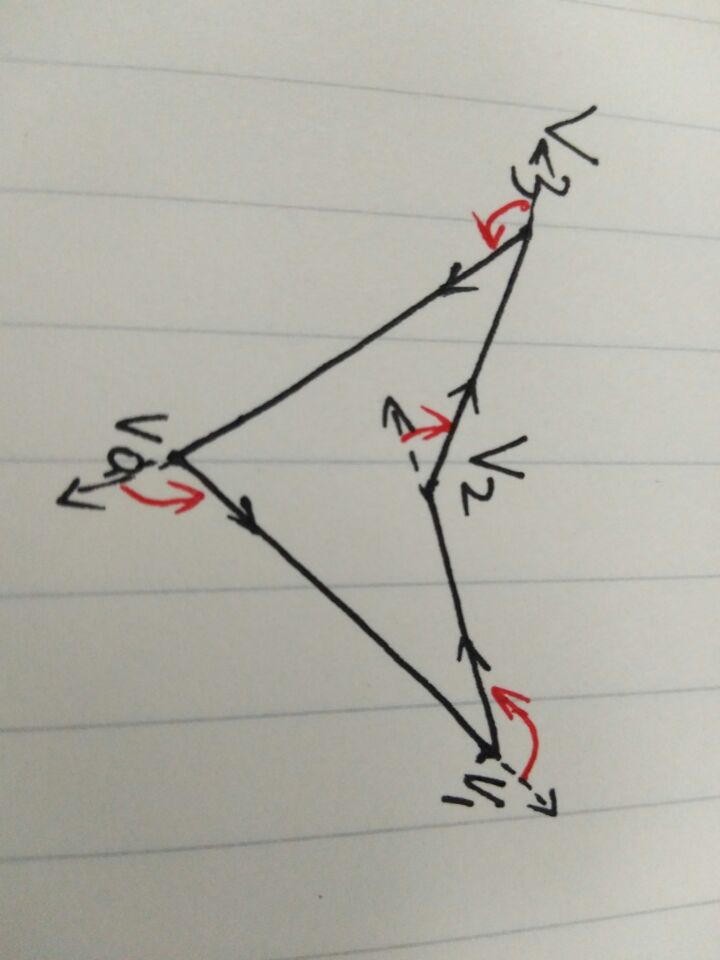
如果把多边形的边顺序按同一侧作为起点来看，可以发现，凸多边形的边都按同一角度选择着
根据这一规律，我们对边的向量进行叉乘，便可判断

以下参考：https://www.cnblogs.com/wmxl/p/5294620.html
向量的叉乘如X叉乘Y就是一个垂直与X和Y组成的平面的一个向量，方向是这样决定的，右手四指与X的方向相同，大拇指与四指垂直,然后四指按照这样的方向绕，从X开始,经过X与Y的锐角的方向环绕,拇指所指的方向就是X叉乘Y的方向
在这里插入图片描述
叉乘是三维才有意义, 这里虽然是二维的, 但可以看成第三维z是0
所以计算结果就变成了(0, 0, x1y2 - x2y1)

叉乘的几何意义是一个垂直于两个向量的方向, 如果所有边依次相乘的方向都是一样的, 就是凸多边形, 此题因为规定了必须逆时针, 所以所有相乘都必须是正的(这个可以自己试一下就知道)

代码：

#include <iostream>
#include <vector>using namespace std;int main()
{int n;cin >> n;//可以做一个点类//坐标x与y的数组vector<int> arr_x, arr_y;//读入for(int i=0;i<n;i++){int x, y;cin >> x >> y;arr_x.push_back(x);arr_y.push_back(y);}//这次用的是向量，为了方便求最后一组向量，直接把点0，点1再次压入，arr_x.push_back(arr_x[0]);arr_y.push_back(arr_y[0]);arr_x.push_back(arr_x[1]);arr_y.push_back(arr_y[1]);bool flag = true;//判断各向量for(int i=0;i<n;i++){//向量1int v1_x = arr_x[i + 1] - arr_x[i];int v1_y = arr_y[i + 1] - arr_y[i];//向量2int v2_x = arr_x[i + 2] - arr_x[i+1];int v2_y = arr_y[i + 2] - arr_y[i+1];//叉乘//小于0为凹多边形if(v1_x*v2_y-v2_x*v1_y<0){flag = false;break;}}if(flag){cout << "这是凸多边形" << endl;}else{cout << "这不是凸多边形" << endl;}
}