什么是内联函数(Inline Function)

内联函数是给编译器的提议，在编译成汇编代码时，直接将函数的代码语句在调用处展开，用于优化程序的运行效率。若函数体代码过长或因其他原因不适合内联，编译器可能不接受内联提议，按照普通的函数规则编译。

如何将函数编写为内联函数（how to make function inline）

在函数声明或者定义前加上inline即可。

例：

//不是内联函数
int add1(int x, int y) {return x + y;
}
//内联函数
inline int add2(int x, int y) {return x + y;
}
//内联函数
int add3(int x, int y);
inline int add3(int x, int y){return x + y;
}
//内联函数
inline int add4(int x, int y);
int add4(int x, int y){return x + y;
}
//内联函数
inline int add5(int x, int y);
inline int add5(int x, int y){return x + y;
}

为什么使用内联函数（Why to use inline function）

例有代码如下：

#include<stdio.h>
int add1(int x, int y) {return x + y;
}
inline int add2(int x, int y) {return x + y;
}
int main() {printf("add1::%d\n", add1(1, 2));printf("add2::%d\n", add2(1, 2));return 0;
}

add1普通的函数，add2 为内联函数。这段代码的运行结果为：

那add1和add2他们的区别是什么呢？

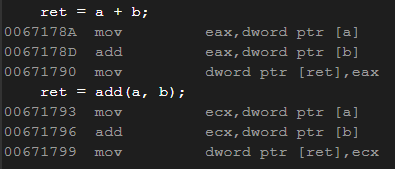
在调试时转到反汇编：

结论：

故当一个函数同时满足：

1.需要被反复调用

2.函数体本身简短

我们可以考虑将它编写为内联函数，以节省开辟栈帧的开销，优化运行效率。

相反，若函数体本身较长，或者调用次数很少，那么这种空间换时间的操作就显得没有必要了。

特殊规则

1.编译器可能不接受内联提议

前面提到过内联只是给编译器的提议，若编译器判断当前函数不适合内联（如包含递归，函数体过长等等），便会将它当成普通的函数进行编译。

例子：

#include<stdio.h>
inline int add3(int x, int y) {int a = 0;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;a++;return x + y;
}
int main() {printf("add3::%d\n", add3(1, 2));return 0;
}

反汇编：

2.内联函数的定义和声明不可分离于不同文件

内联函数的声明和定义不能分离在不同的文件，会导致链接错误，但是以下两种情况除外：

1.调用内联函数的函数与内联函数，它们的定义在同一个文件；
2.编译器没有选择将代码展开（如代码长的情况）；

总之将内联函数的定义声明分离时及其危险的，一般将内联函数的定义和声明都放在同一个源文件或者头文件中，以防止出错。

错误示范

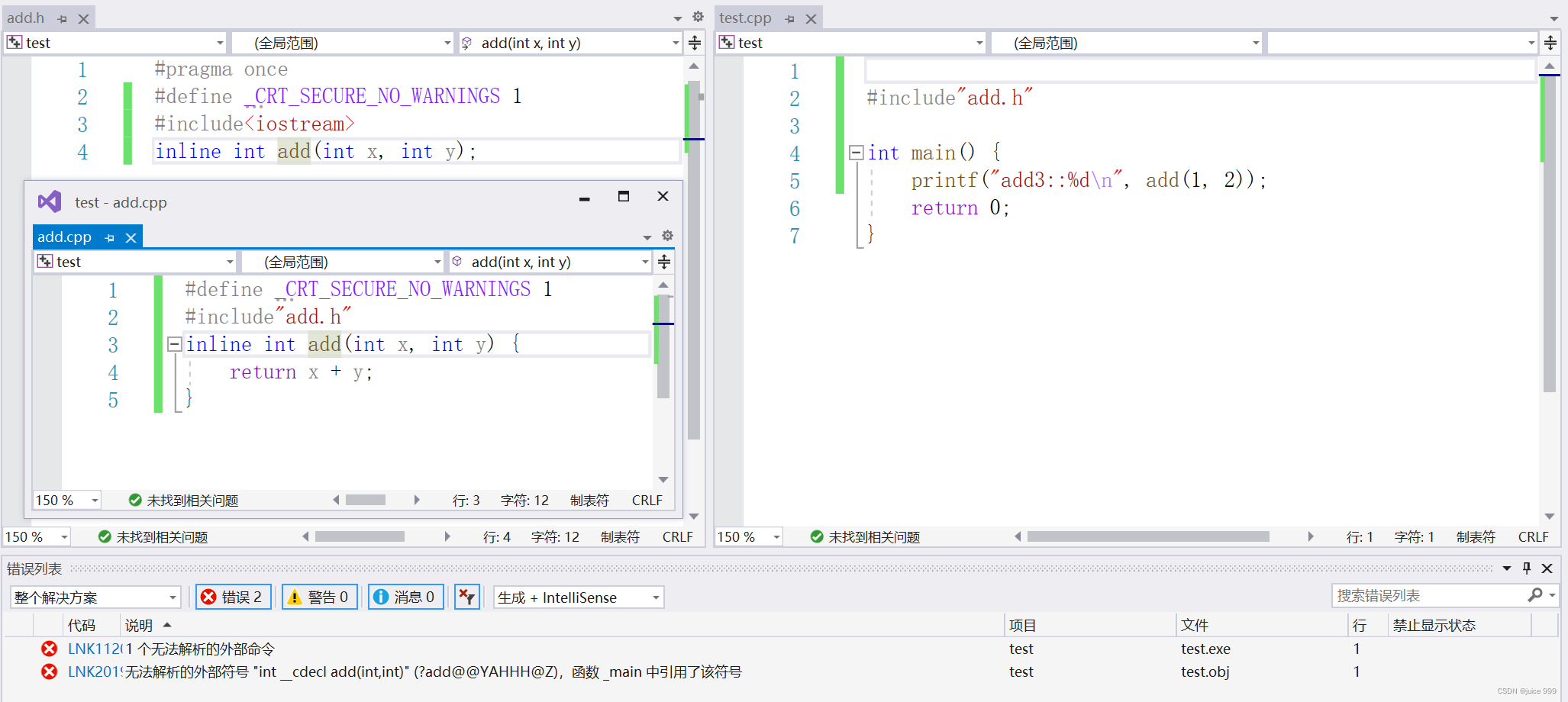
正确示范：

//内联函数
inline int add2(int x, int y) {return x + y;
}
//内联函数
int add3(int x, int y);
inline int add3(int x, int y){return x + y;
}
//内联函数
inline int add4(int x, int y);
int add4(int x, int y){return x + y;
}
//内联函数
inline int add5(int x, int y);
inline int add5(int x, int y){return x + y;
}