目录
基本概念
证明思路
常见例子
21个常见NPC问题
原理论证
基本概念
P类问题:(polynominal) 存在多项式时间算法的问题,即在多项式时间内可解的问题;
例如:冒泡排序、快速排序等问题;
NP类问题:(Nondeterministic polynominal) 能在多项式时间内验证出一个正确解的问题,也就是说这个问题不一定在多项式时间内可解,但可以在多项式时间内验证;
例如:大数分解问题,比如180576这个数让你拆成两个数相乘,必须是三位乘以三位的,可能很久都解不出来(如果是一个很大很大的数的话),但是我告诉你这是352*513得到的,那么很简单就能在多项式时间内验证是否正确,这就是NP问题;
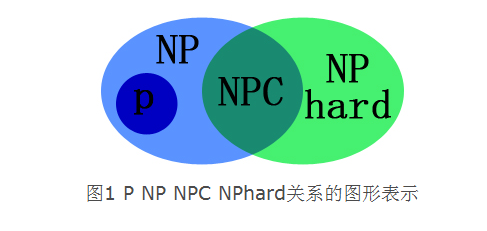
NPC类问题(Nondeterminism Polynomial complete):存在这样一个NP问题,所有的NP问题都可以约化成它。
NP-Hard类问题(Nondeterminism Polynomial hard):所有的NP问题都可以约化成它。
这里插一句,何为约化,以及两者的具体解释我在下面给出,但是可以看的所谓的NP完全问题和NP难问题的唯一差别就是这个问题本身是不是NP问题。然后两者都是可以被所有NP问题约化的。那也就是说,NP-H问题是包含NPC问题的,而NPC又至少是一个NP问题,那么它也被NP包含,但NP-H问题不一定是NP问题,所以有一部分NP-H问题是NP,有一部分不是,这样整个概念相互包含与相交的逻辑就出来了,如下:

因此说了这么多,个人认为为什么要判断一个问题是哪类问题,原因在于,它有助于让我们在决心实现这类问题之前对问题的难易程度进行一个有效的判断。如果一个问题是一个NP难问题,众所周知我们是不一定能够找到最优解的,有时候持有次优解即可。如果一个问题连NP问题都不是,也就是说我在多项式时间内连验证它都很费劲,又谈何解决出来呢?这类问题就不大有研究的必要了;
证明思路
前面的概念留了一个点,说NP-H问题和NPC问题都是所有NP问题可以约化到的,那么究竟什么是约化?我了解到的:若B能解决A,那么就说A可以约化到B,也就是说,B是一个复杂度比A更高的算法,B通过某种特殊情况(简化),可以变成A问题,比如B问题是二元一次方程,A问题是一元一次方程,当B问题,y=0时,它就转变成了一元一次问题。也就是说B问题能解决A,那么就说A问题可以约化到B;
那说了这么多,NPC的或者NP-H问题的证明思路究竟是什么呢?首先我要先判断一下这个问题本身是不是NP问题(给出一个解能否在多项式时间内验证),然后找到一个已知的NPC问题去约化到这个问题,因为我去验证一个问题,把所有NP问题都约化一遍到我这个问题上不太可能,而NPC问题本身的定义就是所有NP问题可以约化到它,那我拿一个已知的NPC问题,去验证这个NPC问题可以约化到它,即
所有NP问题->已知的NPC问题->亟待解决的新问题;
这样,也就简化了我去验证一个新问题是不是NPC问题的方式;
证明是NP-Complete 问题: 证明是NP-Hard 问题:
①证明本身是NP问题; ①无需证明本身是NP问题;
②证明一个已知的NPC问题能约化到它 ②证明一个已知的NPC问题能约化到它;
常见例子
说了这么多,再来两个例子来巩固一下:

首先是一个诱导子图的问题,问题描述在第一行,那么想证明这个问题是不是NPC问题(是NPC就一定是NP-H了),首先判断它是不是NP问题,那么给出一个子图包含K个点,问你是否最少包含l条边,很容易就能验证,即在多项式时间内可以验证,是NP问题。
其次,找到一个已知的NPC问题,验证这个已知的NPC问题可以约化到这个新问题,那么就能证明他是NPC问题了(即找到一个特殊情况把这个问题简化到已知的NPC问题)
那么当l=时,该问题就变成了找一个K大小的完全子图(因为完全子图边和顶点的关系就是
),而找完全子图的问题也称Clique问题,是一个已知的NPC问题,那么通过设定l的特殊取值,将待解决问题转化成了现有NPC问题,即由一个NPC问题约化而来,本例得证;
2.
In the HITTING SET problem, we are given a family of sets {S1, S2, . . . , Sn} and a budget b, and we wish to find a set H of size ≤ b which intersects every Si , if such an H exists. In other words, we want H∩Si ≠ ∅ for all i.
Show that HITTING SET is NP-complete.
大概的意思就是这是一个碰撞集问题,这个集合H跟Si的各个集合都相交:

然后来证明他是一个NPC问题:
①首先证明它是一个NP问题,像我上图一样,如果给出了一个集合H,问你它是否跟所有的Si都相交,那么这是在多项式时间内可以验证的;即是NP问题;
②证明一个已知的NPC问题可以约化到它:
当我把Si集合特殊化,即我把每条边当成一个Si,集合的元素就是每条边的两端,更改后图如下:
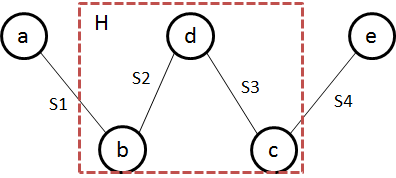
然后把问题变成,找该图中的最小顶点覆盖问题(Vertex cover),即找到的集合包含图中每条边的至少一端。这样也满足了我的集合H和所有Si集合都相交(将Si集合特化成一条边的作用),那么我亟待解决的问题就特化成了已知的NPC问题——最小顶点覆盖问题。那么本例得证;
21个常见NPC问题
既然现有的方式是找到一个已有的NPC问题去验证我要验证的新问题,那么知道了解现有的NPC问题就变得很重要,下面列举了常见的NPC问题,而每个子主题(往后错一格)代表这我可以由前面的主题约化而来:

可以看到,这些问题约化来约化去,都是有一个初始问题的,因为一个问题由另一个已知的NPC问题约化而来,那么第一个NPC问题是怎么来的?那就要用到NPC问题的本身定义了:所有的NP问题可以约化到它;
这个方式就是经典的SAT问题,由上图也可以看到,这些已有的NPC问题它的最开始,都是用SAT问题证明的;
原理论证
证明了所有的算法都是可以编码为boolean formula(布尔型)问题,这意味着所有算法都可以使用SAT去求解,因为他们本质上就是boolean formula问题。
对于任意的boolearn foumula写成以下标准式:
(..∨...∨..)∧(..∨...∨..)∧...
SAT:如何取值,使式子为真?或根本
不存在一个取值使式子为真。
这些话是我做的ppt里写的,直接拷过来,意思就是,这所有算法无外乎就是在一个给定集合中找到解,或者无解,而这些算法的选择,条件等等都是可以编码为布尔型,用合取范式的方式表述这个算法的情况,算法有解,就代表合取范式为真,算法无解,就代表这个式子取值为假。
具体还是看例子,用SAT模型去证明我上面所说的Clique问题:

首先看这个图,我要找它的k=3 的clique也就是完全子图,答案先放在这(b、c、d)
那现在将他编码为布尔型,任意编码,但边代表着我的相邻节点必须可以同时为真,像a,b可以同时取值为X1,X2,但不能同时取值X1和![]() ,然后图就变成下图:
,然后图就变成下图:

编完码后,将其写成SAT的合取范式模型,这里因为k=3,所以合取范式里的析取范式个数为3,搭配是任意的:
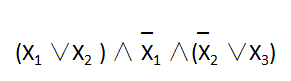
写完后,找到一个k=3的clique,就变成了找到这个合取范式为真的情形。![]() 是单独的,所以它必须为真,那么X1就是假,那X2就必须为真,
是单独的,所以它必须为真,那么X1就是假,那X2就必须为真,![]() 为假,那么X3就必须为真,由此得出,编码bcd为真,即k=3的clique找到了;
为假,那么X3就必须为真,由此得出,编码bcd为真,即k=3的clique找到了;
以上就是NP问题的概念+证明逻辑+例子,当然自己只是浅显的学习,如果有错误或者论证思路不严密,还望赐教;
注:我这里一直再说NPC NPC,因为NPC是包含在NP-Hard问题里的,很多人所讲的这个问题是np难的,其实就是NPC问题,因为NPC比np难多了一个问题本身是NP的,如果这个问题你连验证都验证不了,又谈何解决呢?
![[知识归纳]关于NP问题的概念与解释 | NP-complete NP-hard](https://img-blog.csdnimg.cn/6e74c8ba3a3e4ca9be78afb73d882323.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA5LiBbGluZ2xpbmflk4c=,size_20,color_FFFFFF,t_70,g_se,x_16)