catalog
- 图片引用
- 图二
- 多边形
- 分类
- 周长
- 多边形的外接矩形
- 凸多边形
- 去除若干点, 仍为凸多边形
ID_COUNT: 3
图片引用
图二

多边形
以下讨论, 均在(笛卡尔坐标系)中, 即两点间的距离为 (欧几里得距离)
由N条边和N个点组成, N >= 3, 面积一定> 0
每条边, 都是(线段) 线段: 必须是直的, 不能弯曲
每个顶点, 一定是某两条边的端点;
不可以是(多条边)的端点, 也不可以是两条边的交点(这里的交点, 不是端点)
也就是, 有N条边, 所有的边 两两的 首尾端点连接, 围成一个 封闭的环;
如果给这个环, 一个方向, (顺或逆), 那么, 任意一个点, 入度和出度 均为1
实际上 以下这种多边形定义, 用的多:
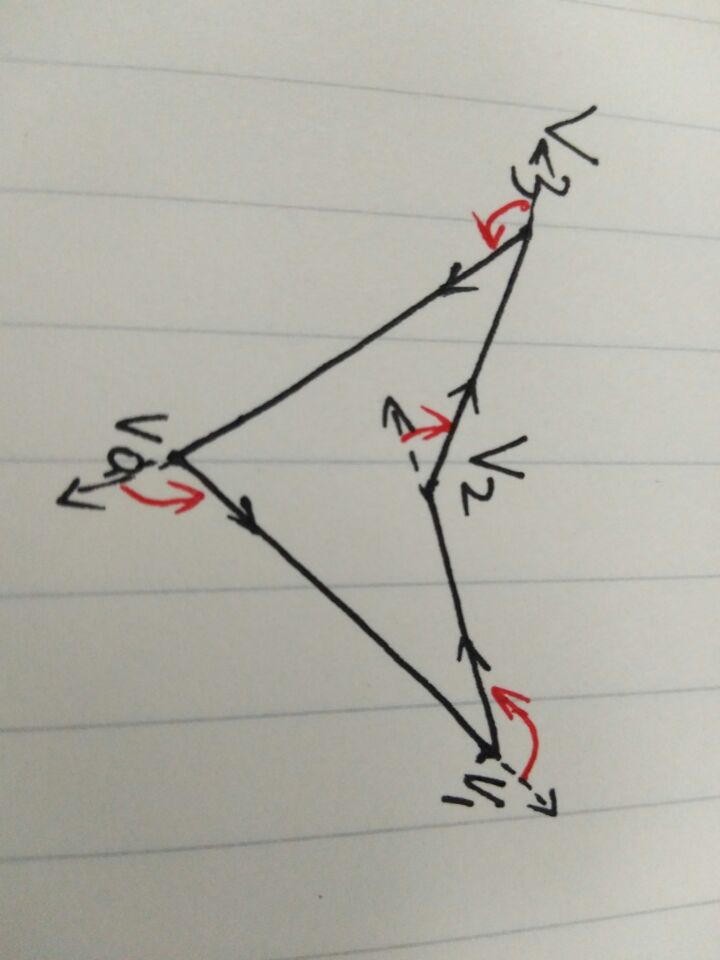
给定N个点v0, v1, v2, ..., 表示多边形(顺/逆时针)的遍历方向,
依次的连接v_i 和 v_i+1端点, 该线段, 就是多边形的一条边;
… 即, 给定N个点的(线性序列), 依次的相邻点连接边, 一共N条边, 就可以唯一的确定一个形状
必须要给定: (顺/逆时针), 这句话; 否则, 其代表的(形状), 不一定是 (多边形)
比如正方形, 从左上角开始, 顺时针方向, 依次记作点为: A B C D;
即, 4个点ABCD 且按照顺时针方向, 就可以唯一的表示这个正方形
但是, 如果不说方向, 单说ABCD四个点, 那么, 如果按照ACBD的方向 去依次连接 去画4条边, 得到一个形状
你会发现, 它都不是多边形
因此, 给定N个点的线性序列时, 一定要提前说明: 该线性序列是有方向的! (顺/逆), 此时, 该线性序列 才可以唯一的表示一个多边形
多边形, 允许三点共线, 即可能会存在 某个角为180;
不管凹/凸边形, 都可能存在 三点共线的情况
分类
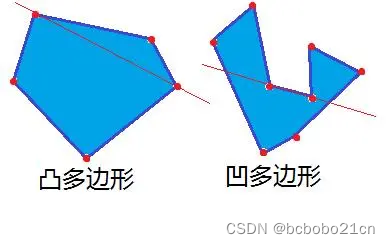
凹凸性
一个多边形, 不是凹多边形, 就是凸多边形
周长
令v0, v1, v2, ..., v(N-1)是该N边形的 按照 顺/逆时针 的所有顶点;
则 周长 = ∑ i = 0 N − 1 D i s t ( i , ( i + 1 ) % N ) 周长 = \sum_{i = 0}^{N - 1} {Dist(i, \ \ (i + 1) \% N)} 周长=∑i=0N−1Dist(i, (i+1)%N)
这个公式的前提是: 所有点是(顺/逆)时针, 如果是乱序 则不成立
… Dist( i, j)是边权; 其定义不是固定的; 可以是(边长, 即欧几里得距离), 可以是(边权, 即用户自定义)
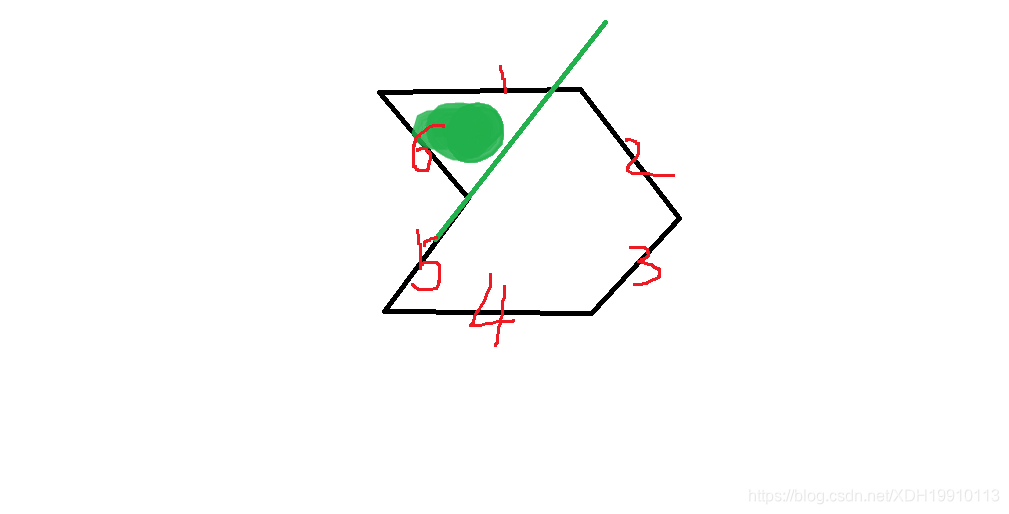
多边形的外接矩形
见图二
任何一个多边形 都存在 唯一的 外接矩形 : 满足 使该多边形处在外接矩形的内部, 且外接矩形最小 (这个小, 可以是周长或面积, 下面会讲到)
图中的8边形(黑色) 的外接矩形为 (绿色矩形).
虽然图中是个凸多边形, 实际上, 对凹多边形也适用, 只要是多边形 都存在 其唯一的(外接矩形)
… 具体的, (求一个多边形的外接矩形的算法) 为: 假设外接矩阵坐标为L, R, U, D
… (LR为矩阵左/右侧边的横坐标, UD为矩阵上/下侧边的纵坐标)
… 令X为多边形所有顶点的横坐标集合X = {x1, x2, ...}, Y为所有顶点的纵坐标
… 则, L = min( X), R = max( X), D = min( Y) U = max( Y)
… 这个算法看起来很简单, 需要牢记住
此时, 这个外接矩形 是有 L, R, U, D 四个数值来表示, 还有一种方式, 来表示这个 外接矩阵
其实和上面的方式差不多, 上面是得到L, R, U, D四个数值, 而这四个值 每个值都来源于一个点
比如, 上图中, L 来自于 A点, U 来自 B点, R 来自 E点 D 来自 H点, 我们就以A, B, E, H这 四个点 来表示外接矩形
表示, A.x, B.y, E.x, H,y 为 L, U, R, D 即外接矩形的四条边的坐标
即, 获得四个点, 记作Vl, Vu, Vr, Vd (V为Vertice), 满足: Vl.x = L, Vu.y = U, Vr.x = R, Vd.y = D (LURD和上面一样)
… 由于对于一个N边形, 只需要这4个点, 就可以完全确定其外接矩形, 其他点可以扔掉不顾
… 因此, 这4个点 也称为extreme point临界点;
以上图为例, Vl = A, Vu = B, Vr = E, Vd = H; 其实和上面表示法差不多;
… 假如, 有多个点 在外接矩形的一条边上, 则取任意一个点即可;
… 比如, 假如G 和 H都在那条绿色边上, 则你选G, H都可以, 因为, 只要保证G/H . y = D即可, 我们只关注其(y坐标), x坐标无所谓
但是要注意, 此时, 这4个点 可能会有重复的!!!
比如, 你想象下, 将A点 移动到 绿色矩形的(左上角), 将 E点 移动到 绿色矩形的(右下角)
然后, 将所有的点, 都放到 绿色矩形的(内部), 不能在边上;
那么, 此时, Vl 和 Vu表示的点 都是A, Vr, Vd表示的点 都是E;
因此下面这种表示外接矩形的方式, 就是为了引入这个知识
即, 多边形的 (2/3/4)个点 可以确定 其外接矩形, 所谓(确定), 就是确定外接矩形的形态/坐标等信息.
… 在外接矩形上即不在矩形内部 的 (多边形点) 可能很多> 4个
… 但是, 只需要最多4个点 就可以确定 外接矩形的形态;
一个N边形
… 如果用2个点可以确定外接矩形, 则说明: 这两个(多边形的点) 位于 (外接矩形)的对角线的两个顶点
… 如果用3个点可以确定外接矩形, 则说明: 某一个(多边形的点) 位于 (外接矩形)的某个顶点
… 然后另外两个(多边形的点), 位于 (外接矩形)的两条边上不在外接矩阵的顶点)
… 否则, 用4个点可以确定外接矩形, 则说明: 这4个(多边形的点) 均位于 (外接矩形)的四条边上 不在外接矩形的顶点
而, 至于 到底是 (2个 / 3个 / 4个) 点 能确实 外接矩阵, 这要看(该多边形)的形态, 也就是上面分析的情况
我们知道, 这4个临界点, 是针对(外接矩形)而言的, 因为矩形有4条边, 所以对应4个临界点;
而, 临界点 可能会重合, 比如, Vl 和 Vu都在 外接矩形的 左上角; 即, 一个多边形上的点, 对应2个临界点 (不会对应>=3, 因为外接矩形面积> 0)
但是, 临界点 它的本质 又是指的是(多边形的点), 因为临界点 一定是 (多边形的点), 不是 ( 外接矩形的顶点)
即, 对Vl, Vu, Vr, VD进行 (去重处理)后, 其点数 是{2 或 3 或 4}
外接矩形的周长: 2 * (R - L) + 2 * (U - D)
凸多边形
定义1: 所有角 均 <= 180
定义2: 将任意一条边延长为直线, 则所有点 要么在该直线上, 要么都在同一侧 (比如在左侧)
… 也有: 所有边 要么在该直线上, 要么都在同一侧(左侧), 不会出现, 某个边与该直线相交 或 在右侧的情况
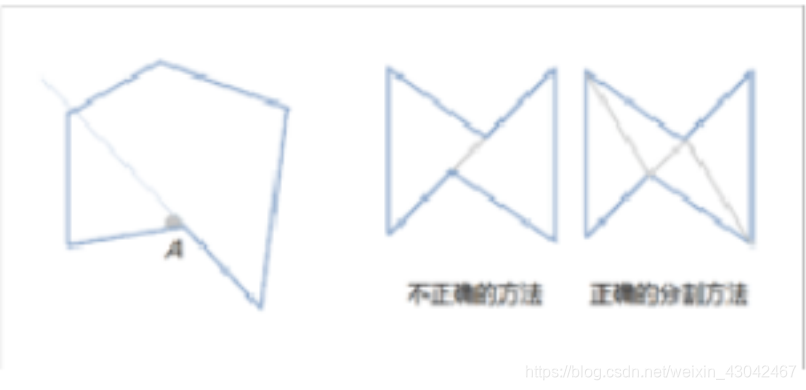
去除若干点, 仍为凸多边形
给定N凸边形 的线性序列: V0, V1, V2, ..., , 其该线性序列是N凸边形的顺/逆时针方向;
则去掉任意一个点后, 假如去掉V2, 则 线性序列V0, V1, V3, ..., 所代表的, 仍然是凸边形, 即N-1凸边形
… 注意, 线性序列是有方向的!! 这是题目一开始就规定好 (或顺或逆), 假如V0, V3, V1, ... 这肯定是不对的
… 比如是点序递增的, 因为点序递增是题目规定的顺/逆时针方向
证明:
从凸边形的定义出发 (延长任意条边, 所有点和边在同一侧),
原来是(N个点 N条边) 在同一侧, 现在是 (N-1个点 N-1条边)在同一侧;
引理, 去掉若干个点后, 线性序列: Vi, Vj, Vz, ... (i < j < z) 仍表示一个 凸多边形;
… 你可以一个个的去点