【学习笔记】Mininet入门实战
课程介绍
Mininet是由一些虚拟的终端节点、交换机、路由器连接而成的一个网络仿真器,它采用轻量级的虚拟化技术使得系统可以和真实网络相媲美。
Mininet可以很方便地创建一个支持SDN的网络:host就像真实的电脑一样工作,可以使用ssh登录,启动应用程序,程序可以向以太网端口发送数据包,数据包会被交换机、路由器接收并处理。
有了这个网络,就可以灵活地为网络添加新的功能并进行相关测试,然后轻松部署到真实的硬件环境中。
本教程将包括入门及实战两部分,让用户通过实操快速掌握Mininet
课程学习
1.1Mininet源码安装与验证
-
以root用户登录主机,以下命令全部以root身份运行。
-
执行ll命令,查看Mininet安装包

- 如果本地没有安装包可以使用网络获取资源
# sudo apt-get update# sudo apt-get install git# git clone http://github.com/mininet/mininet.git
- 查看当前Mininet版本
# cd mininet
# cat INSTALL|more

- 安装Mininet (若使用其它命令安装,在安装前请先执行
apt-get update命令更新软件列表)
# cd util/
# ./install.sh -a
-
测试Mininet的基本功能
mn --test pingall -
查看安装好的Mininet版本
mn --version
安装的时候,执行install.sh的脚本的时候,会有各种花样的问题,根据报错信息查一下解决方案再解决
- 例如:the following paackages have unmet dependencies(可能是依赖项存在问题)
- 解决:
sudo apt --fix-broken install,然后sudo apt-get autoremove会自动删除一些太旧或者不合适的依赖项(这个功能是我自己的理解)
Mininet拓扑构建与命令使用
1. 打开终端,执行su root切换到root用户
2. 创建拓扑
-
(创建完一种类型后可
exit退出,然后再尝试创建不同类型)-
**创建single拓扑:(单一(Single)**拓扑指整个网络拓扑中交换机有且只有一个,交换机可以下挂一个或多个主机)
sudo mn --topo=single,3:本例创建了一个交换机、3个主机,3个主机都下挂在一个交换机下 -
**创建 linear(线性)拓扑:(线性(linear)**拓扑指交换机连接呈线形排列,且每个交换机所连接主机数目只有一个)
sudo mn --topo=linear,3:本例创建了3个交换机、3个主机,3个主机分别下挂在一个交换机下
-
-
**创建树形(tree)拓扑:(树形(tree)**拓扑指交换机连接成树形排列,且每个交换机所连接主机一般有多个关联使用参数depth及fanout)
sudo mn --topo=tree,depth=2,fanout=2:本例创建了depth为2,fanout为2的拓扑,表示交换机深度即层数为2,每个交换机下挂2个设备 -
创建自定义拓扑:(自定义(custom)拓扑指python编写文件file.py,执行此脚本即可创建定义的拓扑,—custom与—topo联用)
# cd /home/openlab/openlab/mininet/custom# sudo mn --custom topo-2sw-2host.py --topo mytopo: 本例在custom目录下存在topo-2sw-2host.py文件,调用此文件构建拓扑
3. 内部交互命令的使用
- 显示链接信息:
net - 查看节点信息:
nodes - 查看链路健壮性信息:
links - 验证所有主机间通信并查看结果:
pingall - 开启 xterm 进入设备可视化操作界面
- 退出Mininet:
exit - 清除释放Mininet构造配置的交换机及主机:
mn -c - 查看获取帮助:
mn --help或者mn -h
Mininet常用命令总结:
| 命令 | 作用 |
|---|---|
| help | 默认列出所有命令文档,后面加命令名将介绍该命令用法 dump打印节点信息 |
| gterm | 给定节点上开启gnome-terminal 注:可能导致mn崩溃 |
| xterm | 给定节点上开启xterm |
| intfs | 列出所有的网络接口 |
| iperf | 两个节点之间进行简单的iPerf TCP测试 |
| iperfudp | 两个节点之间用制定带宽UDP进行测试 |
| net | 显示网络链接情况 |
| noecho | 运行交互式窗口,关闭回应(echoing) |
| pingpair | 在前两个主机之间互Ping测试 |
| source | 从外部文件中读入命令 |
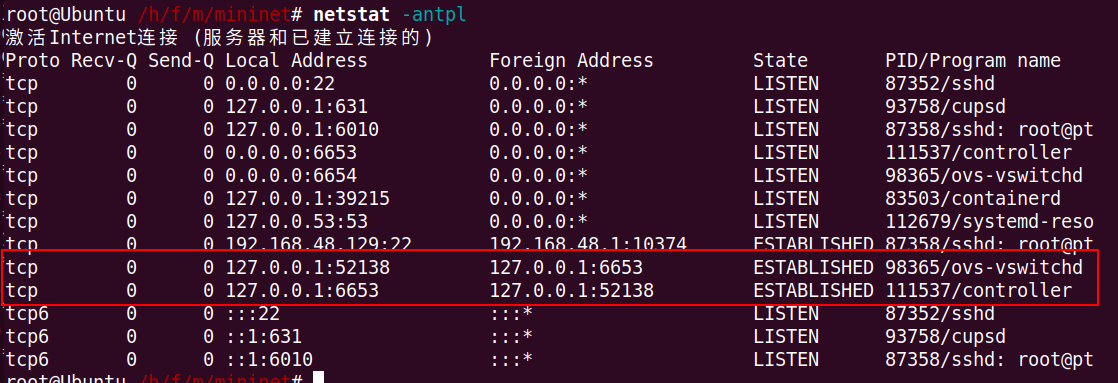
| dpctl | 在所有交换机上用dptcl执行相关命令,本地为tcp 127.0.0.1:6634 |
| link | 禁用或启用两个节点之间的链路 |
| nodes | 列出所有的节点信息 |
| pingall | 所有主机节点之间互Ping |
| py | 执行Python表达式 |
| sh | 运行外部shell命令 |
| quit/exit | 退出 |
4. Mininet 可视化构建网络拓扑
-
启动 MiniEdit
cd /home/openlab/openlab/mininet/examples sudo ./miniedit.py -
Mininet 拓扑建立(选择左侧的网络组件,在空白区域单击鼠标左键即可添加网络组件,可选择的组件主要有主机、OpenFlow交换机、传统交换机,传统路由器、链路、控制器)

- Miniedit 属性配置(进行鼠标右击长按,选择Properties即可进行配置,设备属性配置OK后,将会在miniedit.py执行的后台(终端)产生日志,告知所添加的设备属性)



-
Miniedit 全局配置(Miniedit左上角“Edit”中可以剪切删除设备,及对整个网络进行全局配置)

-
Miniedit 运行(点击左下角“run”,即可运行设置好的网络拓扑,同时在后台可以看到相应的配置信息。运行后对交换机、主机进行右击长按,可查看交换机的bridge信息及打开Host的终端)
-
Miniedit 保存脚本(miniedit设置好拓扑后,可通过选择File-Export Level 2 Script,将其保存为python脚本,默认在mininet/examples目录下,通过chmod给此脚本权限后,直接运行即可重现拓扑。)
-
Miniedit 脚本执行
chmod -R 777 sdnlab.py: 通过后台查看保存的sdnlab.py脚本文件,并给脚本赋予权限./sdnlab.py: 执行sdnlab.py脚本
Mininet 调用API扩展自定义拓扑
-
cd /home/openlab/openlab/mininet/custom:进入custom目录 -
sudo mn --custom topo-2sw-2host.py --topo mytopo: 在custom目录下创建自定义拓扑 -
py net.addHost(‘h3’): 在Mininet交互环境中添加主机h3 -
py net.addLink(s3,net.get(‘h3’)): 添加s3与主机h3之间的链路 -
py s3.attach(‘s3-eth3’): 添加接口 -
py net.get(‘h3’).cmd(‘ifconfig h3-eth0 10.3’): 对主机进行配置IP地址 -
查看节点信息
dump nodes -
验证主机间的连通性(建议先不用pingall,先使用两个主机间的ping操作)
h1 ping h3 pingall
还没做完笔记,之后再补充