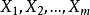文章目录
- 前言
- 边缘概率
- 联合概率
- 定义
- 分析
- 条件概率
- 定义
- 问条件概率能举个例子吗
- 问条件概率在图中表示的是哪一块呢?
- 条件概率习题:
- 全概率
- 定义
- 推导
- 全概率习题
- 贝叶斯公式
- 定义
- 推导
- 贝叶斯定理习题
- 结束语
前言
条件概率,边缘概率,联合概率,全概率,贝叶斯定理是机器学习中几乎所有算法的基础,虽然公式记住了,但是为什么是这样,以及如何理解看过之后隔一段时间问题忘,这里在这里好好做下总结
边缘概率
边缘概率是与联合概率相对应的, P ( A ) P(A) P(A)和 P ( B ) P(B) P(B)这类仅与单个随机变量有关的概率称为边缘概率。
边缘概率是不用求的,一般都会给出。
条件概率是由联合概率反推出来的,理解起来没有那么直观,全概率,贝叶斯定理也是由联合概率推导出来的,所以这里先说联合概率再说条件概率,最后再讲贝叶斯定理。
联合概率
定义
指包含多个条件且所有条件同时成立的概率,记作 P ( A , B ) P(A, B) P(A,B),或 P ( A B ) P(AB) P(AB)或 P ( A ∪ B ) P(A \cup B) P(A∪B),不过一般都是写成 P ( A , B ) P(A, B) P(A,B)。
分析
事件A和事件B可以相互影响的,不过也可以相互独立,不过没有讨论的意义。

如上图
绿色的椭圆表示事件A发生的概率 P ( A ) P(A) P(A)
橘红色的椭圆表示事件B发生的概率 P ( B ) P(B) P(B)
A和B相交的部分就是 P ( A , B ) P(A,B) P(A,B)发生的概率
其中
P ( A ) P(A) P(A)和 P ( B ) P(B) P(B)都是边缘概率
P ( A , B ) P(A,B) P(A,B)就是联合概率
于是我们可以很
可以看到事件A发生的概率和事件B相交的部分就是 P ( A , B ) P(A,B) P(A,B)
然后我们也就很容易理解
P ( A , B ) P(A,B) P(A,B)发生的概率就是:
事件B发生的概率,乘以事件A在事件B发生的条件下发生的概率,
于是有: P ( A , B ) = P ( B ) P ( A ∣ B ) P(A,B) = P(B) P(A|B) P(A,B)=P(B)P(A∣B)
其中 P ( A ∣ B ) P(A| B) P(A∣B)就是事件B发生的情况下事件A发生的概率就是条件概率,记为 P ( A ∣ B ) P(A|B) P(A∣B),下文会继续讲到。
条件概率
定义
已知事件A发生的条件下,另一个事件B发生的概率称为条件概率,即为: P ( A ∣ B ) P(A|B) P(A∣B)
事件A和事件B是相互影响的。更通俗地说事件A与事件B是有关系的,发生事件A会影响发生事件B发生的概率。
问条件概率能举个例子吗
学生时代两个人竞选班,同学A赢的概率是0.6,同学B赢的概率是0.4,问同学A在同学B先被投票的情况下赢的概率是多少。
心理学上有种先入为主的现象,不管是谁,第一个被投票的往往比第二个得票更多一些,就这就是两个事件相互影响,这就是条件概率
问条件概率在图中表示的是哪一块呢?
答:条件概率 P ( A ∣ B ) P(A|B) P(A∣B)在图中表示不出来, P ( A , B ) P(A,B) P(A,B)和 P ( B ) P(B) P(B)都是以图形的形式表示概率的, P ( A ∣ B ) P(A|B) P(A∣B)则是 P ( A ∣ B ) P(A|B) P(A∣B)是 P ( A , B ) P(A,B) P(A,B)除以 P ( B ) P(B) P(B)的比值,在图形上表示不出来。
条件概率毕竟还是有些抽象滴。。。要不然也不会主要求它啊(_)
P ( A ∣ B ) P(A|B) P(A∣B)是通过联合概率反推出来的,以图形化的方式表示自然没有那么直观,不过以联合概率反推的方式来解理还是很好理解的,参考联合概率
OK,到这里来道习题加深下理解吧
条件概率习题:
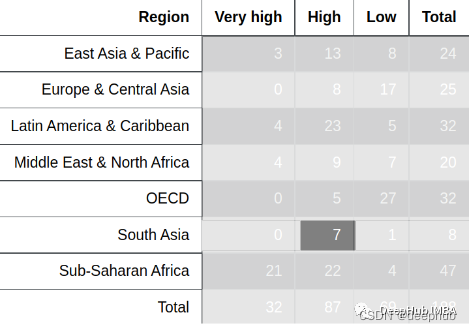
从 1 , 2 , 3 , … , 15 1,2,3,\ldots ,15 1,2,3,…,15中甲乙两人各任取一个数字(不重复),已知甲取到的数是5的倍数,求甲数大于乙数的概率。
解:
设事件A表示”甲取到的数比乙大“,即 P ( A ) P(A) P(A)
设事件B表示”甲取到的数是5的倍数”,即 P ( B ) P(B) P(B)
则显然所要就是条件概率 P ( A ∣ B ) P(A|B) P(A∣B)
根据公式
P ( A ∣ B ) = P ( A , B ) P ( B ) P(A|B) = \frac{P(A,B)}{P(B)} P(A∣B)=P(B)P(A,B)
而:
P ( B ) = 3 15 = 1 5 P(B) = \frac{3}{15} = \frac{1}{5} P(B)=153=51
P ( A , B ) = C 4 1 + C 9 1 + C 14 1 C 14 1 C 15 1 = 9 / 70 P(A,B) = \frac{C^1_4 + C^1_9 + C^1_{14}}{C^1_{14}C^1_{15}} = 9 / 70 P(A,B)=C141C151C41+C91+C141=9/70
则
P ( A ∣ B ) = P ( A , B ) P ( B ) = 9 70 P(A|B) = \frac{P(A,B)}{P(B)} = \frac{9}{70} P(A∣B)=P(B)P(A,B)=709
所以 P ( A ∣ B ) = 9 14 P(A|B) = \frac{9}{14} P(A∣B)=149
通过这么一个例子,理解起来是不是更深入了?
我们可以发现:
- P ( B ) P(B) P(B)是边缘概率,是直接可以求出来的,
- P ( A ) 与 P ( B ) P(A)与P(B) P(A)与P(B)是相互影响的,
- P ( A , B ) P(A,B) P(A,B)是联合概率通过复杂些的计算也是可以求出来的,
但是条件概率P(A|B)则比较抽象,没那么容易求出来,
OK,现在知道了条件概率的意义了吧
全概率
定义
联合概率中把事件A分割成事件 A 1 , A 2 , A 3 , ⋯   , A n A_1,A_2,A_3, \cdots, A_n A1,A2,A3,⋯,An,并把A与B的位置对调于是就成了全概率,如下图

推导
只是全概率是求事件B的,
全概率需要满足以下条件:
- 事件A1到An是相互独立的
- 事件A1到An组成了整个样本空间A
- 事件A1到An能把事件B无重叠地覆盖掉
如上图,事件B发生的概率是由C1~C6组成的,于是有:
P ( B ) = P ( C 1 ) + P ( C 2 ) + P ( C 3 ) + P ( C 4 ) + P ( C 5 ) + P ( C 6 ) P(B) = P(C_{1}) + P(C_{2}) + P(C_{3}) + P(C_{4}) + P(C_{5}) + P(C_{6}) P(B)=P(C1)+P(C2)+P(C3)+P(C4)+P(C5)+P(C6)
简化一下就是: P ( B ) = ∑ i = 1 6 P ( C i ) P(B) = \sum_{i=1}^{6}P(C_{i}) P(B)=i=1∑6P(Ci)
而 P ( C i ) = P ( B ∣ A i ) P(C_{i}) = P(B | A_{i}) P(Ci)=P(B∣Ai)
于是全概率公式就出来了
P ( B ) = ∑ i = 1 n P ( B ∣ A i ) P(B) = \sum_{i=1}^{n}P(B | A_{i}) P(B)=i=1∑nP(B∣Ai)
注意啊,到全概率的时候A( A i A_{i} Ai)与B,的位置就反过来了,比如说
条件概率公式的表示形式是: P ( A ∣ B ) P(A|B) P(A∣B)
全概率公式的表示形式是: P ( B ∣ A i ) P(B|A_{i}) P(B∣Ai)
好了,来道题吧:
全概率习题
某工厂有两个车间产生同一型号的配件,第一车间的次品率是 0.15 0.15 0.15,第二车间的次品率是 0.12 0.12 0.12,两个车间的成品都混合堆放在一直,假设第1,2车间生产的成品比例为 2 : 3 2:3 2:3,现有一客户从混合成品堆里随机抽查一台产品,求该产品的合格率。
解:
设
事件B = {从仓库中随机抽查的产品的合格率}
事件A_{i} = {抽的是第 i i i车间产生的}, i = 1 , 2 i = 1, 2 i=1,2
于是
P ( B ) = ∑ i = 1 2 P ( A i ) P ( B ∣ A i ) P(B) = \sum_{i=1}^{2}P(A_{i})P(B| A_{i}) P(B)=i=1∑2P(Ai)P(B∣Ai)
由题意可知:
A 1 A_1 A1的边缘概率:
P ( A 1 ) = 2 5 P(A_{1}) = \frac{2}{5} P(A1)=52
A 2 A_2 A2的边缘概率:
P ( A 2 ) = 3 5 P(A_{2}) = \frac{3}{5} P(A2)=53
条件概率:
A 1 A_1 A1发生的情况下,B发生的概率:
P ( B ∣ A 1 ) = P ( B , A 1 ) P ( A 1 ) P(B|A_{1}) = \frac{P(B, A_{1})}{P(A_{1})} P(B∣A1)=P(A1)P(B,A1)
P ( B ∣ A 1 ) = 0.85 P(B|A_{1}) = 0.85 P(B∣A1)=0.85
A 2 A_2 A2发生的情况下,B发生的概率:
P ( B ∣ A 2 ) = P ( B , A 2 ) P ( A 2 ) P(B|A_{2}) = \frac{P(B, A_{2})}{P(A_{2})} P(B∣A2)=P(A2)P(B,A2)
P ( B ∣ A 2 ) = 0.88 P(B|A_{2}) = 0.88 P(B∣A2)=0.88
根据全概率公式可知:
P ( B ) = P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) P(B) = P(A_{1})P(B| A_{1}) + P(A_{2})P(B| A_{2}) P(B)=P(A1)P(B∣A1)+P(A2)P(B∣A2)
所以 P ( B ) = 0.868 P(B) = 0.868 P(B)=0.868
贝叶斯公式
定义
同样条件概率中把A推分割成 A 1 , A 2 , A 3 , ⋯   , A n A_1,A_2,A_3, \cdots, A_n A1,A2,A3,⋯,An,并把A与B的位置对调就成了贝叶斯公式
推导

根据上图(没错,两个图是一样的,只是离得太远看着不方便)
我们可以知道:求事件B发生的情况下 A i A_i Ai发生的概率其实就是求: P ( C i ) P(C_i) P(Ci)
而根据条件概率我们可以知道:
P ( C i ) = P ( A i ∣ B ) = P ( B , A i ) P ( B ) P(C_{i}) = P(A_i | B) = \frac{P(B, A_{i})}{P(B)} P(Ci)=P(Ai∣B)=P(B)P(B,Ai)
由全概率公式我们可以知道:
P ( B ) = ∑ j = 1 n P ( A j ) P ( B ∣ A j ) P(B) = \sum_{j=1}^{n}P(A_{j})P(B|A_{j}) P(B)=j=1∑nP(Aj)P(B∣Aj)
于是我们最终得到贝叶斯定理的公式为(注意 i i i与 j j j的不同):
P ( A i ∣ B ) = P ( B , A i ) ∑ j = 1 n P ( A j ) P ( B ∣ A j ) P(A_{i}|B) = \frac{P(B, A_{i})}{\sum_{j=1}^{n}P(A_{j})P(B|A_{j})} P(Ai∣B)=∑j=1nP(Aj)P(B∣Aj)P(B,Ai)
同样来道习题
贝叶斯定理习题
某公路上经过的货车与客车的数量之比为 2 : 1 2:1 2:1,货车中途停车修理的概率为 0.02 0.02 0.02,客车为 0.01 0.01 0.01,现有一辆汽车中途停车修理,问该汽车是货车的概率
解:
设
事件 B B B = {中途停车修理}
事件 A 1 A_1 A1 ={经过的是货车},
事件 A 2 A_2 A2 ={经过的是客车},
于是事件B有: B = A 1 B ∪ A 2 B B = A_{1}B \cup A_{2}B B=A1B∪A2B
由贝叶斯公式有:
P ( A 1 ∣ B ) = P ( A 1 ) P ( B ∣ A 1 ) P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) P(A_{1} | B) = \frac{P(A_1)P(B|A1)}{P(A_1)P(B|A1) + P(A_2)P(B|A_2)} P(A1∣B)=P(A1)P(B∣A1)+P(A2)P(B∣A2)P(A1)P(B∣A1)
P ( A 1 ∣ B ) = 2 3 × 0.02 2 3 × 0.02 + 1 3 × 0.01 P(A_{1} | B) = \frac{\frac{2}{3} × 0.02}{\frac{2}{3} × 0.02 + \frac{1}{3} × 0.01} P(A1∣B)=32×0.02+31×0.0132×0.02
所以最后的结果为: P ( A 1 ∣ B ) = 0.80 P(A_{1} | B) =0.80 P(A1∣B)=0.80
结束语
OK,到这里边缘概率,联合概率,条件概率,全概率,贝叶斯定理就全部完了,不知道你有没有看明白,不明白的话可以提问啊,咱一块交流。




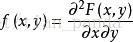

![概率统计篇:概率基础(联合概率、条件概率和贝叶斯法则)[第二天]](https://img-blog.csdnimg.cn/2019103110320458.png)