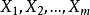在隐马尔可夫(HMM)和条件随机场(CRF)中有很多概率计算问题,要想理解他们,必须先把概率的一些概念及计算公式搞清楚。本文旨在用形象的图形和具体事例来讲解这些概念和公式,以帮助理解。这里讲的部分内容可以在5分钟理解贝叶斯公式一文中有提到。
边缘概率:一个随机事件X的发生概率,记做P(X),比如今天下雨这个事件的概率,而这件事不发生的概率是1-P(X),也就是今天不下雨的概率,有时会记做: $$ P(\overline{X}) $$
联合概率:在X事件和Y事件都同时发生的概率,记做P(Y,X),比如今天下雨是X事件,我出门是Y事件。我下雨有时会出门,有时不出门,而我P(X,Y)表示在一段时间里(比如一年),我在下雨天出门概率 或频率(计算时概率经常用频率来统计),即:$$\frac{下雨天时我出门的天数}{365}$$
条件概率:在X事件和Y事件同时发生的频率与X事件发生频率的比值。如果用字面意思来理解条件概率,那条件概率的概念很容易和联合概率搞混。字面意思是在X事件发生的条件下Y发生的概率,这无法与X事件发生同时Y也发生的概率区分。所以一定要理解为一个比值,才不至于搞混。X发生时Y的条件概率记做P(Y|X),计算时是X和Y的联合概率与X发生概率的比值。比如一年中下雨天有200天,在这200天的下雨天中我有20天出门,在不下雨的165天中我出门了100天,我在下雨天出门的条件概率为:
$$P(Y|X)=\frac{P(X,Y)}{P(X)} = \frac{20/365}{200/365} = 0.1$$
条件概率中的X和Y其实没有必然的条件-结果关系,X和Y是可以颠倒过来的,所以按字面意思理解X条件导致Y发生的概率就会理解不了数学上的P(X|Y),但是理解为比值就没问题。我出门时老天下雨的条件概率为:
$$P(X|Y)=\frac{P(X,Y)}{P(Y)} = \frac{20/365}{(20+100)/365} = \frac{20}{(20+100) = 0.167} $$
因为我有120天(其中雨天出门20天,不下雨出门100天)是出门的,所以P(Y)=120/365
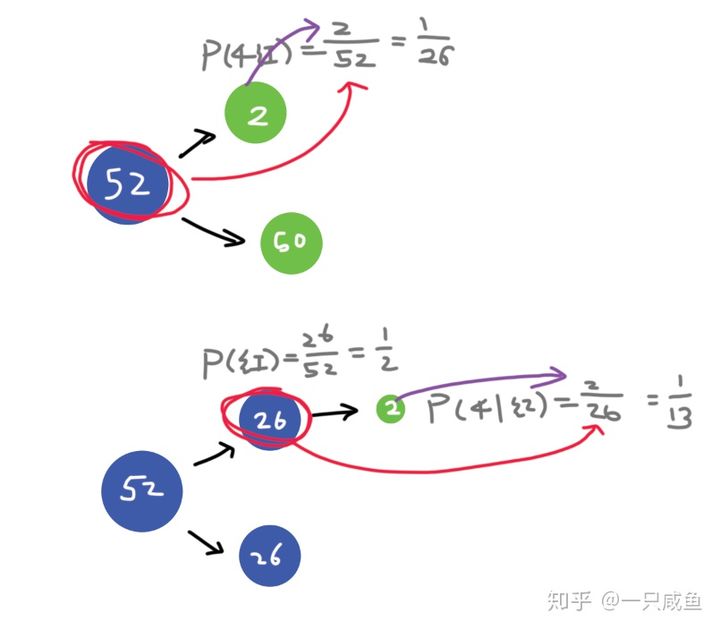
下面用个图来表示,更加形象些:

当方框总面积为1时,每个圆的面积就代表了边缘概率P(X)或P(Y),交叉部分就代表了X和Y同时发生的联合概率P(X,Y)
而交叉部分的面积与P(X)面积之比为P(Y|X),与P(Y)的面积之比为P(X|Y)
P(X|Y)与P(X,Y)的大小怎么比较呢?其实把P(X,Y)当成交叉部分面积与方框面积(面积为1)之比就可以比较两个占比了。
随机事件独立:事件X和事件Y相互独立,按字面意思可以理解为,X的发生与否,对Y的发生概率没有影响,反之,Y发生与否对X发生的概率没有影响。举个例子,如果今天股市的上涨是X,今天下雨是Y。很明显今天在某个城市是否下雨,对股市是涨是跌不会有任何影响。这是从生活常识中理解的。但是数学是讲究数据证据的,我们需要根据过去发生的历史数据统计来判断两者是独立还是有关联。那数学上怎么判断两者独立或关联的呢?如果条件概率P(Y|X)=P(Y),则表示X与Y独立。


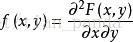

![概率统计篇:概率基础(联合概率、条件概率和贝叶斯法则)[第二天]](https://img-blog.csdnimg.cn/2019103110320458.png)