【例题】
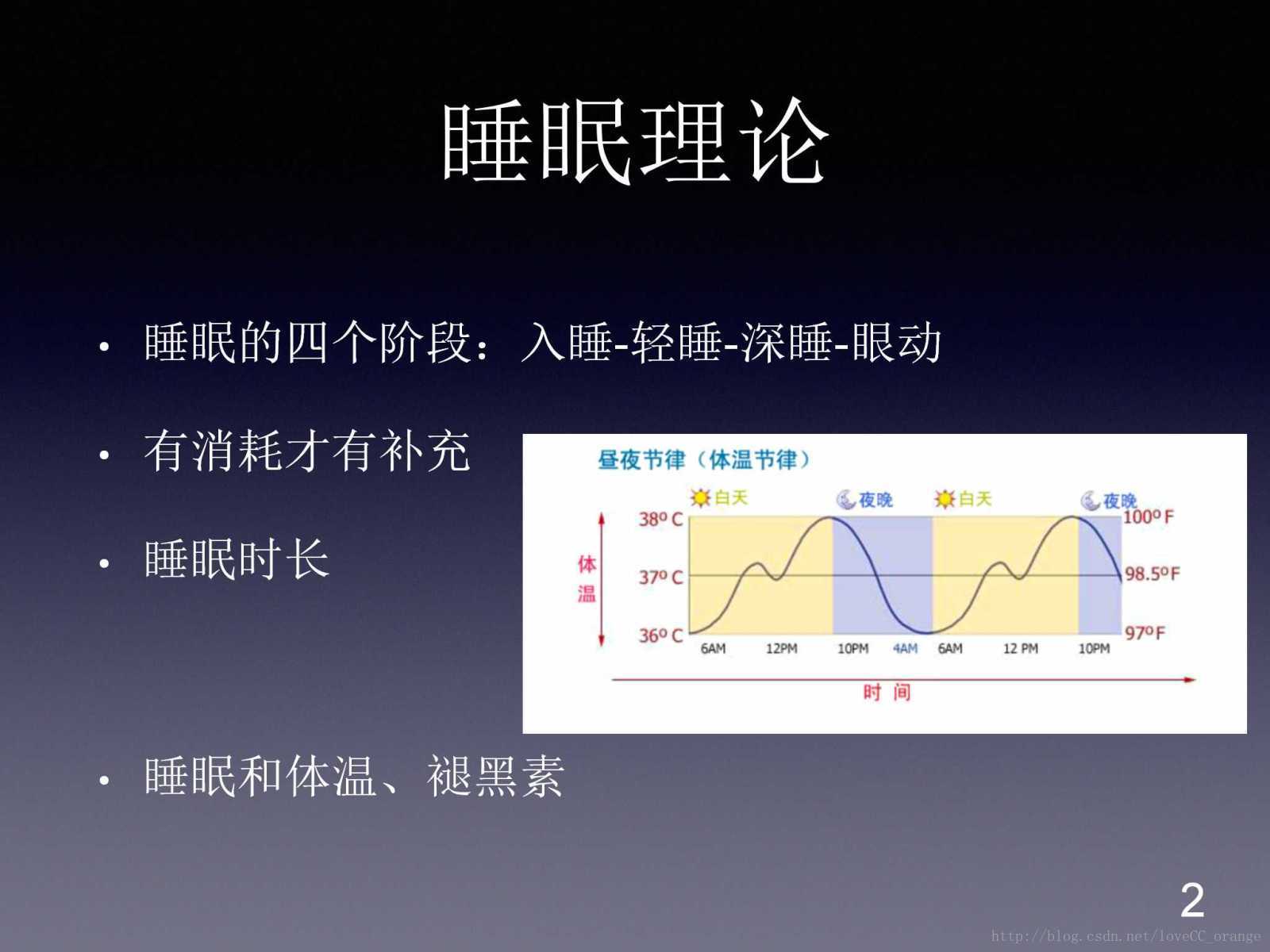
设X和Y的联合密度函数为:
f ( x , y ) = { 2 0 < x < ∞ , 0 < y < ∞ 0 其 他 区 域 f(x,y)=\left\{ \begin{array}{rcl} 2 && {0<x<\infty,0<y<\infty}\\ 0 && 其他区域 \end{array} \right. f(x,y)={200<x<∞,0<y<∞其他区域
计算(1)P{X>1,Y<1} (2)P{X<Y}
类型题概述
这类给联合密度函数求概率的题实质上就是二重积分,被积函数是联合密度函数,积分区域是两个给出区域的交集:联合密度函数有意义的区域(即不为零的区域)与所求概率花括号中表示的区域(没看懂?没关系,结合例题秒懂!)
例题解析
来看具体例题:
(1) P{x>1, Y<1}
首先联合密度函数不为零的区域是:(为零的区域没有意义不考虑)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-41bXHbrC-1590228919520)(C:\Users\Lenovo\AppData\Roaming\Typora\typora-user-images\image-20200523175806901.png)]](https://img-blog.csdnimg.cn/20200523181604519.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDU1OTc1Mg==,size_16,color_FFFFFF,t_70)
然后第(1)题的所求概率区域是:x>1, Y<1(P{x>1, Y<1}) 即最后的积分区域D是两区域的交集——图中黄色部分
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dyesg0Kz-1590228919527)(C:\Users\Lenovo\AppData\Roaming\Typora\typora-user-images\image-20200523175713599.png)]](https://img-blog.csdnimg.cn/20200523181641276.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDU1OTc1Mg==,size_16,color_FFFFFF,t_70)
对图中黄色区域D求联合密度的二重积分就可以了。(再次:联合密度为0的部分不考虑)
(1) P{x>1, Y<1}
= ∬ 2 e − x e − 2 y d x d y =\displaystyle\iint2e^{-x}e^{-2y}dxdy =∬2e−xe−2ydxdy
= ∫ 1 + ∞ d x ∫ 0 1 2 e − x e − 2 y d y =\displaystyle\int_1^{+\infty}dx\int_0^12e^{-x}e^{-2y}dy =∫1+∞dx∫012e−xe−2ydy
= ( 1 − e − 2 ) ∫ 1 + ∞ e − x d x =(1-e^{-2})\displaystyle\int_1^{+\infty}e^{-x}dx =(1−e−2)∫1+∞e−xdx
= e − 1 − e − 3 =e^{-1} - e^{-3} =e−1−e−3
(计算可能存在错误。你看看方法就行)
同理,(2)的联合密度函数没有变,所以它的被积函数与有效区域(紫色)也没有变。但求的概率不一样(P{x<y})所以二者交叠的黄色区域如图所示:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-faapjIDY-1590228919530)(C:\Users\Lenovo\AppData\Roaming\Typora\typora-user-images\image-20200523180817189.png)]](https://img-blog.csdnimg.cn/20200523181658717.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDU1OTc1Mg==,size_16,color_FFFFFF,t_70)
P{x<y}
= ∬ 2 e − x e − 2 y d x d y =\displaystyle\iint2e^{-x}e^{-2y}dxdy =∬2e−xe−2ydxdy
= ∫ 0 + ∞ d x ∫ 0 x 2 e − x e − 2 y d y =\displaystyle\int_0^{+\infty}dx\int_0^x2e^{-x}e^{-2y}dy =∫0+∞dx∫0x2e−xe−2ydy
= ∫ 1 + ∞ e − x − e − 3 x d x =\displaystyle\int_1^{+\infty}e^{-x}-e^{-3x}dx =∫1+∞e−x−e−3xdx
= e − 1 − e − 3 =e^{-1} - e^{-3} =e−1−e−3
小结
再来看这句话:这类给联合密度函数求概率的题实质上就是二重积分,被积函数是联合密度函数,积分区域是两个给出区域的交集:联合密度函数有意义的区域(即不为零的区域)与所求概率花括号中表示的区域
是不是很easy!恭喜你学会了!
(啊今天居然有人问我概率论的题那我随便写一下吧。啊既然写了不如水一篇博客叭。顺带一提这里计算结果不一定是正确的因为博主我实在是口算笔算二重渣) 不重要大家掌握方法就好啦。希望对你有帮助!做错了请一定要告诉俺一声。。溜了溜了。。。







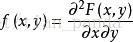

![概率统计篇:概率基础(联合概率、条件概率和贝叶斯法则)[第二天]](https://img-blog.csdnimg.cn/2019103110320458.png)