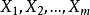mininet介绍
一、Mininet是什么
Mininet是由斯坦福大学基于Linux Container架构开发的一个进程虚拟化网络仿真工具,可以创建一个包含主机,交换机,控制器和链路的虚拟网络,其交换机支持OpenFlow,具备高度灵活的自定义软件定义网络。
二、Mininet可以做什么
为OpenFlow应用程序提供一个简单,便宜的网络测试平台;
启用复杂的拓扑测试,无需连接物理网络;
具备拓扑感知和OpenFlow感知的CLI,用于调试或运行网络范围的测试;
支持任意自定义拓扑,主机数可达4096,并包括一组基本的参数化拓扑;
提供用户网络创建和实验的可拓展Python API。
三、Mininet的优势
Mininet结合了许多仿真器,硬件测试床和模拟器的有优点:
与仿真器比较:启动速度快;拓展性大;带宽提供多;方便安装,易使用。
与模拟器比较:可运行真实的代码;容易连接真实的网络。
与硬件测试床比较:便宜;快速重新配置及重新启动。
四、Mininet的主要特性
Mininet作为一个轻量级软定义网络研发和测试平台,其主要特性包括:
支持OpenFlow、Open vSwitch等软定义网络部件;
方便多人协同开发;
支持系统级的还原测试;
支持复杂拓扑、自定义拓扑;
提供python API;
很好的硬件移植性(Linux兼容),结果有更好的说服力;
高扩展性,支持超过4096台主机的网络结构。
mininet安装
环境:Ubuntu18.04 (其他Linux操作系统也可)
下载源码:
git clone git://github.com/mininet/mininet
然后进入mininet/util目录,执行安装命令-a表示全部安装
cd mininet
cd util
sudo ./install.sh -a
其他安装方式
mininet/util/install.sh -a 在home目录下安装Mininet所需的所有的东西,包括Open vSwitch、wireshark和POX控制器等
mininet/util/install.sh -s mydir -a 在指定的目录下安装Mininet所需的所有的东西
mininet/util/install.sh -nfv 在home目录下安装Mininet、OpenFlow推荐的交换机和Open vSwitch
mininet/util/install.sh -s mydir -nfv 在指定的目录下安装Mininet、OpenFlow推荐的交换机和Open vSwitch
在home目录下安装Mininet所需的所有的东西,包括Open vSwitch、wireshark和POX控制器等
全部安装的话需要的时间稍微比较长,稍安勿躁
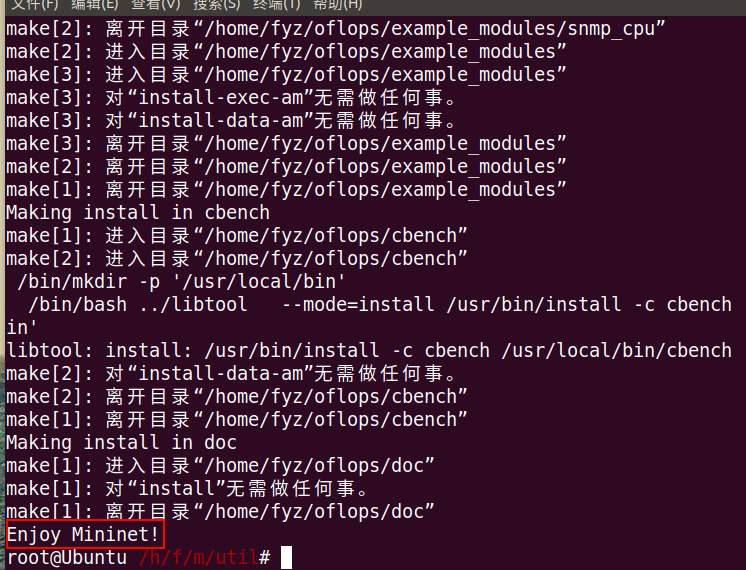
看到Enjoy Mininet就是已经安装成功了
启动mininet
mn
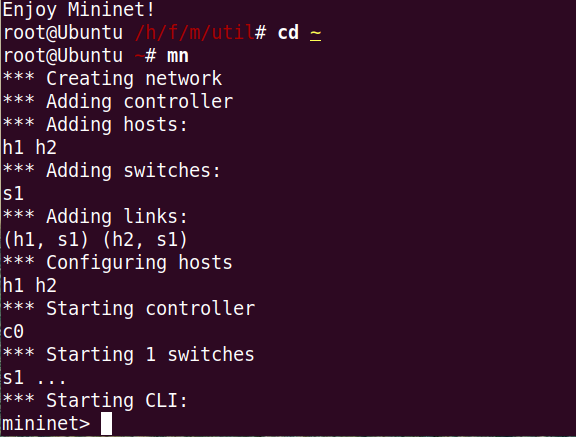
这里介绍一下
h 代表 host 即主机
s 代表 switch 即交换机 (这里的交换机不是普通的交换机,是openvswitch 是一种支持SDN(OpenFlow 协议)的交换机)
c 代表 controller 即 控制器(SDN控制器)
什么是Open vSwitch
OpenvSwitch简称OVS,正如其官网(http://openvswitch.org/)所述,OVS是一个高质量、多层的虚拟交换软件。它的目的是通过编程扩展支持大规模网络自动化,同时还支持标准的管理接口和协议。
随着虚拟化应用普及,需要部署更多的虚拟化交换机,而费用昂贵的闭源虚拟交换机让用户不堪重负,多层虚拟化软件交换机Open vSwitch由Nicira Networks开发,主要实现代码为可移植的C代码。它遵循Apache 2.0开源代码版权协议,可用于生产环境,支持跨物理服务器分布式管理、扩展编程、大规模网络自动化和标准化接口,实现了和大多数商业闭源交换机功能类似的软件交换机。
OVS官方的定位是要做一个产品级质量的多层虚拟交换机,通过支持可编程扩展来实现大规模的网络自动化。设计目标是方便管理和配置虚拟机网络,检测多物理主机在动态虚拟环境中的流量情况。针对这一目标,OVS具备很强的灵活性。可以在管理程序中作为软件switch运行,也可以直接部署到硬件设备上作为控制层。
详细可以看这篇文章: https://blog.csdn.net/qq_15437629/article/details/74858832
SDN控制器
SDN控制器是软件定义网络(SDN)中的应用程序,负责流量控制以确保智能网络。SDN控制器是基于如OpenFlow等协议的,允许服务器告诉交换机向哪里发送数据包。
SDN控制器的种类 :https://blog.csdn.net/qq_29229567/article/details/88313976
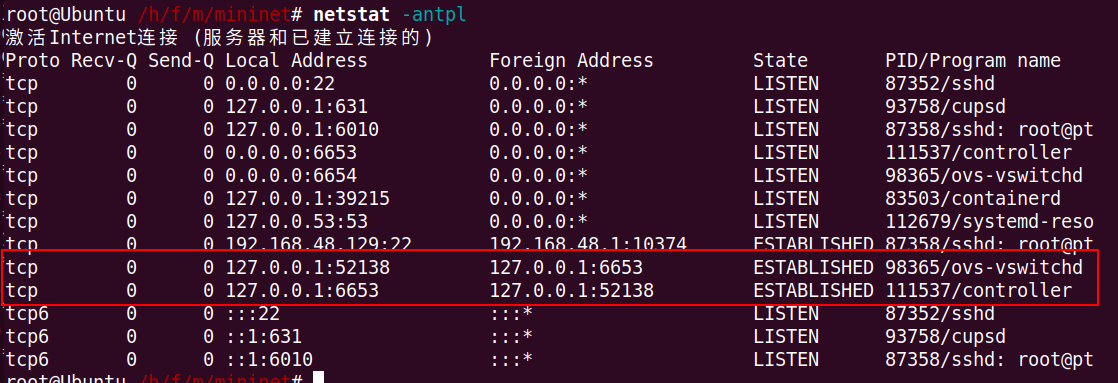
SDN控制器的监听端口是6653 ,openvswitch作为客户端去连接控制器(此时的sdn控制器是pox控制器)
mininet基础操作
mn 启动mininet 默认创建两台主机一个交换机和启动控制器
启动参数总结
-h, --help 打印帮助信息
--switch=SWITCH 交换机类型,包括 [kernel user ovsk]
--host=HOST 模拟主机类型,包括 [process]
--controller=CONTROLLER 控制器类型,包括 [nox_dump none ref remote nox_pysw]
--topo=TOPO,arg1,arg2,...argN 指定自带拓扑,包括 [tree reversed single linear minimal]
-c, --clean清理环境
--custom=CUSTOM 使用自定义拓扑和节点参数
--test=TEST 测试命令,包括 [cli build pingall pingpair iperf all iperfudp none]
-x, --xterms 在每个节点上打开 xterm
--mac 让MAC 地址跟 DP ID 相同
--arp 配置所有 ARP 项
-v VERBOSITY, --verbosity=VERBOSITY [info warning critical error debug output] 输出日志级别
--ip=IP 远端控制器的IP地址
--port=PORT 远端控制器监听端口
--innamespace 在独立的名字空间内
--listenport=LISTENPORT 被动监听的起始端口
--nolistenport 不使用被动监听端口
--pre=PRE 测试前运行的 CLI 脚本
--post=POST 测试后运行的 CLI 脚本
常用命令总结
help 默认列出所有命令文档,后面加命令名将介绍该命令用法
dump 打印节点信息
gterm 给定节点上开启 gnome-terminal。注:可能导致 Mininet 崩溃
xterm 给定节点上开启 xterm
intfs 列出所有的网络接口
iperf 两个节点之间进行简单的 iperf TCP测试
iperfudp 两个节点之间用指定带宽 udp 进行测试
net 显示网络链接情况
noecho 运行交互式窗口,关闭回应(echoing)
pingpair 在前两个主机之间互 ping 测试
source 从外部文件中读入命令
dpctl 在所有交换机上用 dptcl 执行相关命令,本地为 tcp 127.0.0.1:6634
link 禁用或启用两个节点之间的链路
nodes 列出所有的节点信息
pingall 所有 host 节点之间互 ping
py 执行 Python 表达式
sh 运行外部 shell 命令
quit/exit 退出
sh 运行外部 shell 命令
quit/exit 退出
详细操作参考文章 :
https://blog.csdn.net/qq_29229567/article/details/105230800








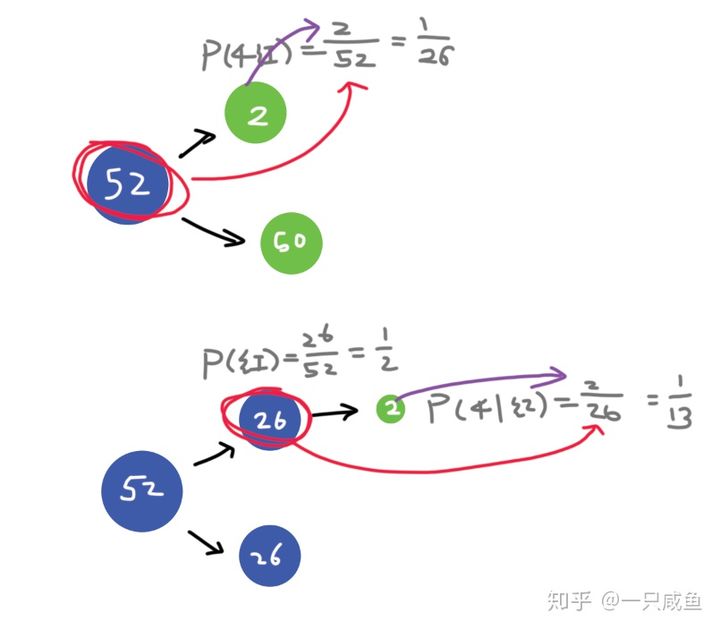


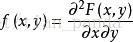

![概率统计篇:概率基础(联合概率、条件概率和贝叶斯法则)[第二天]](https://img-blog.csdnimg.cn/2019103110320458.png)