【写在前面的话】众所周知,线性代数在计算机应用方面也是比较广的(比如人工智能等前沿科技领域)。所以...在CSDN记录线性代数的知识不为过吧,哈哈(//狗头保命)。从这里开始我将详细记录线性代数知识点。想要学线性代数的小伙伴可以跟随我的脚步一起学习一下。(坚持每天至少发一篇)话不多说,我们直接开始。

目录
1.1矩阵及其运算
一,矩阵的概念
二,矩阵的线性运算
三,矩阵的乘法
四,矩阵的转置
一,矩阵的概念
我们先来看一下书上关于 矩阵的标准定义:由m×n个数排成的m行n列数表

称为一个m行n列矩阵,简称为m×n矩阵,其中表示第i行第j列处的元(或称元素),i称为
的行指标,j称为 的列指标。
元是实数的矩阵称为实矩阵,元为复数的矩阵称为复矩阵。一般未加特殊说明,都默认为是实矩阵。
举个简单的例子:如果你看到了一个形如这样的东西
,那么我们可以称它是一个3×5的矩阵,其中“3”表示这个矩阵的行,“4”表示这个矩阵的列(基于此,我们可以利用下标表示矩阵里的任何一个元,如:
=3,
,
=6)。
以为矩阵的概念到此就介绍了吗?(哈哈,同学,你还是太单纯)请接收由矩阵的基础定义而拓展的一系列其他矩阵相关概念的“轰炸”。但是看的时候也不要有太多的心里负担,因为这些概念可以更好的帮助我们理解矩阵。(新增拓展矩阵概念已用“绿色”标记)
系数矩阵:
n元线性方程组

的系数可以组成一个m行n列矩阵

称为方程组的系数矩阵;
增广矩阵:
而系数及常数项可以组成一个m行n+1列矩阵

称为方程组的增广矩阵。
零矩阵:
元全为零的矩阵称为零矩阵,记作或
(注意:m和n之间应该有个“×”,实在打不出来,呜呜呜┭┮﹏┭┮,之后类似的试子也是如此,比如下方的
,
,此后不再复述).如
,
.
当m=n时,称A为n阶矩阵(或n阶方程)。
行矩阵和列矩阵:
只有1行(1×n)或1列(m×1)的矩阵
,
分别称为行矩阵和列矩阵。
对角矩阵:
若矩阵的元=0(i≠j),则称A为对角矩阵,
(i=1,2...,n)称为A的对角元,记作A=diag(
)
例如,
为二阶对角矩阵.
单位矩阵:
对角元全为1的对角矩阵称为单位矩阵,n阶单位矩阵记为,在不致混淆时也记为
,即
要记住
的含义呦~之后会经常用到的
上三角矩阵和下三角矩阵:
形如
的矩阵被称为上三角矩阵和下三角矩阵。
二,矩阵的线性运算
为了讨论矩阵的运算,我们首先给出矩阵相等的概念。
如果A和B都是m×n矩阵,就称A和B为同型矩阵。
两个矩阵A=()和B=(
)如果是同型矩阵,且对应元相等,即
,就称A和B相等。
现在我们介绍矩阵的加法
定义2(矩阵的加法)设矩阵
是两个m×n矩阵,将它们的对应元相加,得到一个新的m×n矩阵
则称矩阵C是矩阵A和B的和,记为C=A+B.
举个栗子🌰:若
那么
值得注意的是,只有同型矩阵才能相加,且同型矩阵之和仍为同型矩阵。
下面介绍矩阵与数的乘积
定义3(矩阵的乘数)设m×n是一个m×n矩阵,k是一个数,则称矩阵
为矩阵A和数k的乘积(简称矩阵的数乘),记为kA.
也就是说,用数k乘矩阵A就是将A中每一元都乘k.
矩阵的加法与数乘统称为矩阵的线性运算。
基于此,容易得出矩阵的线性运算满足下列八条性质。
设A,B,C为同型矩阵,k,l为数.
A+B=B+A
(A+B)+C=A+(B+C)
A+O=A
A+(-A)=O
1A=A
k(lA)=(kl)A
k(A+B)=kA+kB
(k+l)A=kA+lA
三,矩阵的乘法
定义4 设m×p矩阵m×p,p×n矩阵B=
p×n,则由元
构成的m×n矩阵m×n称为矩阵A和B的乘积,记为C=AB.
举个例子:设
则
有定义可知:
(1)A的列数必须等于B的行数,A与B才能相乘;
(2)乘积C的行数等于A的行数,C的列数等于B的列数;
(3) 乘积C中第i行第j列元
等于A的第i行元与B的第j列元对应乘积之和,即

矩阵乘法满足下列运算规律:
结合律 (AB)C=A(BC);
数乘结合律 k(AB)=(kA)B=A(kB),k为数;
分配律 A(B+C)=AB+AC,(B+C)A=BA+CA.
请看下面的例子:设求AB和BA.
显然
在上述例子中我们可以看出矩阵的乘法一般不满足交换律,即一般AB≠BA。
当AB≠BA时,称A与B不可交换;当AB=BA时,称A与B可交换。
由例子还可见,A,B都是非零矩阵,但AB=O.由此可知,矩阵的乘法不满足消去律,即A≠0时,由AB=AC不能推出B=C.
矩阵乘法一般不满足交换律,但是,容易得到如下常用结果:
m×n=
m×n,
×n
=
m×n. 我们称
(k≠0)
为数量矩阵。
n阶数量矩阵与任意n阶矩阵A也是可交换的,这是因为
我们还可定义方阵的幂和方阵的多项式.
定义 5 设A是n阶方阵,k为正整数,定义
由定义可证明:当m,k为正整数时,
但需注意,一般
≠
.
当AB=BA时,
但其逆不真。
定义 6 设f(x)=是x的k次多项式,A是n阶方阵,则
f(A)=
称为方阵A的k次多项式.
由定义容易证明:若f(x),g(x)为多项式,A,B均为n阶方阵,则
f(A)g(A)=f(B)g(B).
但是一般情况下
f(A)g(B)≠g(B)f(A)
这里要注意,一般来说
等等 。但是,由于
(当
时)因而
四,矩阵的转置
把一个矩阵A的行列互换,所得到的矩阵称为A的转置,记为.确切的定义如下
定义 7 设
则称
为A的转置。
显然,m×n矩阵的转置是n×m矩阵.
矩阵的转置满足以下规律:
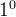
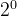
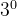
k为数
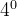
定义 8 若 则称A为对称矩阵;若
,则称A为反称矩阵.
不积跬步无以至千里,不积小流无以成江海
如果对你有帮助的话,点个赞再走呗!