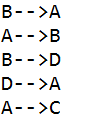1. 相关的概念如下：

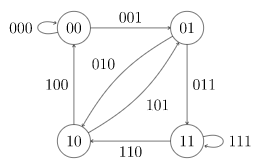
① 有向图G为欧拉回路：当且仅当G的基图连通，且所有顶点的入度等于出度

② 有向图G为欧拉路：当且仅当G的基图连通，而且只存在一个顶点u的入度比出度大于1，只存在一个顶点v的出度比入度大于1（即最多有两个点的入度不等于初度），而且只能从初度比入度大于1的顶点作为起点或者入度比出度大于1的顶点起点这样才可以把图中的所有路径走完

③ 如果一个无向图是连通的，而且最多存在着两个奇点（度数为奇数）那么一定存在欧拉道路，如果有两个奇点那么它们必须是起点和终点，如果奇点不存在，可以从任意的点出发，最终一定会回到该点，成为欧拉回路

所以对于欧拉道路来说选择奇点作为出发点那么肯定能够一次性走完图中的所有边

 

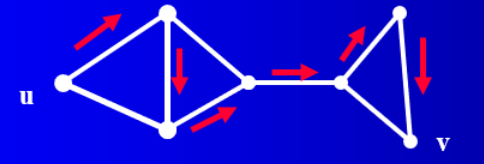
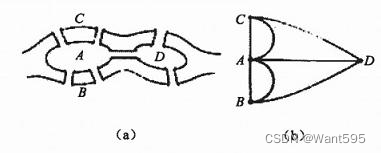
2. 欧拉道路与欧拉回路经常会应用到判断有向图或者无向图的连通性问题，而欧拉道路特别是应用在检验以一个顶点作为起点是否能够以一次性走完图中的所有路径（一笔画）

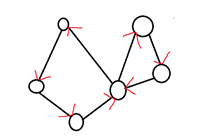
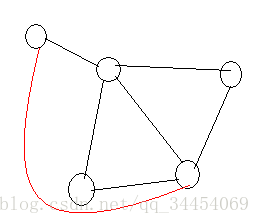
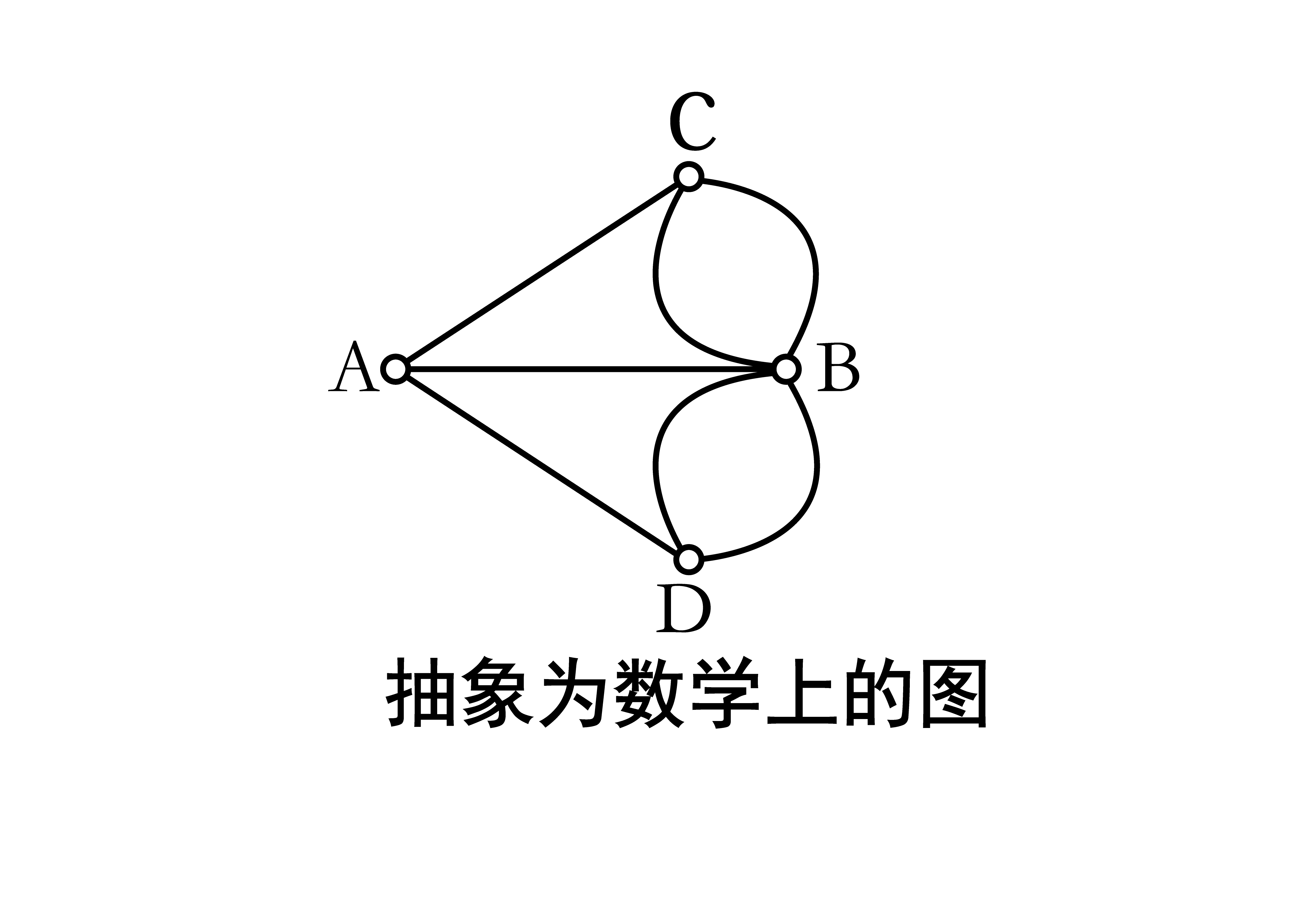
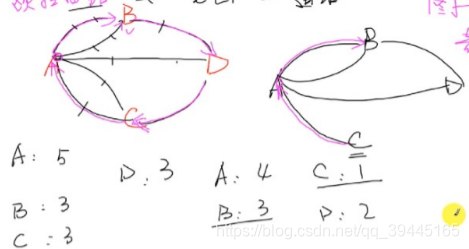
下面是一个欧拉道路的无向图的例子，控制台输入的是一个欧拉道路的无向图（存在两个奇点：顶点的边数为奇数）那么要求输出这个走完欧拉道路的一种可能

思路分析：

① 因为是无向图，所以首先要找到无向图的奇点的边数，因为只有以奇数边的顶点作为起点才能够一次性走完欧拉道路，所以在输入无向图的时候使用一个数组来记录其中顶点的边数，这样输入数据完了之后那么接下来可以使用循环找出奇数边的顶点，顶点可以使用数组的下标来进行代替，例顶点A可以使用下标0代替

② 找到奇数边之后以奇数边的顶点作为起点，深度优先搜索整个无向图直到走完图的所有路径，在找的过程中需要对已经访问过的边进行标记，这里标记边是否被访问过可以使用一个与图相同长度的二维数组，假如我们发现u---->v之间有边而且这条边是没有被访问过的，那么我们需要将对应的访问标记visit[u][v]++，而且visit[v][u]++，因为这个是无向图所以要这样进行标记，而且我们只能走这条边一次，所以这也是标记边是否被刚问过的方法：使用二维数组来进行标记

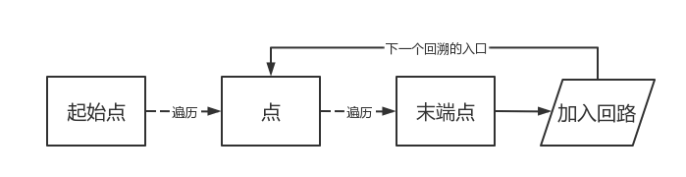
③ 当递归碰到出口的时候说明所有的路径已经走完了，那么它会层层返回，这样我们就可以使用栈这个数据结构来将层层返回的结果压入到堆栈中，因为层层返回它是有最后一层碰到递归出口来进行返回的，所以最后一层的数据表示的是走完欧拉道路的最后的那条边，层层返回之后最开始的也是最开始的出发的地方，所以需要借助栈这个先进后出的特点来存储其中的路径

3. 代码如下：

import java.util.Scanner;
import java.util.Stack;
public class Main {static int graph[][];static int visit[][];static Stack<String> stack = new Stack<String>();public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int edges[] = new int[n];graph = new int[n][n];visit = new int[n][n];for(int i = 0; i < n; i++){int sum = 0;for(int j = 0; j < n; j++){graph[i][j] = sc.nextInt();sum += graph[i][j];}edges[i] = sum;}int x1 = 0, x2 = 0;for(int i = 0; i < n; i++){if(edges[i] % 2 != 0){if(x1 != 0){x2 = i;}else{x1 = i; }if(x1 != 0 && x2 != 0) break;}}//System.out.println(x1 + " " + x2);dfs(x1, n);while(!stack.isEmpty()){System.out.println(stack.pop());}sc.close();}private static void dfs(int u, int n) {for(int v = 0; v < n; v++){if(graph[u][v] > 0 && visit[u][v] < graph[u][v]){//上面使用二维数组是为了更好地标记边是否被访问过visit[u][v]++;visit[v][u]++;dfs(v, n);//不回溯是为了只找出一条路径就可以了直接加入栈中就可以了//当成功走完所有的路径之后会退到到这里然后进行层层返回所以要使用栈这个数据结构stack.add((char)(u + 'A') + "-->" + (char)(v + 'A'));}}}
}