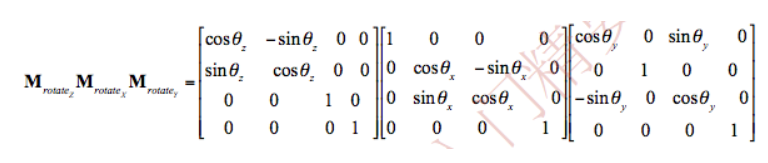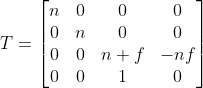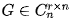矩阵运算法则

（1）矩阵和标量的乘法

（2）矩阵和矩阵的乘法

矩阵相乘的条件 和 结果的行数和列数

变换的基本概念

(1)变换

我们把一些数据，如点、方向矢量甚至颜色等，通过某种方式进行转换的过程

(2)线性变换

线性变换指的是那些可以保留矢量加和标量乘的变换。例如：缩放、旋转、错切、镜像、正交投影等；

(3)平移变换

平移变换不是线性变换，它满足标量乘法，但不满足矢量加法。

(4)仿射变换

合并线性变换和平移变换的变换类型。3D的仿射变换可以使用一个4×4的矩阵来表示，即齐次坐标空间。

（5）齐次坐标

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示；对于一个点，从三维坐标转换成齐次坐标是把其w分量设为1，而对于方向矢量来说，需要把其w分量设为0。

2D 矩阵变换

（1）绕坐标中心旋转 a 角度的变换矩阵

（2）沿坐标轴缩放的变换矩阵

(3) 沿任意N轴缩放的变换矩阵

3D 矩阵变换

（1）绕X轴旋转的变换矩阵

（2）绕Y轴旋转的变换矩阵

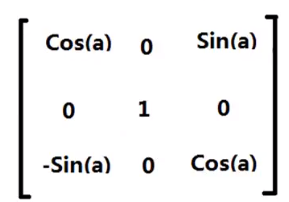
（3）绕Z轴旋转的变换矩阵

（4）3D缩放矩阵

平移矩阵

（1）2D平移矩阵

（2）3D平移矩阵

（3）在3D中绕Y轴先旋转，再平移

变换组合

（1）如何把物体从模型坐标变换到摄像机的投影坐标

第一步：把物体从模型坐标变换到世界坐标：使用物体在模型坐标空间中的顶点 X 模型坐标到世界坐标的矩阵，结果是物体在世界坐标空间中的顶点信息

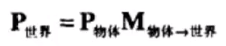
第二步：把物体从世界坐标变化到摄像机的投影坐标：使用物体在时间空间中的顶点信息 X 世界坐标到投影坐标的变换矩阵，结果便是 物体在投影坐标空间中的顶点信息

当然，也可以不用这么麻烦，如果知道模型坐标空间到投影坐标空间的变换矩阵，可以直接使用物体在模型空间中的顶点信息 X 变换矩阵

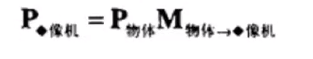
透视投影（小孔成像）

透视投影矩阵

d是摄像机到投影平面的距离

上面的矩阵都是使用 mul(V,M),下面的是 mul(M^T,V),

应用 mul(M^T，V）

（1）把 点（x,y,z）平移 （t_x,t_y,t_z）个单位

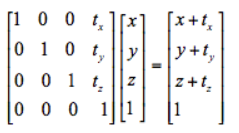
（2）旋转

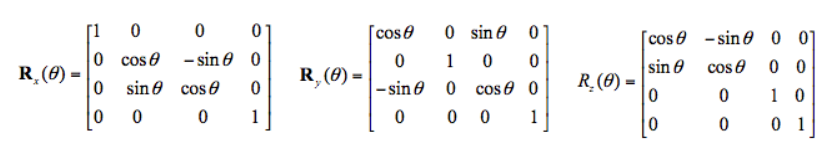
（3）复合变换：从右向左依次是：缩放，旋转，平移

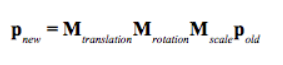
（4）同时绕3个轴进行旋转， 按照ZXY的顺序