CDH简介

article/2025/10/3 7:16:53

一、CDH概念

CDH，全称Cloudera's Distribution, including Apache Hadoop。由美国的Cloudera公司推出的大数据产品；CDH是基于稳定版本的Apache Hadoop构建而成，也是目前市场上应用比较广泛的大数据产品。

二、CDH架构

三、CDH优点

1.版本管理做的好

2. 版本更新速度快

3.集群搭建效率高

4.安全性高 

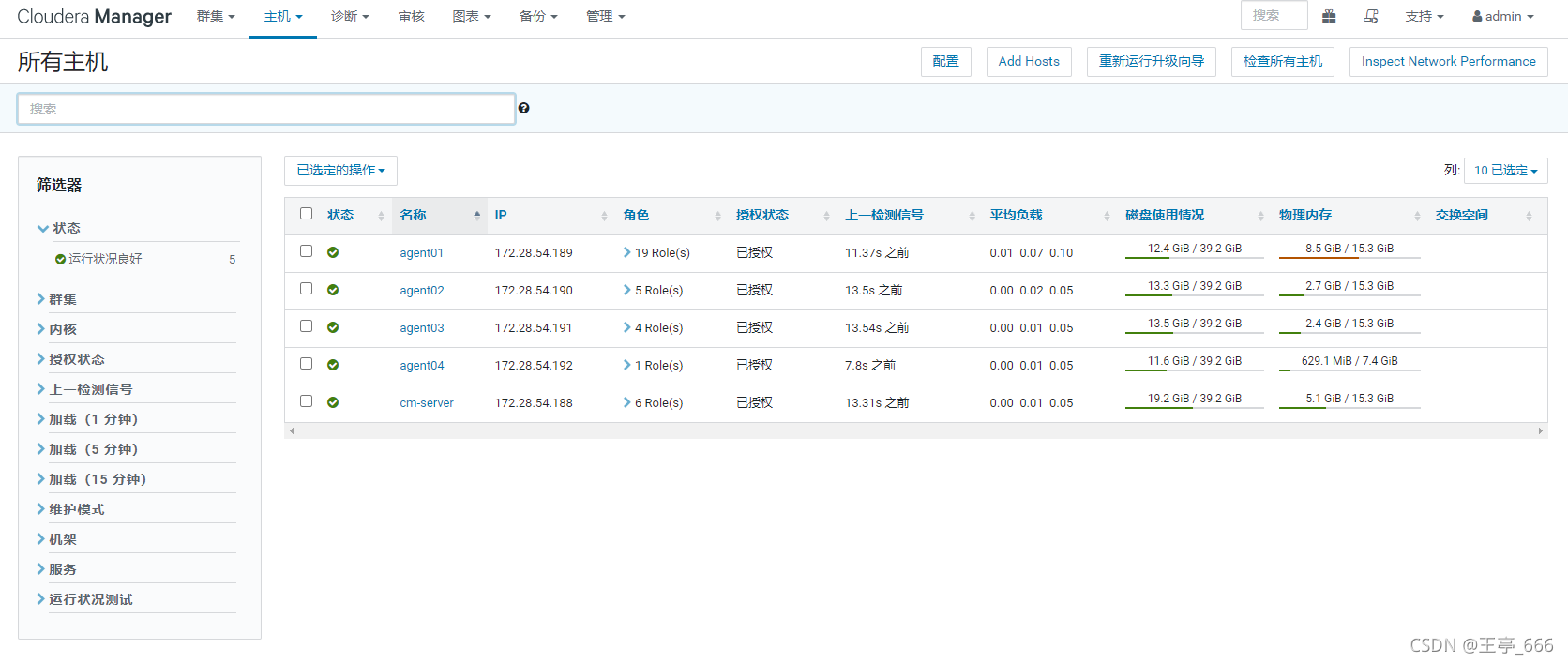
5.支持多种安装方式（Cloudera Manager方式）

    • Cloudera Manager

    • Yum

    • Rpm

    • Tarball


http://chatgpt.dhexx.cn/article/Y1cShPDF.shtml

相关文章

大数据之CDH（web页面部署Hadoop）

大数据之CDH（web页面部署Hadoop）

一、了解CDH 在众多 Hadoop 版本中， CDH 是 Hadoop 众多分支中比较出色的版本， 它由Cloudera 发行和维护。CDH 基于 Apache 的 Hadoop 进行重新构建，提供了基于 Web 页面的群集部署和管理操作。 1.1 Hadoop 属于开源软件，采用Apa…
阅读更多...
CDH简介及CDH部署、原理和使用介绍( 版本6.3.1 )

CDH简介及CDH部署、原理和使用介绍( 版本6.3.1 )

CDH简介及CDH部署、原理和使用介绍( 版本6.3.1 ) 第一章：CDH简介 CDH概念 ​ CDH是Cloudera的100％开源平台发行版，包括Apache Hadoop，专为满足企业需求而构建。CDH提供开箱即用的企业使用所需的一切。通过将Hadoop与十几个其他…
阅读更多...
Symmetric Eigenvalue Decomposition

Symmetric Eigenvalue Decomposition

求特征值求出s，如何求r 转载于:https://www.cnblogs.com/zzsama/p/10856126.html
阅读更多...
Eigenvalue and singular value

Eigenvalue and singular value

1. 特征值: A为方阵，v是A的特征向量。 λ是特征向量v对应的特征值。 一个矩阵的特征向量是一组正交向量。 其中Q是这个矩阵A的特征向量组成的矩阵； 一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量&#xff0…
阅读更多...
Part2 正交、行列式、特征值

Part2 正交、行列式、特征值

方阵的行列式determinant eigen values特征值 Determinants det A|A| 这三个性质定义了行列式： 1. det I1 2. exchange rows：reverse sign of det 置换矩阵 det P1 even -1 odd 3. matlab求行列式： pivot formula主…
阅读更多...
【线代NumPy】第八章 - 特征值和特征向量 | Eigenvalue and Eigenvector | 简述并提供代码

【线代NumPy】第八章 - 特征值和特征向量 | Eigenvalue and Eigenvector | 简述并提供代码

💬 例1： import numpy as npA = np.array([[2, 3], [3, -6]]) w1, V1 = np.linalg.eig(A) # 计算A的特征值和特征向量print("A的特征值： = ", w1) print("A的特征向量： = ", V1)B = np.array([[5,2,0], [2,5,0], [-3,4,6]]) w2, V2 = np.linalg.eig(…
阅读更多...
Householder transformation + QL to calculate eigenValue and eigenVectors of Hertian Matrix, cpu code

Householder transformation + QL to calculate eigenValue and eigenVectors of Hertian Matrix, cpu code

化Hertinan matrix eigen problem into a real symmetric matrix eigen problem: 原理： 与matlab的结果进行对比： A[ ... ( 3.0 0.0*j) (-2.0 -2.0*j) (-0.9 -0.9*j) (-0.5 -0.5*j); ... (-2.0 2.0*j) ( 4.0 0.0*j) ( 1.0 1.0*j) (-0.7…
阅读更多...
Truncated Power Method for Sparse Eigenvalue Problems

Truncated Power Method for Sparse Eigenvalue Problems

目录 算法k的选择\(x\)的初始化代码 抱歉，真的没怎么看懂，当然，估计和我现在没法静下心来好好看也有关系。 算法 想法非常非常简单吧，就是在原来幂法的基础上，每次迭代的时候再加个截断。当然，论文里给出了…
阅读更多...
R语言将向量数据按照行方式转化为矩阵数据（设置参数byrow为TRUE）、计算矩阵数据的特征值（eigenvalue）

R语言将向量数据按照行方式转化为矩阵数据（设置参数byrow为TRUE）、计算矩阵数据的特征值（eigenvalue）

R语言将向量数据按照行方式转化为矩阵数据（设置参数byrow为TRUE）、计算矩阵数据的特征值（eigenvalue） 目录 R语言将向量数据按照行方式转化为矩阵数据（设置参数byrow为TRUE）、计算矩阵数据的特征值&#x…
阅读更多...
Nonlinear Component Analysis as a Kernel Eigenvalue Problem

Nonlinear Component Analysis as a Kernel Eigenvalue Problem

目录 引kernel PCA kernel 的选择性质一些问题代码 Scholkopf B, Smola A J, Muller K, et al. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319. 引 普通的PCA将下式进行特征分解（用论文的话讲就是对…
阅读更多...
拉格朗日乘数法和KKT条件的直观解释

拉格朗日乘数法和KKT条件的直观解释

拉格朗日乘数法和KKT条件的直观解释 标签（空格分隔）： 机器学习 linbin 2018-05-10 Abstract 在SVM的推导中，最优化问题是其中的核心，这里我们简单介绍下最优化问题，特别是带有约束的最优化问题&#xff…
阅读更多...
[Math Algorithm] 拉格朗日乘数法

[Math Algorithm] 拉格朗日乘数法

https://www.cnblogs.com/maybe2030/p/4946256.html 阅读目录 1. 拉格朗日乘数法的基本思想2. 数学实例3. 拉格朗日乘数法的基本形态4. 拉格朗日乘数法与KKT条件 拉格朗日乘数法（Lagrange Multiplier Method）之前听数学老师授课的时候就是一知半解&…
阅读更多...
每天五分钟机器学习算法：拉格朗日乘数法和KKT条件

每天五分钟机器学习算法：拉格朗日乘数法和KKT条件

KKT条件 当我们要求一个函数的极值，同时还有两种类型的约束条件，一种约束条件是等式约束，另外一种约束是不等式约束： x是一个变量（n维，n个样本），我们想要找到使得f(x)最大的x，还要满足上面的约束。此时KKT条件就出来说话了，如果要想让x满足这个条件下的f(x)的最大…
阅读更多...
拉格朗日乘数法及python实现拉格朗日乘数法

拉格朗日乘数法及python实现拉格朗日乘数法

拉格朗日乘数法（Lagrange Multiplier Method）基本思想 作为一种优化算法，拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（nk&am…
阅读更多...
SVM（一）：拉格朗日乘数法详解

SVM（一）：拉格朗日乘数法详解

目录 what直观理解法高数书上的解法 学习SVM的过程中遇到了这个拉格朗日乘数法，之前学高数的时候也学过，不过看到视频里的直观理解法和高数书上的解法有些不同，于是在这里把这两种方法记录下来，也当做是一次理解的过程。 what 先…
阅读更多...
拉格朗日乘数法什么时候考虑端点？解得的点是什么？

拉格朗日乘数法什么时候考虑端点？解得的点是什么？

问题提出 2013年的真题有一道题是用拉格朗日乘数法只能求出来一个点，当时很费解，因此查阅相关资料后，对这部分的知识做一个小总结。 无条件极值和条件极值 首先，在求无条件极值的时候，我们求的是曲面上的极值点。 例…
阅读更多...
拉格朗日乘数法的原理，我用10幅图把它讲清楚

拉格朗日乘数法的原理，我用10幅图把它讲清楚

机器学习是一个目标函数优化问题，给定目标函数f，约束条件会有一般包括以下三类： 仅含等式约束仅含不等式约束等式和不等式约束混合型 当然还有一类没有任何约束条件的最优化问题 关于最优化问题，大都令人比较头疼，首先…
阅读更多...
java 获取随机数方法,java生成随机数的三种方法

java 获取随机数方法,java生成随机数的三种方法

随机数有三种生成方式： 1、通过Math.random()方法 2、通过System.currentTimeMillis()方法获取毫秒数 3、通过Random类 第一种：常用方法Math.random()方法，是获取0-1之间的double类型的小数，在通过int类型墙砖即可 示例&#xff1…
阅读更多...
Java生成随机数的方式

Java生成随机数的方式

目录 Random基础使用优缺点分析 SecureRandom基础使用 总结：持续更新 Random Random 类诞生于 JDK 1.0，它产生的随机数是伪随机数，也就是有规则的随机数。Random 使用的随机算法为 linear congruential pseudorandom number generator (LGC)…
阅读更多...
Java 生成随机数的 5 种方式，你知道几种？

Java 生成随机数的 5 种方式，你知道几种？

点击上方“码农突围”，马上关注 这里是码农充电第一站，回复“666”，获取一份专属大礼包 真爱，请设置“星标”或点个“在看” 作者：专职跑龙套链接：https://www.jianshu.com/p/2f6acd169202 1. Math.random(…
阅读更多...
推荐文章

Copyright @ 2022~2023