拉格朗日乘数法及python实现拉格朗日乘数法

article/2025/10/3 8:50:29

拉格朗日乘数法（Lagrange Multiplier Method）基本思想
作为一种优化算法，拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题？拉格朗日乘数法从数学意义入手，通过引入拉格朗日乘子建立极值条件，对n个变量分别求偏导对应了n个方程，然后加上k个约束条件（对应k个拉格朗日乘子）一起构成包含了（n+k）变量的（n+k）个方程的方程组问题，这样就能根据求方程组的方法对其进行求解。

维基百科：最优化解
在这里插入图片描述
绿线标出的是约束g(x,y)=c的点的轨迹。蓝线是f(x,y)的等高线。箭头表示斜率，和等高线的法线平行。
从梯度的方向上来看，显然有d1>d2。绿色的线是约束，也就是说，只要正好在这条绿线上的点才可能是满足要求的点。如果没有这条约束，f(x,y)的最小值应该会落在最小那圈等高线内部的某一点上。加上了约束之后，最小值点显然应该是在f(x,y)的等高线正好和约束线相切的位置，因为如果只是相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小，只有到等高线与目标函数的曲线相切的时候，可能取得最优值。
如果我们对约束也求梯度∇g(x,y)，则其梯度如图中绿色箭头所示。很容易看出来，要想让目标函数f(x,y)的等高线和约束相切，则他们切点的梯度一定在一条直线上(f和g的斜率平行)。
也即在最优化解的时候：∇f(x,y)=λ（∇g(x,y)-C) （其中∇为梯度算子; 即：f(x)的梯度 = λ* g(x)的梯度，λ是常数,可以是任何非0实数，表示左右两边同向。）
即：▽[f(x,y)+λ(g(x,y)−c)]=0λ≠0
那么拉格朗日函数： F(x,y)=f(x,y)+λ(g(x,y)−c) 在达到极值时与f(x,y)相等，因为F(x,y)达到极值时g(x,y)−c等于零。
min( F(x,λ) )取得极小值时其导数为0，即▽f(x)+▽∑ni=λihi(x)=0，也就是说f(x)和h(x)的梯度共线。
简言之，在F(x,λ)取得最优化解时，即F(x,λ)取极值（导数为0，▽[f(x,y)+λ(g(x,y)−c)]=0）时，f(x)与g(x) 梯度共线，此时就是在条件约束g(x)下，f(x)的最优化解。

例子

给定椭球，式子如下所示。求这个椭球的内接长方体的最大体积。
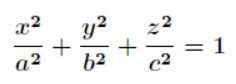
在这里插入图片描述
这个问题实际上就是条件极值问题，即在题目条件下，求解 f（x，y，z）=8xyz的最大值。

先根据条件消去 z，然后带入转化为无条件极值问题来处理。但是有时候这样做很困难，甚至是做不到的，这时候就需要用拉格朗日乘数法了。通过拉格朗日乘数法将问题转化为
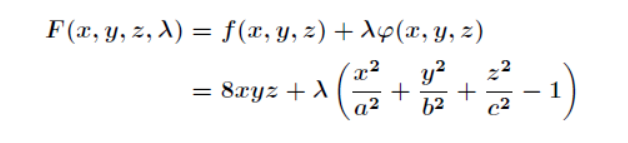
在这里插入图片描述
接着，要对**F(x，y，z，λ)**求偏导得到

联立前三个方程得到：bx=ay、az=cx，带入第四个方程求解得到

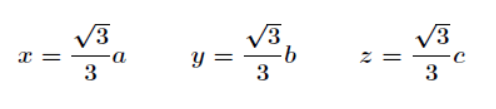
最后，带回原式求解得到最大值，如下所示。

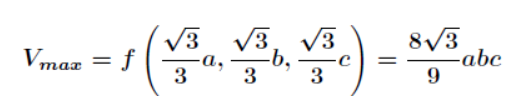
Python求解

题目同刚刚所求解的例子。

from scipy.optimize import minimize
import numpy as np
e = 1e-10 # 非常接近0的值
fun = lambda x : 8 * (x[0] * x[1] * x[2]) # f(x,y,z) =8 *x*y*z
cons = ({'type': 'eq', 'fun': lambda x: x[0]**2+ x[1]**2+ x[2]**2 - 1}, # x^2 + y^2 + z^2=1{'type': 'ineq', 'fun': lambda x: x[0] - e}, # x>=e等价于 x > 0{'type': 'ineq', 'fun': lambda x: x[1] - e},{'type': 'ineq', 'fun': lambda x: x[2] - e})
x0 = np.array((1.0, 1.0, 1.0)) # 设置初始值
res = minimize(fun, x0, method='SLSQP', constraints=cons)
print('最大值：',res.fun)
print('最优解：',res.x)
print('迭代终止是否成功：', res.success)
print('迭代终止原因：', res.message)