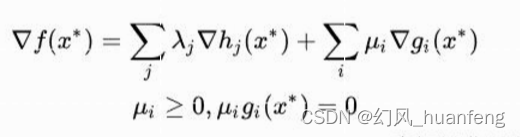1. 特征值:

A为方阵,v是A的特征向量。 λ是特征向量v对应的特征值。
一个矩阵的特征向量是一组正交向量。

其中Q是这个矩阵A的特征向量组成的矩阵;
一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。
Σ是一个对角阵,每一个对角线上的元素就是一个特征值,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向。
2. 奇异值:

A是一个N * M的矩阵,U是一个N * N的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个N * M的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V’(V的转置)是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量)。

A的转置乘A得到方阵。求方阵的特征值λ和特征向量v。 v为A的右奇异向量。


σ为奇异值,u为左奇异向量。奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,并且减少特别快。可用前面r大的奇异值来近似描述矩阵。

r<<m; r<<n. r越接近m,则右边结果越接近A。
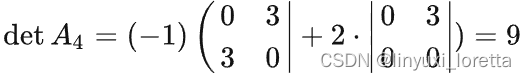





![[Math Algorithm] 拉格朗日乘数法](https://images2015.cnblogs.com/blog/764050/201511/764050-20151108125844430-1838900179.png)