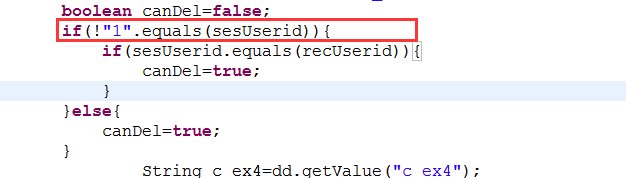
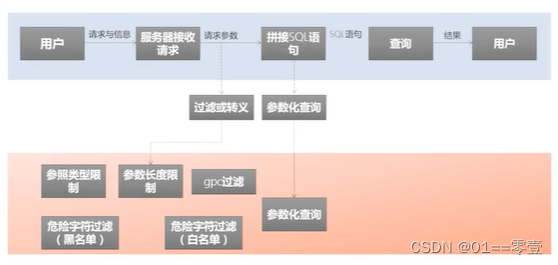
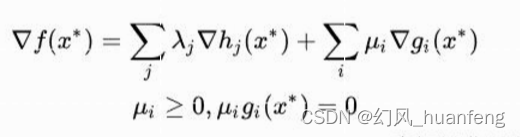---

 💬 例1：

import numpy as npA = np.array([[2, 3], [3, -6]])
w1, V1 = np.linalg.eig(A) # 计算A的特征值和特征向量print("A的特征值： = ", w1)
print("A的特征向量： = ", V1)B = np.array([[5,2,0], [2,5,0], [-3,4,6]])
w2, V2 = np.linalg.eig(B) # 计算B的特征值和特征向量print("\n");
print("B的特征值 = ", w2)
print("B的特征向量 = ", V2)

🚩 运行结果：

A的特征值： =  [ 3. -7.]
A的特征向量： =  [[ 0.9486833  -0.31622777]
 [ 0.31622777  0.9486833 ]]

B的特征值 =  [6. 7. 3.]
B的特征向量 =  [[ 0.          0.57735027  0.36650833]
 [ 0.          0.57735027 -0.36650833]
 [ 1.          0.57735027  0.85518611]]

💬 例2：

url：htt