Nonlinear Component Analysis as a Kernel Eigenvalue Problem

目录

• 引
• kernel PCA
  • kernel 的选择
  • 性质
  • 一些问题
• 代码

Scholkopf B, Smola A J, Muller K, et al. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319.

引

普通的PCA将下式进行特征分解（用论文的话讲就是对角化）：
\[ C = \frac{1}{M} \sum \limits_{j=1}^M x_j x_j^T \]
其中\(x_j \in \mathbb{R}^{N}, j = 1, \ldots, M\)，且\(\sum \limits_{j=1}^M x_j = 0\)(中心化)。

而kernel PCA试图通过一个非线性函数：
\[ \Phi:\mathbb{R}^N \rightarrow F, x \rightarrow X \]
其中\(F\)是一个高维空间（甚至是无限维)。
所以我们要解决这么一个问题：
\[ \bar{C} = \frac{1}{M} \sum_{j=1}^M \Phi (x_j) \Phi(x_j)^T \]

其实我们面对的第一个问题不是维度的问题而是\(\Phi\)的选择或者说构造。我们为什么要把数据映射到高维的空间？因为当前数据的结构（或者说分布）并不理想。

比如满足\((x-1)^2+(y-1)^2=4\)的点，我们可以扩充到高维空间\((x^2, x, y, y^2)\)，在高维空间是线性的（虽然这个例子用在kernel SVM 比较好）。

因为\(\Phi(\cdot)\)的构造蛮麻烦的，即便有一些先验知识。我们来看一种比较简单的泛用的映射：
\[ (x_1, x_2, x_3) \rightarrow (x_1^3, x_2^3, x_3^3, x_1^2x_2,x_1^2x_3,x_1x_2^2,x_1x_3^2,x_2^2x_3,x_2x_3^2,x_1x_2x_3) \]
这种样子的映射，很容易把维度扩充到很大很大，这个时候求解特征问题会变得很麻烦。

kernel PCA

假设\(\sum \limits_{i=1}^M \Phi(x_i)=0\)(如何保证这个性质的成立在最后讲，注意即便\(\sum \limits_{i=1}^M x_i = 0\)，\(\sum \limits_{i=1}^M \Phi(x_i)=0\)也不一定成立)。

假设我们找到了\(\bar{C}\)的特征向量\(V \ne 0\):
\[ \bar{C}V = \lambda V \]
因为\(V\)是\(\Phi(x_i),i=1,\ldots, M\)的线性组合（这个容易证明），所以，\(V\)可以由下式表示：
\[ V = \sum \limits_{i=1}^M \alpha_i \Phi(x_i) \]

所以：
\[ \lambda V^T \Phi(x_j) = V^T\bar{C} \Phi(x_j), \quad for \: all \: j=1,\ldots, M \]
等价于(记\(\Phi = [\Phi(x_1), \ldots, \Phi(x_M)]\))：
\[ \begin{array}{ll} \lambda \sum \limits_{i=1}^M \alpha_i (\Phi^T(x_i)\Phi(x_j)) &= \lambda \{ \Phi^T \Phi(x_j)\} ^T \alpha \\ & =\frac{1}{M} \sum \limits_{i=1}^M \alpha_i \Phi^T(x_i) \Phi \Phi^T \Phi(x_j) \\ & = \frac{1}{M} \{\Phi^T \Phi \Phi^T \Phi(x_j)\}^T \alpha \end{array} \]
对于\(j=1,\ldots, M\)均成立，其中\(\alpha = [\alpha_1, \ldots, \alpha_M]^T\)。

等价于：
\[ M \lambda \Phi^T \Phi \alpha = \Phi^T \Phi \Phi^T \Phi \alpha \]
令\(K = \Phi^T \Phi\)，那么可写作：
\[ M \lambda K \alpha = K^2\alpha \]
其中\(K_{ij} = \Phi^T(x_i) \Phi(x_j)\)

所以，我们可以通过下式来求解\(\alpha\):
\[ M\lambda \alpha = K \alpha \]
即\(\alpha\)是\(K\)的特征向量(注意，当\(\alpha\)为特征向量的时候是一定符合\(M \lambda K \alpha = K^2\alpha\)的，反之也是的，即二者是等价的)。

假设\(\lambda_1 \ge \lambda_2 \ge \ldots \ge \lambda_M\)对应\(\alpha^1, \ldots, \alpha^M\)，那么相应的\(V\)也算是求出来了。

需要注意的是，\(\|\alpha\|\)往往不为1，因为我们希望\(\|V\|=1\)，所以：
\[ V^TV = \alpha^T K \alpha = \lambda \|\alpha\|^2 = 1 \]
所以\(\|\alpha\| = \frac{1}{\sqrt{\lambda}}\)

PCA当然需要求主成分，假设有一个新的样本\(x\)，我们需要求：
\[ \Phi(x)^TV = \Phi^T(x) \Phi \alpha = \sum \limits_{i=1}^M \alpha_i \Phi^T(x_i) \Phi(x) \]

注意，我们只需要计算\(\Phi^T(x_i) \Phi(x)\)。

现在回到kernel PCA 上的关键kernel上。注意到，无论是K，还是最后计算主成分，我们都只需要计算\(\Phi^T(x)\Phi(y)\)就可以了，所以如果我们能够找到一个函数\(k(x,y)\)来替代就不必显示将\(x\)映射到\(\Phi(x)\)了，这就能够避免了\(\Phi(\cdot)\)的选择问题和计算问题。

kernel 的选择

显然，PCA的\(\lambda \ge 0\)，所以我们也必须保证\(K\)为半正定矩阵，相应的核函数\(k\)称为正定核，Mercer定理有相应的构建。

也有现成的正定核：

多项式核

\[ k(x, y) = (x^Ty + 1)^d \]
论文中是\((x^Ty)^d\)

高斯核函数

\[ k(x, y) = \exp \{\ -\frac{\|x-y\|^2}{2\sigma^2}\} \]

性质

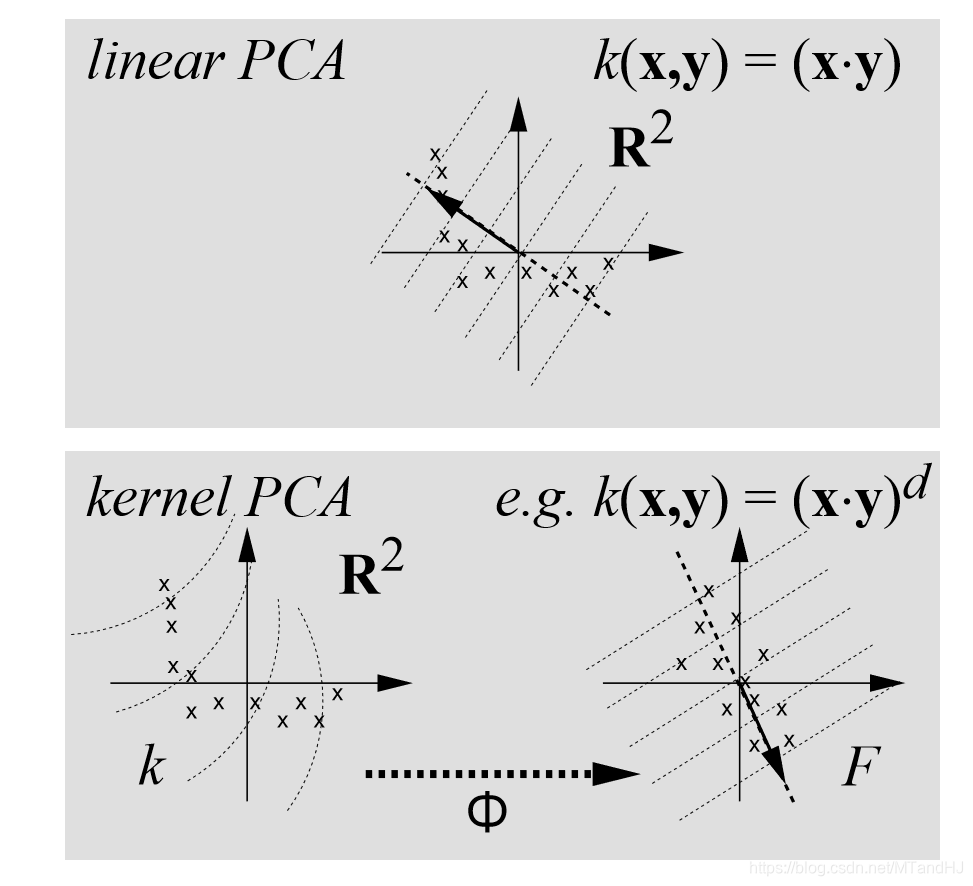
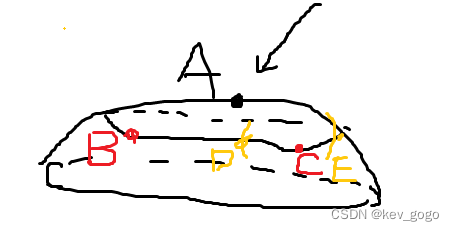
论文用上面的一个例子来说明，kernel PCA可能更准确地抓住数据的结构。

kernel PCA具有普通PCA的性质，良好的逼近（从方差角度），以及拥有最多的互信息等等。并且，如果\(k(x, y) = k(x^Hy)\)，那么kernel PCA还具有酉不变性。

因为普通的PCA处理的是一个\(N \times N\)的协方差矩阵，所以，至多获得\(N\)个载荷向量，而kernel PCA至多获得\(M\)个载荷向量(特征值非零)。所以，kernel PCA有望比普通PCA更加精准。

一些问题

中心化

PCA处理的是协方差矩阵，正如我们最开始所假设的，\(\sum \limits_{i=1}^{M} \Phi(x_i)=0\),即中心化。因为\(\Phi(\cdot)\)并不是线性函数，所以，即便\(\sum \limits_{i=1}^M x_i = 0\)也不能保证\(\sum \limits_{i=1}^{M} \Phi(x_i)=0\)，不过有别的方法处理。
令
\[ \tilde{\Phi}(x_i) = \Phi(x_i) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k) \\ \tilde{K}_{ij} = \tilde{\Phi}^T(x_i) \Phi(x_j) \\ 1_{M} = \{1\}_{ij}^{M \times M} \]
可以得到：
\[ \begin{array}{ll} \tilde{K}_{ij} &= \tilde{\Phi}^T(x_i) \Phi(x_j) \\ &= \big(\Phi(x_i) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k)\big)^T \big(\Phi(x_j) - \frac{1}{M}\sum \limits_{k=1}^M \Phi(x_k)\big) \\ &= K_{ij} - \frac{1}{M} \sum \limits_{k=1}^M K_{kj} - \frac{1}{M} \sum \limits_{k=1}^M K_{ik} + \frac{1}{M^2} \sum \limits \limits_{m,n=1}^M K_{mn} \\ &= (K - 1_MK - K1_M + 1_MK1_M)_{ij} \end{array} \]
于是，我们通过\(K\)可以构造出\(\tilde{K}\)。只需再求解\(\tilde{K}\tilde{\alpha} = M \lambda \tilde{\alpha}\)即可。

恢复

我们知道，根据PCA选出的载荷向量以及主成分，我们能够恢复出原数据（或者近似，如果我们只选取了部分载荷向量）。对于kernel PCA，比较困难，因为我们并没有显式构造\(\Phi(\cdot)\)，也就没法显式找到\(V\)，更何况，有时候我们高维空间找到\(V\)在原空间中并不存在原像。
或许， 我们可以通过：
\[ \min \limits_{x} \quad \|\Phi(x) - \Phi(\hat{x})\|^2 \]
来求解，注意到，上式也只和核函数\(k(x,y)\)有关。

代码

import numpy as npclass KernelPCA:def __init__(self, data, kernel=1, pra=3):self.__n, self.__d = data.shapeself.__data = np.array(data, dtype=float)self.kernel = self.kernels(kernel, pra)self.__K = self.center()@propertydef shape(self):return self.__n, self.__d@propertydef data(self):return self.data@propertydef K(self):return self.__K@propertydef alpha(self):return self.__alpha@propertydef eigenvalue(self):return self.__valuedef kernels(self, label, pra):"""数据是一维的时候可能有Bug:param label: 1:多项式;2:exp:param pra:1: d; 2: sigma:return: 函数 或报错"""if label is 1:return lambda x, y: (x @ y) ** praelif label is 2:return lambda x, y: \np.exp(-(x-y) @ (x-y) / (2 * pra ** 2))else:raise TypeError("No such kernel...")def center(self):"""中心化"""oldK = np.zeros((self.__n, self.__n), dtype=float)one_n = np.ones((self.__n, self.__n), dtype=float)for i in range(self.__n):for j in range(i, self.__n):x = self.__data[i]y = self.__data[j]oldK[i, j] = oldK[j, i] = self.kernel(x, y)return oldK - 2 * one_n @ oldK + one_n @ oldK @ one_ndef processing(self):"""实际上就是K的特征分解,再对alpha的大小进行一下调整"""value, alpha = np.linalg.eig(self.__K)index = value > 0value = value[index]alpha = alpha[:, index] * (1 / np.sqrt(value))self.__alpha = alphaself.__value = value / self.__ndef score(self, x):"""来了一个新的样本，我们进行得分"""k = np.zeros(self.__n)for i in range(self.__n):y = self.__data[i]k[i] = self.kernel(x, y)return k @ self.__alpha"""import matplotlib.pyplot as pltx = np.linspace(-1, 1, 100)
y = x ** 2 + [np.random.randn() * 0.1 for i in range(100)]
data = np.array([x, y]).Ttest = KernelPCA(data, pra=1)
test.processing()
print(test.alpha.shape)
print(test.alpha[:, 0])"""