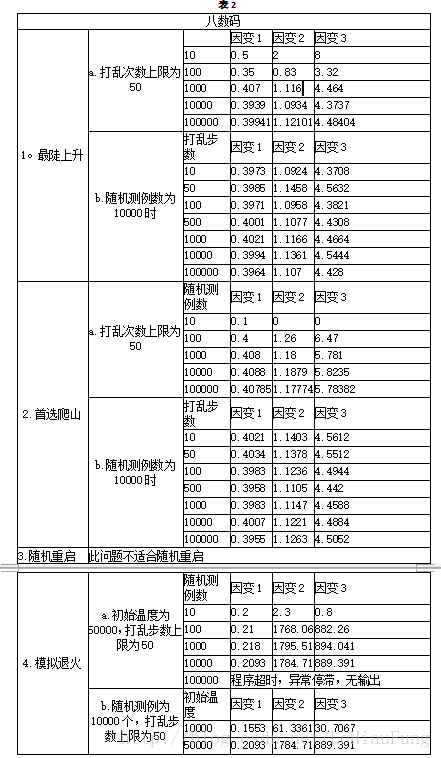
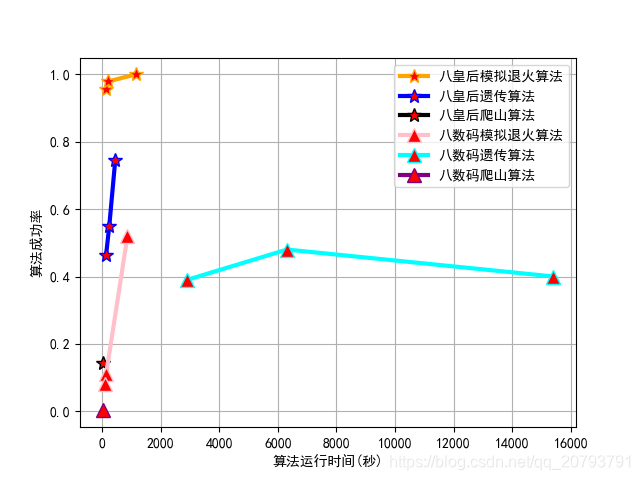
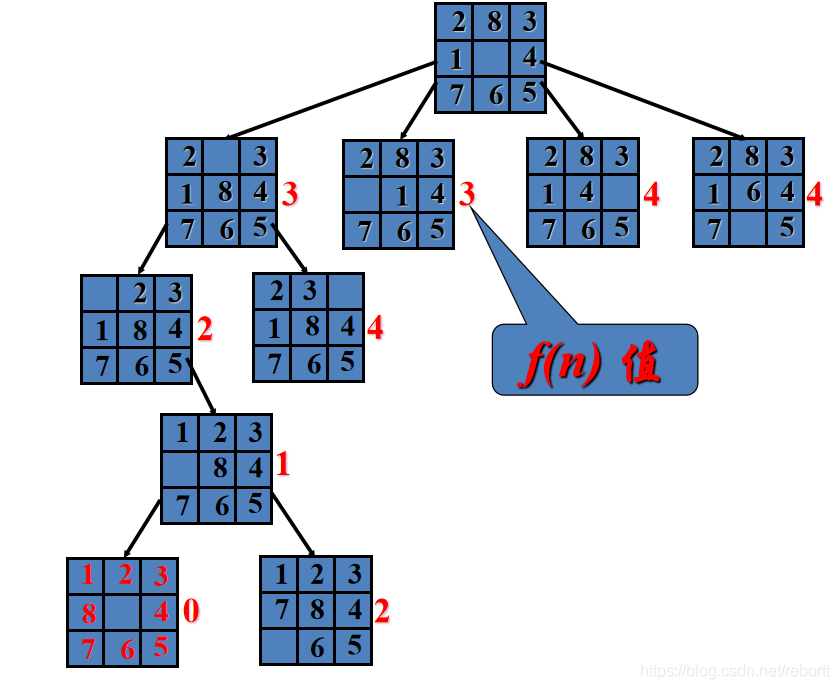
C语言局部算法求解八皇后问题
- 写在前面
- 八皇后问题及局部搜索算法
- 爬山法(hill-climbing searching)
- 算法介绍
- 代码实现
- 退火法(simulated annealing)
- 算法介绍
- 代码实现
- 遗传算法
- 算法介绍
- 代码实现
写在前面
该篇博客改自https://blog.csdn.net/chenxz_/article/details/83014641,习惯用python可以去参考他的代码。
八皇后问题及局部搜索算法
八皇后问题(英文:Eight queens),是由国际西洋棋棋手马克斯·贝瑟尔于1848年提出的问题,是回溯算法的典型案例。
问题表述为:在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转,和对角线对称变换的摆法看成一类,共有42类。计算机发明后,有多种计算机语言可以编程解决此问题。
局部搜索算法是一种简单的贪心搜索算法,是解决最优化问题的一种启发式算法,该算法每次从当前解的临近解空间中根据启发函数选择一个最优解(也不一定是最优解)作为当前解,直到达到一个局部最优解。本文以求解八皇后问题来描述爬山法,模拟退火法以及遗传算法。
爬山法(hill-climbing searching)
算法介绍
爬山法是指经过评价当前的问题状态后,限于条件去增加这一状态与目标状态的差异,经过迂回前进,最终达到解决问题的总目标。就如同爬山一样,为了到达山顶,有时不得不先上矮山顶,然后再下来,这样翻越一个个的小山头,直到最终达到山顶。可以说,爬山法是一种"以退为进"的方法,往往具有"退一步进两步"的作用,后退乃是为了更有效地前进。爬山法也叫逐个修改法、瞎子摸象法。
代码实现
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#include<string.h>//初始化八皇后的布局
int inital(int *status)
{int i,row;for(i=0;i<8;i++){row=rand()%8;status[i]=row;}return 0;
}//定义了两种方式展示八皇后布局
void display(int *status)
{int i;for(i=0;i<8;i++)printf("%d ",status[i]);printf("\n");/*for(i=0;i<8;i++){for(j=0;j<8;j++){if(status[i]!=j)printf("%d ",0);elseprintf("%d ",1);}printf("\n");}*/
}//得到八皇后有冲突的数目
int num_of_conflict(int *status)
{int num_of_conflict=0;int i,j;for(i=0;i<7;i++){for(j=i+1;j<8;j++){if((status[i]==status[j])||((j-i)==abs(status[i]-status[j])))num_of_conflict++;}}return num_of_conflict;
}//将一个八皇后布局拷贝给另一个
void copy(int *in, int *out)
{int i;for(i=0;i<8;i++)out[i]=in[i];
}//比较两个八皇后布局是否相同
int compare(int *status1,int *status2)
{int i;for(i=0;i<8;i++){if(status1[i]!=status2[i])return 0;}return 1;
}//改变布局,得到最小冲突的分布,即爬山的应用
int *get_min_conflict(int *status)
{int i,j,choose;int *min_status=(int*)malloc(sizeof(int)*9);memset(min_status,0,sizeof(int)*9);int new_status[8]={0};copy(status,min_status);for(i=0;i<8;i++){for(j=0;j<8;j++){copy(status,new_status);if(status[i]!=j){new_status[i]=j;if(num_of_conflict(new_status)<num_of_conflict(min_status))copy(new_status,min_status);else if(num_of_conflict(new_status)==num_of_conflict(min_status)&&num_of_conflict(new_status)!=num_of_conflict(status)){choose=rand()%2;if(choose==1)copy(new_status,min_status);}}}}return min_status;
}int main()
{int status[8]={0};int step=0,max_step=8;int *new_status=(int*)malloc(8*sizeof(int));memset(new_status,0,sizeof(int)*8);srand((unsigned)time(NULL));inital(status);printf("initual status:\n");display(status);printf("the num of conflict: %d\n\n",num_of_conflict(status));while(num_of_conflict(status)&&step<max_step){step++;new_status=get_min_conflict(status);;if(compare(new_status,status)){printf("the best answer:\n");display(status);printf("the num of conflict: %d\ncan not find an answer!\n",num_of_conflict(status));break;}copy(new_status,status);printf("the new status:\n");display(status);printf("the num of conflict: %d\n\n",num_of_conflict(status));if(num_of_conflict(status)==0)printf("find answer!\n");}getchar();return 0;
}
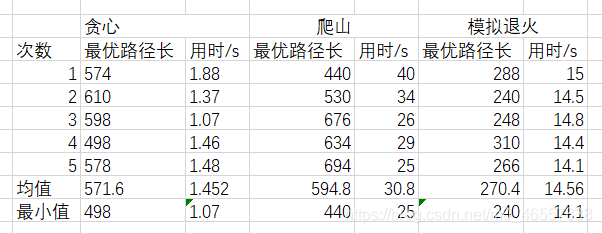
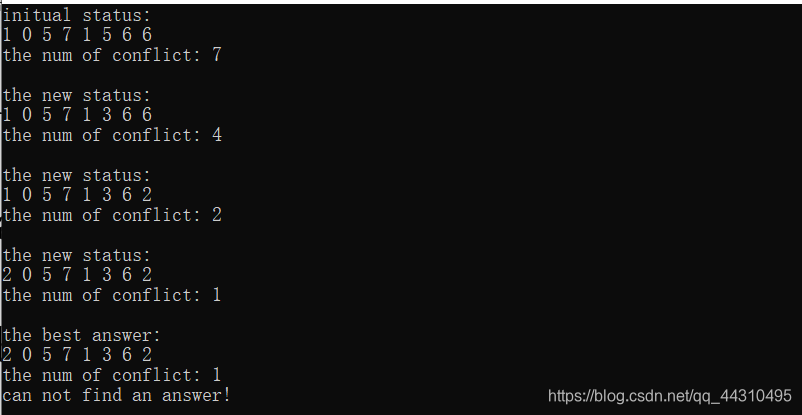
效果展示:
失败案例:
成功案例: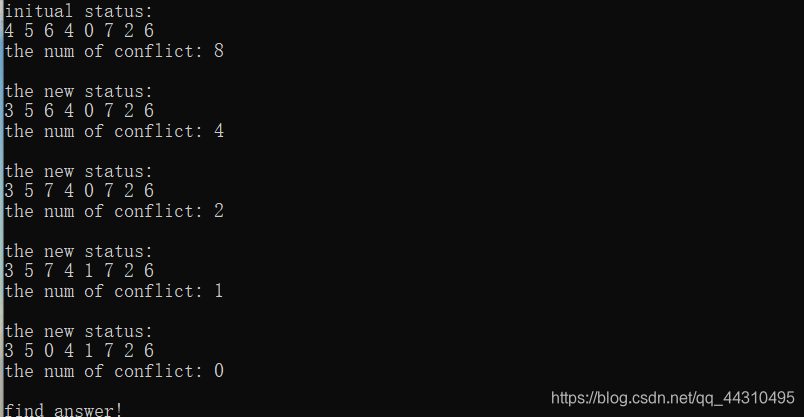
退火法(simulated annealing)
算法介绍
模拟退火算法(Simulated Annealing,SA)最早的思想是由N. Metropolis [1] 等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法,理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用,诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。
代码实现
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#include<string.h>int inital(int *status)
{int i,j;for(i=0;i<8;i++){j=rand()%8;status[i]=j;}return 0;
}void display(int *status)
{int i;for(i=0;i<8;i++)printf("%d ",status[i]);printf("\n");/*for(i=0;i<8;i++){for(j=0;j<8;j++){if(status[i]!=j)printf("%d ",0);elseprintf("%d ",1);}printf("\n");}*/
}int num_of_conflict(int *status)
{int num_of_conflict=0;int i,j;for(i=0;i<7;i++){for(j=i+1;j<8;j++){if((status[i]==status[j])||((j-i)==abs(status[i]-status[j])))num_of_conflict++;}}return num_of_conflict;
}void copy(int *in, int *out)
{int i;for(i=0;i<8;i++)out[i]=in[i];
}int compare(int *status1,int *status2)
{int i;for(i=0;i<8;i++){if(status1[i]!=status2[i])return 0;}return 1;
}//获取下一个布局,随机的
int *get_next_status(int *status, double T)
{ int i,j;int flag=0;int choice;int new_status[8]={0};int **next_status=(int**)malloc(sizeof(int*)*56);for(i=0;i<56;i++){next_status[i]=(int*)malloc(sizeof(int)*9);memset(next_status[i],0,sizeof(int)*9);}for(i=0;i<8;i++){for(j=0;j<8;j++){copy(status,new_status);if(status[i]!=j){new_status[i]=j;copy(new_status,next_status[flag++]);} }}choice=rand()%56;if(num_of_conflict(next_status[choice])<=num_of_conflict(status)){return next_status[choice];}else{double E=num_of_conflict(status)-num_of_conflict(next_status[choice]);double probability=exp(E/T);double choose=(double)(rand()%999)/1000.0;if(choose<=probability){return next_status[choice];}}return status;
}int main()
{double T=5.0;int*status=(int*)malloc(sizeof(int)*9);memset(status,0,sizeof(int)*9);int*new_status=(int*)malloc(sizeof(int)*9);memset(new_status,0,sizeof(int)*9);srand((unsigned)time(NULL));inital(status);printf("the initial status:\n");display(status);printf("the num of conflict: %d\n\n",num_of_conflict(status));while(num_of_conflict(status)){new_status=get_next_status(status,T);if(compare(new_status,status)) printf("it does not move\n");else{copy(new_status,status);printf("the new status:\n");display(status);printf("the num of conflict: %d\n\n",num_of_conflict(status));if(num_of_conflict(status)==0)printf("find answer!\n");}T=T*0.99;if(T<0.0001){printf("max try, can not find an answer\n");break;}}getchar();return 0;
}
一般来说爬山法都能得到成功布局
代码效果:
遗传算法
算法介绍
遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
代码实现
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#include<string.h>int inital(int *status)
{int i,j;for(i=0;i<8;i++){j=rand()%8;status[i]=j;}return 0;
}void display(int *status)
{int i;for(i=0;i<8;i++)printf("%d ",status[i]);printf("\n");/*for(i=0;i<8;i++){for(j=0;j<8;j++){if(status[i]!=j)printf("%d ",0);elseprintf("%d ",1);}printf("\n");}*/
}//展示种群所有布局
void display_all(int**all_status)
{int i;for(i=0;i<4;i++){display(all_status[i]);}
}//展示种群中各布局的冲突,调试的时候用的,代码运行不需要
void display_noConflict(int *noConflict)
{int i;for(i=0;i<4;i++){printf("%d ",noConflict[i]);}printf("\n");
}int num_of_conflict(int *status)
{int num_of_conflict=0;int i,j;for(i=0;i<7;i++){for(j=i+1;j<8;j++){if((status[i]==status[j])||((j-i)==abs(status[i]-status[j])))num_of_conflict++;}}return num_of_conflict;
}//得到种群中最小的冲突数
int get_minConflict(int **all_status)
{int min=999;int i;for(i=0;i<4;i++){if(num_of_conflict(all_status[i])<min)min=num_of_conflict(all_status[i]);}return min;
}int num_of_noConflict(int*status)//我也不知道为什么要定义这个函数,有num_of_conlict好像就够了
{return 28-num_of_conflict(status);
}void copy(int *in, int *out)
{int i;for(i=0;i<8;i++)out[i]=in[i];
}int compare(int *status1,int *status2)
{int i;for(i=0;i<8;i++){if(status1[i]!=status2[i])return 0;}return 1;
}//获得种群中所有个体冲突数集合
int get_sum(int*num)
{int i;int sum=0;for(i=0;i<4;i++)sum+=num[i];return sum;
}//随机返回种群中四个个体中的一个
int *get_parent(int**all_status,int*noConflict) //我也不知道为什么要这么写,完全可以直接调用rand()返回0到3的随机数,可能是为了看起来更像遗传吧
{int choice=rand()%get_sum(noConflict);if(choice<noConflict[0])return all_status[0];else if(choice>=noConflict[0]&&choice<(noConflict[0]+noConflict[1]))return all_status[1];else if(choice>=(noConflict[0]+noConflict[1])&&choice<(noConflict[0]+noConflict[1]+noConflict[2]))return all_status[2];return all_status[3];
}//种群中个体随机变异
int **variation(int **all_status)
{int i,col,row;for(i=0;i<4;i++){row=rand()%8;col=rand()%8;all_status[i][row]=col;}return all_status;
}//种群中个体遗传
int **inheritance(int **all_status)
{int flag=0;int i,j,num;int *father,*mother;int child1[8]={0};int child2[8]={0};int *noConflict=(int*)malloc(sizeof(int)*5);memset(noConflict,0,sizeof(int)*5);int **new_all_status=(int**)malloc(sizeof(int*)*4);for(i=0;i<4;i++){new_all_status[i]=(int*)malloc(sizeof(int)*9);memset(new_all_status[i],0,sizeof(int)*5);noConflict[i]=num_of_noConflict(all_status[i]);}for(i=0;i<2;i++){father=get_parent(all_status,noConflict);mother=get_parent(all_status,noConflict);while(compare(father,mother))mother=get_parent(all_status,noConflict);copy(father,child1);copy(mother,child2);num=rand()%7;for(j=0;j<num+1;j++){child1[j]=child2[j];child2[j]=father[j];}copy(child1,new_all_status[flag++]);copy(child2,new_all_status[flag++]);}return new_all_status;
}//种群中是否有成功布局
int find_answer(int**all_status)
{int i;for(i=0;i<4;i++){if(num_of_noConflict(all_status[i])==28){printf("find answer!\n");display(all_status[i]);return 1;}}return 0;
}int main()
{int i;srand((unsigned)time(NULL));int **all_status=(int**)malloc(sizeof(int*)*4);for(i=0;i<4;i++){all_status[i]=(int*)malloc(sizeof(int)*9);memset(all_status[i],0,9);inital(all_status[i]);}printf("the inital all_status:\n");display_all(all_status);printf("the min all_status: %d\n\n",get_minConflict(all_status));all_status=inheritance(all_status);int vari_prob;while(!find_answer(all_status)){vari_prob=rand()%11;if(vari_prob==1){all_status=variation(all_status);printf("have a variation, and the all_status:\n");display_all(all_status);printf("the min conflict: %d\n\n",get_minConflict(all_status));}else{all_status=inheritance(all_status);printf("the next all_status:\n");display_all(all_status);printf("the min conflict: %d\n\n",get_minConflict(all_status));}}
}
代码效果展示(目前还在演化):