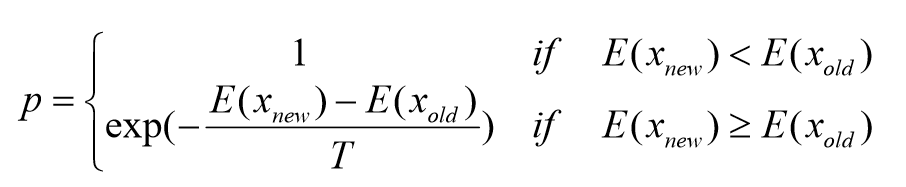一、TSP问题

1、TSP问题描述
简单来说，就是给定一些点，找出一条通过所有点的回路，使得回路最短

旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

2、本文使用的TSP例子
……为简化问题，直接在x轴上找一百个整数点 ，纵轴为0，横轴为1……100
显然最短路径是按照123456……100的顺序或者倒序走，再连接首位1和100，总路径为200
但在实际问题中，点的分布是不十分不规则的，比如中国各省的省会城市，绕着走一圈，是不可能直接就能看出路径最短的走法的。
……遍历所有的走法再求出每一条路径长度进行比较是一种易于理解的方法，但所有走法总数目是 城市个数的全排列，如果有N个城市，就有N！种走法。对于中国三十多个省来说，这不是一个很大的数字，可以遍历出，但是如果N很大，比如遍历中国所有乡镇，这是一个天文数字，一般计算机是很难以计算出来的。
……于是，为了减少计算代价，就可以利用贪心法、爬山法、模拟退火法来求解，当然求得的解达到全局最优解是很难的，但可以在一定误差范围内得到较优的解，计算代价却小得多。他们都带有一定的随机性，达不到全局最优解的原因是他们陷入局部最优解的凹槽中无法解脱出来。

二、简单介绍：贪心法、爬山法、模拟退火

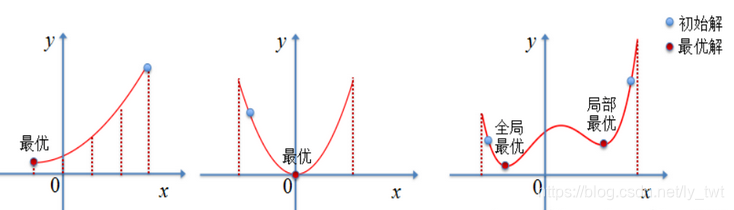
找到全局最优解就是找到全局最小解，全局最小的解肯定是在“凹槽”，一个函数可能有许许多多的“凹槽”，最小解是在找到最深的一个“凹槽”并取到它的底部的值。一般在未知的情况下，因为不知道最深“凹槽”是在哪里，只能随机选择一个点开始进行搜索，这三种方法都是随机选择一个点开始，按照“下山”方向进行搜索和更新

图中画的是一维，实际问题是二维以上的，以二维为例，二维寻找“凹槽”就和实际中下山的过程是一样的了，以下按照“下山”进行算法比喻的解释
1、贪心算法：
……在山坡上某一点时，随机确定一个方向，不管山坡的陡峭程度，如果这个方向是下山的方向，就要往这个方向走一步；如果这个方向是上山，就不走动，再随机确定一个方向。比如，一个人下山时，他身前180度角度内都是下山方向，身后180度角度内都是上山方向，在每一次确定方向时，只要方向是身前的180度之内，就往下走，如果方向是身后的180度之内，就不走。
……这种方法取名为贪心法，是因为它只着眼于眼前，目光短浅地对选取到的下山方向很贪心

2、爬山算法
……爬山法是贪心算法的一种升级，他每走一步之前，随机确定很多方向，如果是身前180度角度的方向都保留，身后180度的方向都舍弃，再从保留下来的方向中找一个最好的；也就是说，他的每一步不仅是下山的，而且是当前下山最快的方向。爬山法相对于贪心法来说，没有这么贪心于眼前找到的第一个下山方向，而是花一些时间找很多方向，再在这些方向中找一个最优的，然后才往下走一步

3、模拟退火算法
……首先，先说明一下，贪心算法和爬山算法都只能找到附近的局部最优解；显然，当它找到第一个山谷时，身前180度和身后180度都是上山的方向了，所以它不在变动。如果刚好，这个山谷是全部山谷中最深的一个，那么恭喜，找到了全部最优解了，当然，这种情况的概率不高，因为实际中的函数里面山谷非常多，随机初始点在最深山谷的附近是不容易的。
……模拟退火算法就是为了弥补以上两种方法只能找到局部最优解的缺点而发明的。因为前两种方法，每一步总是向着附近的山谷方向移动的，这就决定它们只能找到附近的山谷；模拟退火方法摒弃了这种“只向某一山谷方向移动的原则”，适当地向上山方向移动，这样它就有机会去见到更多的山谷，而找到更好的一个解。
……模拟退火取名如此，是因为它类于比物理学中的晶体熔化和降温。想要获取某种晶体的最佳状态，需要先熔化晶体再进行降温，在降温过程中不是一直保持降温状态，而是适当的给晶体深温。降温就好比下山，升温就好比上山。

4、路径变更、判断下山方向以及什么时候可以适当上山
1）路径变更
……路径也就是点的排列，装在一个数组中，排列顺序就是路径顺序（注意，最后一个要记得和第一个相连构成回路）。每一个数组排列代表一个路径，每次随机做一个小改动，就是将数组排列中的任意两个点交换位置，位置交换后就得到一个新的数组排列，也就是一个新的路径（当然也有其他路径变更的方法，只要变换数组的排列顺序即可，比如找到任意一个点，这个点前面的和后面的交换一下）
2）判断是否为下山方向
……变更前的路径为path_old,变更后的为path_new,求两次路径的长度len_old和len_new，若det=len_new-len_old，如果det<0，即为下山方向；此时对于贪心算法，会更新path_old为path_new作为下一次搜索起点
3）模拟退火法的适当上山原则
……给定温度T，这个T是为了模拟退火方法额外添加的，与寻找最优值没有直接关系；T会随着时间t不断衰退（有很多种已经给定好的衰退方法）,当T小于某个给定的值时，退火完毕。
……T每衰退一次，进行一次优化搜索，此时T的作用就是为优化搜索提供一个参数；优化搜索是一个循环过程：

(1)对T时刻的路径path_old，随机交换数组排列的两个位置得到一个新路径path_new，计算det=path_new-path_old
给一个概率p定义如下：path_old会有p的概率转变未path_new
(2)如果det<0,更新path_old为path_new作为下一次搜索起点，即p=1
(3)如果det>=0，计算p，p和det有关：
…………………………………p=exp(-det/T)
（其中(2)(3)称为 Metropolis准则，由退火过程而得，在退火过程det是能量差，在这里是路径长的差）

(4)对于det>0，可以看出，det越小，p越大，path_old转变的几率越大；det越大，p越小，path_old转变几率越小。p的直观意义就是，现在找到一个方向是上山的，要不要往这个方向走，往这个方向走的可能性是p
(5)计算得到p后，如何发挥p的作用？ 再随机产生一个（0-1）的随机数p_test，p_test小于p的几率就是p；所以，当p_test<p时，就将path_old变为path_new，尽管现在是上山方向

……在每一个T下，循环次数达到指定次数后跳出循环，最后的path保存下来（作为下一次循环的起点），T根据给定的方式下降成新的T，再进行循环……一直这样反复操作到T小于某个给定的值T_end
……如何选定初始T和T_end？可以根据一些启发经验来给定或者自己调比较，一般来说，初始T越高，运行时间越久，得到更优解的机会更高

三、python代码实现

1、初始路径：
由于我这里为了好理解，只取了x轴1-100这100个点，其最短路径就是按1到100顺序或者倒序走，再连接100和1，总共200
假装我们是不知道最优路径的，只能迷茫地随机选择某个路径作为初始路径，我利用random.shuffle（）函数随机打乱了1-100的排列，得到如下路径作为初始路径

# coding:utf-8
import random
import numpy as np
import timepath0= [47,  70,  68,  11,  36,  74,  81,  71,  86,  76,  34,  77,  80,85,  19,  49,  84,   2,  98,  20,  67,  13,  58,  33,  99,  44,66,  35,  30,   3,  56,  18,   1,  93,   9,  32,  12,  40,  90,51,  23, 100,  53,  59,  73,  22,  65,  97,  52,  64,  92,  72,17,  14,  31,  69,  50,   4,  78,  89,  57,  55,  45,  82,  10,28,  96,  91,  87,  42,   7,  83,  46,  61,   5,  29,  39,  21,88,  79,  26,  62,  27,  25,   8,  48,  94,  54,  24,  63,  43,75,  41,  15,  16,  95,  38,  60,  37,   6]

2、计算路径长
两个相邻点的路径长就是前后两个数的差的绝对值，总路径长就是将这些绝对值求和：

def path_len(path):path_dis = 0for i in range(len(path) - 1):two_dis = abs(path[i + 1] - path[i])  # 两点距离path_dis += two_dispath_dis += abs(path[-1] - path[0]) # 再加上首尾距离return path_dis

3、路径变换

def change_path(path, i, j):path_new=[]for t in path:path_new.append(t)c = path_new[i]path_new[i] = path_new[j]path_new[j] = creturn path_new

4、贪心法选择路径

def tanxin(path):n = len(path)get_new_path = pathold_len = path_len(path)count = 0while count < n*n:i = random.randint(0, n - 1)j = random.randint(0, n - 1)path_new = change_path(path, i, j)count += 1if path_len(path_new) < old_len:get_new_path = path_newbreakif get_new_path == path:print('没有找到附近更优解，返回原解')return pathelse:print('找到该path更优附近解，返回更优附近解：',get_new_path)return get_new_path

5、爬山法选择路径

def pashan(path):n = len(path)get_new_path = pathold_len = path_len(path)count = 0while count < n*n:i = random.randint(0, n - 1)j = random.randint(0, n - 1)path_new = change_path(path, i, j)count += 1if path_len(path_new) < old_len:old_len=path_len(path_new)get_new_path=path_newif get_new_path == path:print('没有找到附近更优解，返回原解')return pathelse:print('找到该path更优附近解，返回更优附近解：',get_new_path)return get_new_path

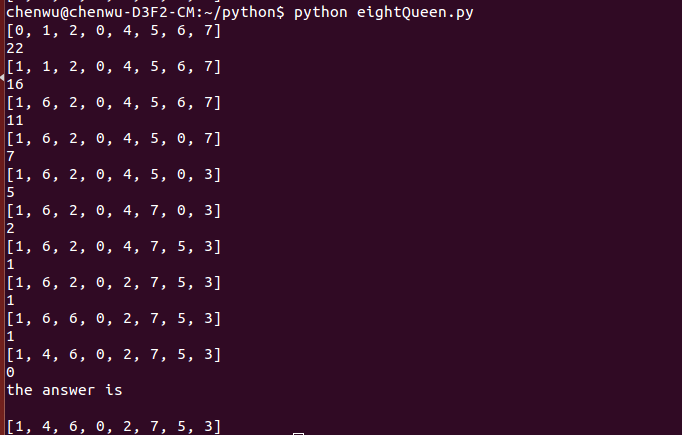
6、寻找最优解，当找不到下山方向（路径没有变化时）得到该种方法最优解

def best_path(path):nums=0while 1:path_better=tanxin(path)   #这里是用贪心法，改为pashan(path)则为爬山法nums+=1print(nums)if path_better == path:dis=path_len(path_better)print('----'*50)print( '共迭代',nums,'次，搜索到这种方法的最优解')print('最优路径：',path_better)print('最优距离：',dis)breakelse:path=path_better

7、模拟退火法（另开一个新程序）

# coding:utf-8
import math
import random# 温度变化函数
def T_update(t,T0):  # t 为推移时间，即每需要更新一次，t+1，表示冷却一次T=T0/math.log(1+t)return T# 计算路径长函数
def path_len(path):path_dis = 0for i in range(len(path) - 1):two_dis = abs(path[i + 1] - path[i])  # 两点距离path_dis += two_dispath_dis += abs(path[-1] - path[0])return path_dis# 得到新路径函数
def change_path(path, i, j):path_new=[]for t in path:path_new.append(t)c = path_new[i]path_new[i] = path_new[j]path_new[j] = creturn path_new# metropolis 准则
def metropolis(path_old,path_new,T):len_new=path_len(path_new)len_old=path_len(path_old)detE=len_new-len_oldif detE<=0:p=1else:p=math.pow(math.e,-detE/T)return p# 退火法函数
def disfire(path,T=20000,T_end=0.0001,iteration=10000):# 参数： 初始路径，初始温度，结束温度，每个温度下的迭代次数n=len(path)t=0while T>=T_end:t +=1count=0  # 计数while count < iteration:count += 1i=random.randint(0,n-1)j=random.randint(0,n-1)path_new=change_path(path,i,j)p=metropolis(path,path_new,T)p_random=random.random()if p_random <= p: # 当 path_new 更优时，p=1 , p_random<=p必成立, 若path_new不优，则以一定概率p变成path_newpath=path_newprint('温度',T,'下的优解：',path)T=T_update(t,T)best=path_len(path)print('最优解为：',path)print('最优解长度：',best)path0= [47,  70,  68,  11,  36,  74,  81,  71,  86,  76,  34,  77,  80,85,  19,  49,  84,   2,  98,  20,  67,  13,  58,  33,  99,  44,66,  35,  30,   3,  56,  18,   1,  93,   9,  32,  12,  40,  90,51,  23, 100,  53,  59,  73,  22,  65,  97,  52,  64,  92,  72,17,  14,  31,  69,  50,   4,  78,  89,  57,  55,  45,  82,  10,28,  96,  91,  87,  42,   7,  83,  46,  61,   5,  29,  39,  21,88,  79,  26,  62,  27,  25,   8,  48,  94,  54,  24,  63,  43,75,  41,  15,  16,  95,  38,  60,  37,   6]
disfire(path0)

其中 初始温度T和结束温度T_end可以不断调试择优
温度更新函数选择 经典退火函数

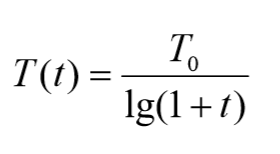
四、分别用这三种方法得出结果，进行比较

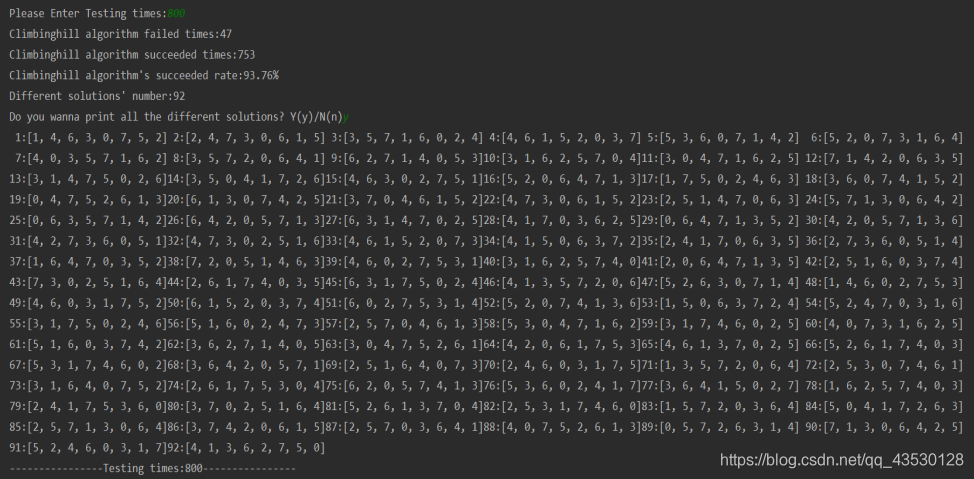
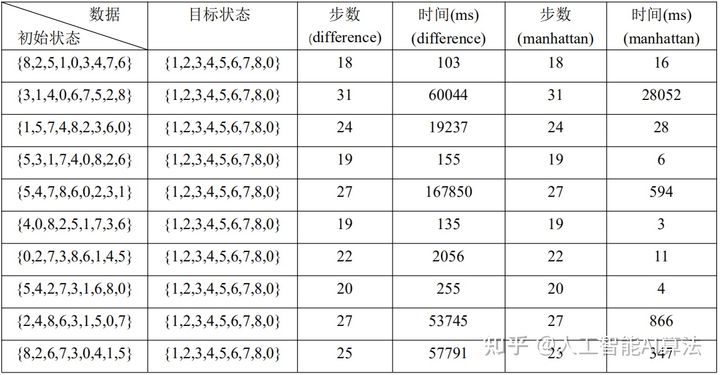
由于这三种方法的路径更新都有随机因素，所以每种方法运行五次得出结果进行观察与比较

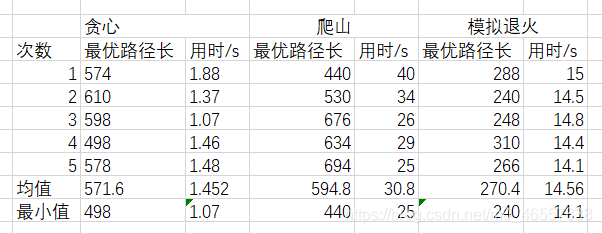
由表可见，
模拟退火法由于有自动跳出局部解的能力，而有更多地机会得到更优解；这种方法得到的优解远小于爬山法和贪心法，并且得到的优解波动并不大，耗时波动也不大
爬山法是相对比较耗时（依赖于每次搜索的迭代次数，由于我这里设置的比较多，所以爬山法过慢），但是得到的解并不一定优于贪心法，因为它每次都选取下山最快的路径，更容易陷入某些局部解；但它在一定几率上会获得比贪心法好很多的解
贪心法最易于理解最简单的方法，除了容易陷入局部解，好像没有什么其他缺点（随机效果也会产生一些缺点）