前言

爬山法和模拟退火都为随机化算法，考场想不到正解时可用来骗分，通常效果较好。模拟退火是基于爬山法的优化。

一、爬山法

爬山法是一种贪心算法，在有限时间内很快找到局部最优解，可用来求解单峰函数极值。

1.算法步骤

       随机选出一个点，每次向最大（最小）方向更新，直到找到极值位置。
        Q：为什么单峰函数不用三分？
        A：在多维问题中需要三分套三分求解，复杂度过高。

2.算法局限性

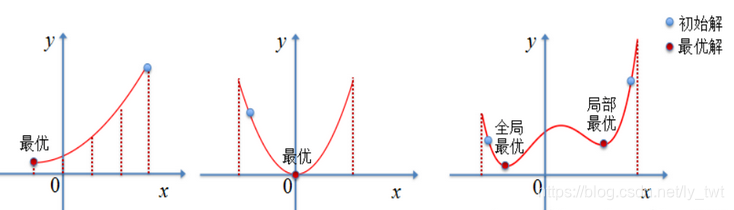
如下图所示：图片来源在这里插入图片描述
若当前问题的函数不是单峰，则爬山法只能寻找到局部最优解，不一定能寻找到全局最优解
下面的模拟退火能更好地解决此类问题。

二、模拟退火

模拟退火来源于物理模型———固体退火原理，是一种基于概率的算法。物理模型详细解释
通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法，能快速在有限集合中以较大的概率找到全局最优解。

1.算法步骤

        (1).定义温度T使之指数级别衰减（有些题可理解为步长）
              初始温度T₀         终止温度T_E
              衰减系数（0,1）一般取接近1的数
              衰减系数越接近1，衰减越慢

(2).随机选择一个点P，并计算出此点函数值

(3).每次迭代时在当前范围内随机选出一个新点NP，计算出NP函数值并与P函数值比较，定义 $\Delta$ E=f (NP)-f ( P )，若满足要求则由旧点跳到新点，否则以一定概率跳过去在这里插入图片描述
上图以求最小值为例

(4).随着温度降至终止温度，算法结束，找到全局最优解

(5).为提高准确率，将以上过程重复若干次

下图为算法运行过程
在这里插入图片描述

2.注意点

  (1).局限性：1.有时运行效率较低
                      2.有一定概率出错
  (2).要求：方案或函数空间具有一定连续性

3.例题

求费马点

题面：平面内有 n 个点，给出 n 个点的坐标，请你找出一个点，使得该点到这 n 个点的距离之和最小，答案四舍五入取整。

板子题，核心代码如下：

void simulate_anneal(){node now;now.x=randd(0,10000);//坐标范围边界now.y=randd(0,10000);for(double t=1e4;t>=1e-4;t*=0.99){//温度//初始温度：1e4  终止温度1e-4  衰减系数0.99node np;np.x=randd(now.x-t,now.x+t);np.y=randd(now.y-t,now.y+t);double delta=getans(np)-getans(now);//求解距离if(exp(-delta/t)>randd(0,1)){//以一定概率跳到新点now=np;}}
}int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%lf%lf",&a[i].x,&a[i].y);}for(int i=1;i<=100;i++){//多次迭代simulate_anneal();}printf("%.0lf\n",ans);return 0;
}

保龄球

题目链接模拟退火解决非几何问题

核心思路：
此题若用dp则状态难以存储，比较麻烦，转而发现本题空间有连续性（显然交换两个位置对答案影响并不大），因此可以每次随机交换两个位置，用模拟退火求解。

核心代码

void simulate_anneal(){for(double t=1e4;t>1e-4;t*=0.99){//温度 迭代int p=rand()%m;int q=rand()%m;int lst=getsum();//计算旧分数swap(a[p],a[q]);if(n+(a[n-1].x==10)==m){int now=getsum();//计算新分数int delta=now-lst;if(exp(delta/t)<(double)rand()/RAND_MAX){//一定概率交换swap(a[p],a[q]);}}else{swap(a[p],a[q]);}}
}int main(){n=read();for(int i=0;i<n;i++){a[i].x=read();a[i].y=read();}if(a[n-1].x==10){a[n].x=read();a[n].y=read();m=n+1;}else m=n;while((double)clock()/CLOCKS_PER_SEC<0.8){//卡时技巧simulate_anneal();}printf("%d\n",ans);return 0;
}

均分数据

题目链接

核心思路：
模拟退火+贪心求解
贪心思路：方差是一种表示数据离散程度的方法，只需要让这些数据之间的差值尽可能小，就可以保障方差最小，所以每次插入时找目前和最小的集合插入。

核心代码

double getans(){double aver=0,res=0;memset(s,0,sizeof s);for(int i=0;i<n;i++){int k=0;for(int j=0;j<m;j++){//贪心找目前和最小的集合if(s[k]>s[j]){k=j;}}s[k]+=a[i];//插入}for(int i=0;i<m;i++){aver+=(double)(s[i]/m);}for(int i=0;i<m;i++){res+=(s[i]-aver)*(s[i]-aver);}res=sqrt(res/m);ans=min(ans,res);return res;
}void simulate_anneal(){random_shuffle(a,a+n);//随机打乱现有序列for(double t=1e4;t>1e-4;t*=0.99){///模拟退火int p=random()%n;int q=random()%n;double lst=getans();//计算旧值swap(a[p],a[q]);double now=getans();//计算新值double delta=now-lst;if(exp(-delta/t)<(double)rand()/RAND_MAX){//以一定概率交换swap(a[p],a[q]);}}
}int main(){scanf("%d%d",&n,&m);for(int i=0;i<n;i++){scanf("%lf",&a[i]);}while((double)clock()/CLOCKS_PER_SEC<0.7){simulate_anneal();//卡时}printf("%.2lf\n",ans);return 0;
}