问题简述:
八皇后问题,一个古老而著名的问题,是回溯算法的典型案例。该问题由国际西洋棋棋手马克斯·贝瑟尔于 1848 年提出:在 8×8 格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
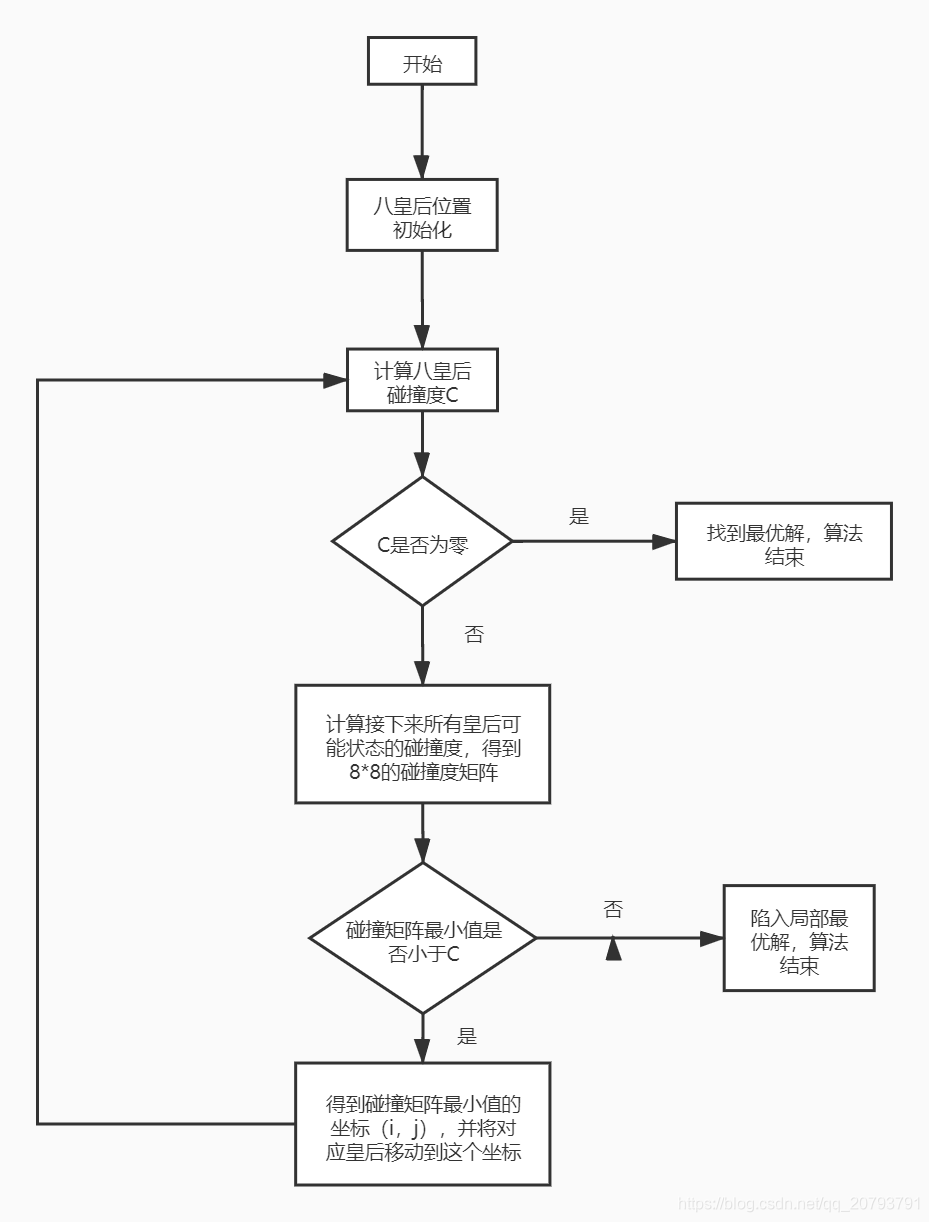
算法的逻辑流程图如下所示:
源代码为:
import copy import numpy as np import random import time# 爬山法解决八皇后问题# 八皇后初始化函数 def init():cache = {}m = np.zeros((8, 8), dtype=int)for i in range(0, 8):temp = random.randrange(0, 8)m[temp, i] = 1cache["queen" + str(i)] = [temp, i]return m, cache# 计算当前状态碰撞数量 def compute_weight_single(coord_cache):weight = 0for i in range(0, 8):x, y = coord_cache["queen" + str(i)]for j in range(i + 1, 8):_x, _y = coord_cache["queen" + str(j)]if _x - x == j - i or _x - x == i - j:weight += 1if _x == x:weight += 1return weight# 计算8X8的碰撞矩阵 def compute_weight_matrix(coord_cache):weight_matrix = np.zeros((8, 8))for i in range(0, 8):for j in range(0, 8):# fix bug# 此处需用dict.copy函数,直接写赋值会导致仅仅建立了一个引用,改变引用也会改变原来的值temp_coord_cache = coord_cache.copy()temp_coord_cache["queen" + str(i)] = [j, i]weight = compute_weight_single(temp_coord_cache)weight_matrix[j, i] = weightreturn weight_matrix# 根据碰撞矩阵调整皇后的位置 def next_move(cache, weight_matrix):coord_cache = cachemin = np.min(weight_matrix)for i in range(0, 8):for j in range(0, 8):if weight_matrix[j, i] == min:# 调整皇后的位置coord_cache["queen" + str(i)] = [j, i]return coord_cache# 把当前的皇后状态画出来 def draw(coord_cache):m = np.zeros((8, 8), dtype=int)for i in range(8):row, column = coord_cache["queen" + str(i)]row, column = int(row), int(column)m[row][column] = 1return m# 爬山算法 def climbing_algorithm():m, coord_cache = init()while True:weight = compute_weight_single(coord_cache) # 计算当前状态的碰撞值# print("当前的八皇后状态为:\n", draw(coord_cache))# print("当前的八皇后状态的碰撞度为\n", weight)if weight == 0: # 碰撞值为零,为目标状态,算法结束return Trueweight_matrix = compute_weight_matrix(coord_cache) # 计算8*8的碰撞矩阵# print("当前的碰撞矩阵为:\n", weight_matrix)# 如果碰撞矩阵的最小值都大于等于当前状态的碰撞值,则不能找到一个更好的解if weight_matrix.min() >= weight:return Falseelse:coord_cache = next_move(coord_cache, weight_matrix) # 移动皇后def climbing_algorithm_test(num):tic = time.time()success_case = 0fail_case = 0for i in range(num):if climbing_algorithm():print("第{0}个例子成功找到最优解".format(i))success_case += 1else:print("第{0}个例子失败".format(i))fail_case += 1toc = time.time()print("{0}个例子中成功解决的例子为:{1}".format(num, success_case))print("{0}个例子成功解决的百分比为:{1}".format(num, success_case / num))print("{0}个例子中失败的例子为:{1}".format(num, fail_case))print("{0}个例子失败的百分比为:{1}".format(num, fail_case / num))print("{0}个例子运行算法所需的时间为:{1}秒".format(num, toc - tic))climbing_algorithm_test(10000)
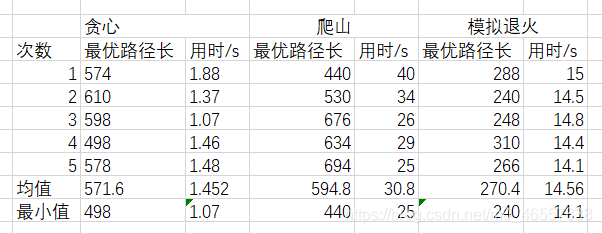
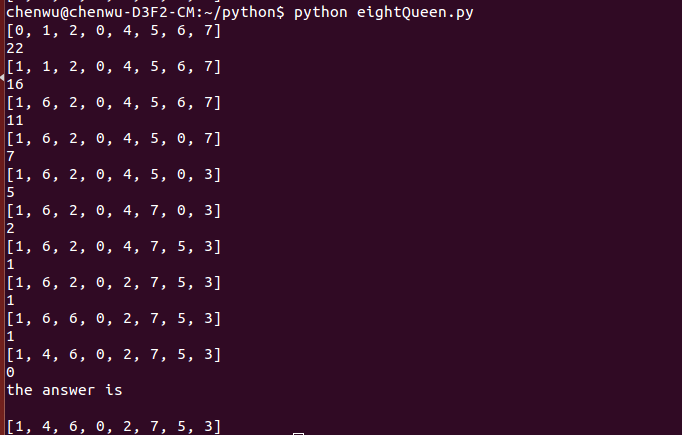
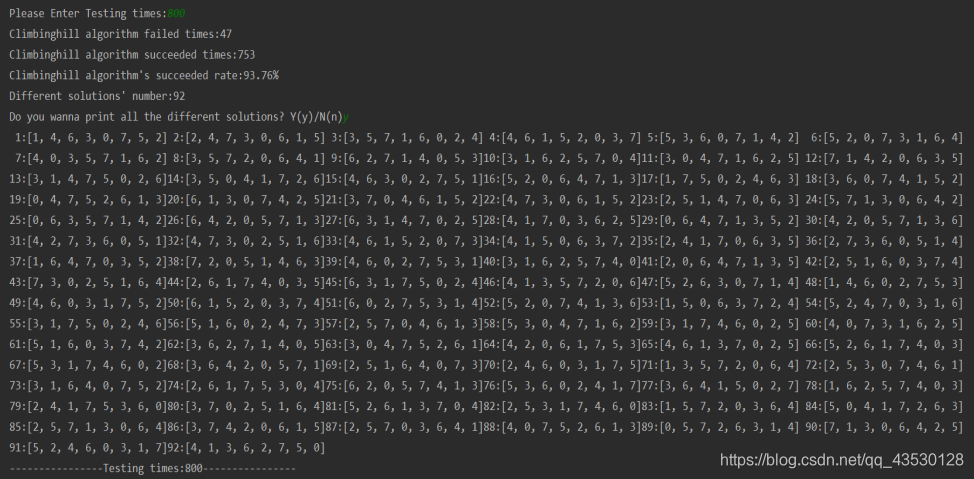
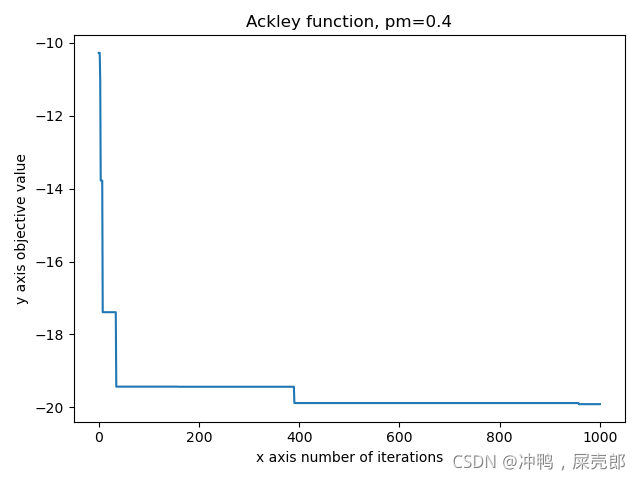
测试结果:
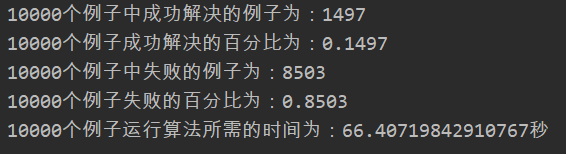
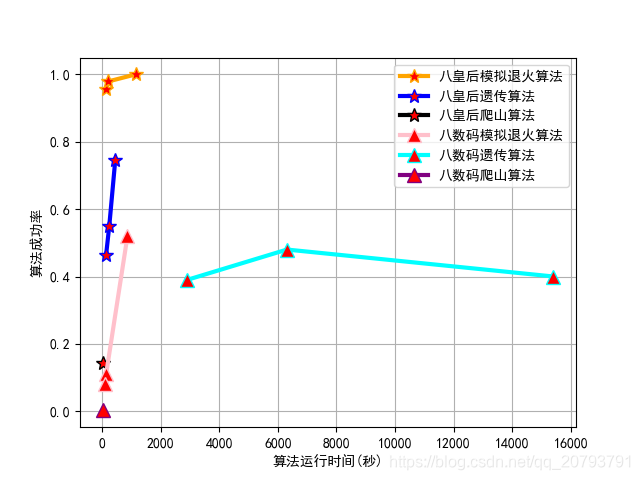
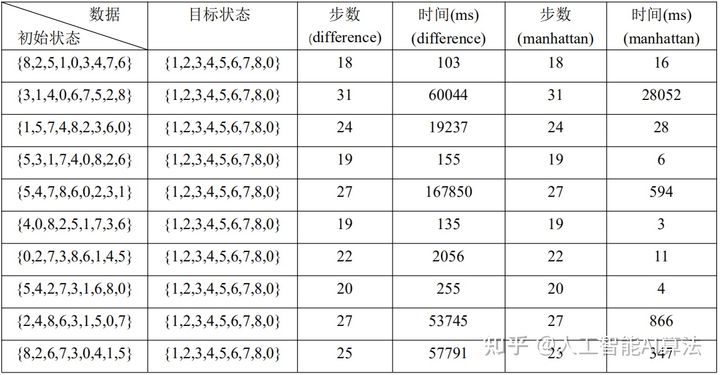
各算法解决八皇后八数码成功率: