问题描述：

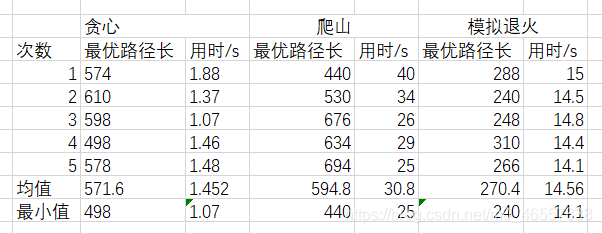
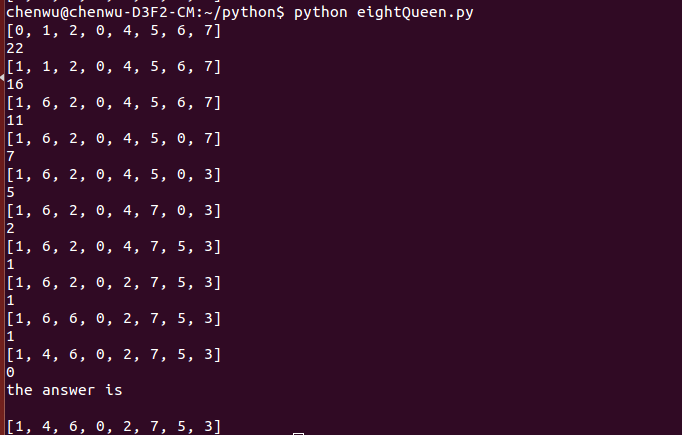
在一个3*3的方棋盘上放置着1,2,3,4,5,6,7,8八个数码,每个数码占一格,且有一个空格。这些数码可以在棋盘上移动，其移动规则是：与空格相邻的数码方格可以移入空格。现在的问题是：对于指定的初始棋局和目标棋局，给出数码的移动序列。该问题称八数码难题或者重排九宫问题。

 

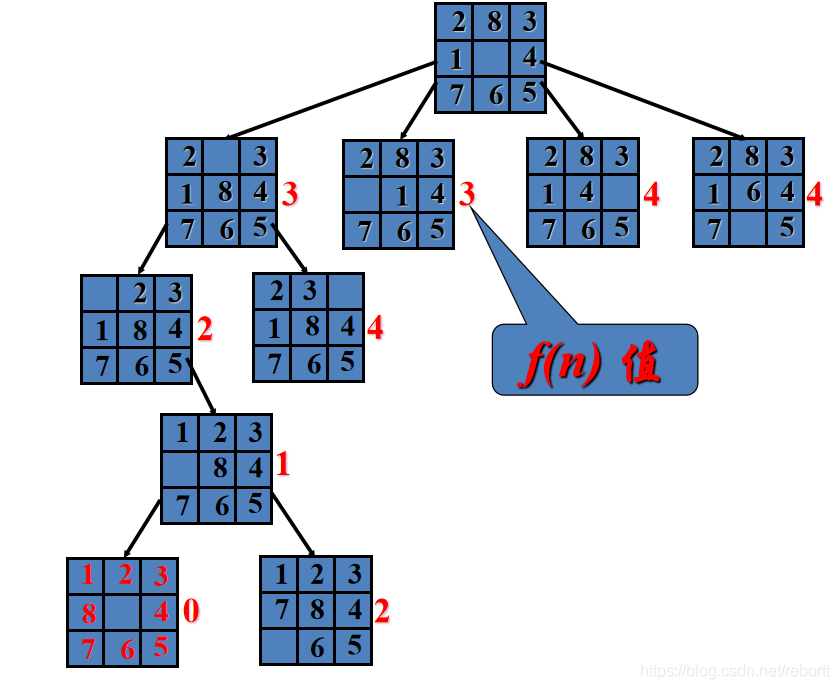
八数码问题的解决流程如下图所示：

 

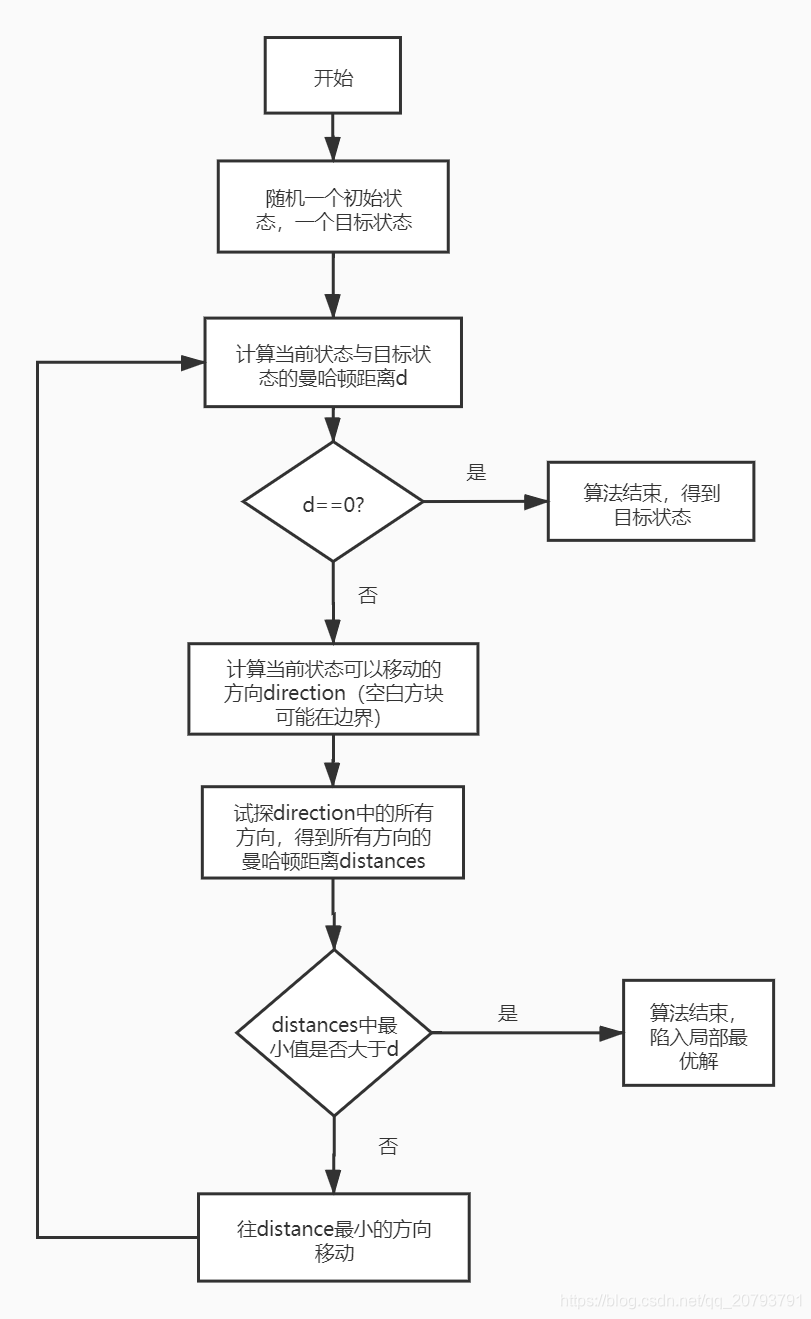
算法源代码为：

import copyimport numpy as np
import random
import time
import math# 爬山法解决八皇后问题
# 八数码初始化函数，返回一个初始状态和一个目标状态,这里0代表八数码中的空格
def init():init_state = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8])target_state = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8])np.random.shuffle(init_state)np.random.shuffle(target_state)init_state = np.reshape(init_state, (3, 3))target_state = np.reshape(target_state, (3, 3))return init_state, target_state# 计算当前状态和目标状态下的曼哈顿距离
def compute_manhattan_distance(init_state, target_state):total_distance = 0for i in range(1, 9):(init_row, init_column) = np.where(init_state == i)(target_row, target_column) = np.where(target_state == i)total_distance += abs(target_row - init_row) + abs(target_column - init_column)return int(total_distance)# 计算接下来所有可能的行动带来的曼哈顿距离
def compute_manhattan_distance_all(init_state, target_state):distances = {}coord_cache = {}# 获取空白方块的坐标zero_row, zero_column = np.where(init_state == 0)# 计算空白方块尝试往四个方向移动后产生状态的曼哈顿距离if zero_row - 1 >= 0:  # 如果空白方块在最上边则不能往上移，下面同理up_row, up_column = zero_row - 1, zero_columncoord_cache["up"] = [up_row, up_column]if zero_row + 1 <= 2:down_row, down_column = zero_row + 1, zero_columncoord_cache["down"] = [down_row, down_column]if zero_column - 1 >= 0:left_row, left_column = zero_row, zero_column - 1coord_cache["left"] = [left_row, left_column]if zero_column + 1 <= 2:right_row, right_column = zero_row, zero_column + 1coord_cache["right"] = [right_row, right_column]for i in coord_cache.keys():  # 移动到所有可以移动的方向，然后计算移动之后的曼哈顿距离以便接下来的贪心选择计算temp = init_state.copy()temp[zero_row, zero_column] = temp[coord_cache[i][0], coord_cache[i][1]]temp[coord_cache[i][0], coord_cache[i][1]] = 0distances[i] = compute_manhattan_distance(temp, target_state)return distances# 得到distances中曼哈顿距离最小的方向
def minimal_manhattan_distance(distances):temp = copy.deepcopy(distances)minimal_value = 1000for i in temp.keys():if distances[i] < minimal_value:minimal_value = distances[i]return minimal_value# 根据得到的曼哈顿距离进行下一步移动
def next_move(init_state, distances):current_state = init_state.copy()zero_row, zero_column = np.where(current_state == 0)# 获取移动的方向minimal_value = 1000key = ""for i in distances.keys():if distances[i] < minimal_value:minimal_value = distances[i]key = iif key == "up":  # 空格向上移动,下面同理print("向上移动")up_row, up_column = zero_row - 1, zero_columntemp = current_state[up_row, up_column]current_state[zero_row, zero_column] = tempcurrent_state[up_row, up_column] = 0if key == "down":print("向下移动")down_row, down_column = zero_row + 1, zero_columntemp = current_state[down_row, down_column]current_state[zero_row, zero_column] = tempcurrent_state[down_row, down_column] = 0if key == "left":print("向左移动")left_row, left_column = zero_row, zero_column - 1temp = current_state[left_row, left_column]current_state[zero_row, zero_column] = tempcurrent_state[left_row, left_column] = 0if key == "right":print("向右移动")right_row, right_column = zero_row, zero_column + 1temp = current_state[right_row, right_column]current_state[zero_row, zero_column] = tempcurrent_state[right_row, right_column] = 0return current_state# 爬山算法
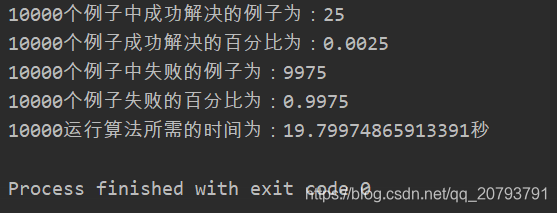
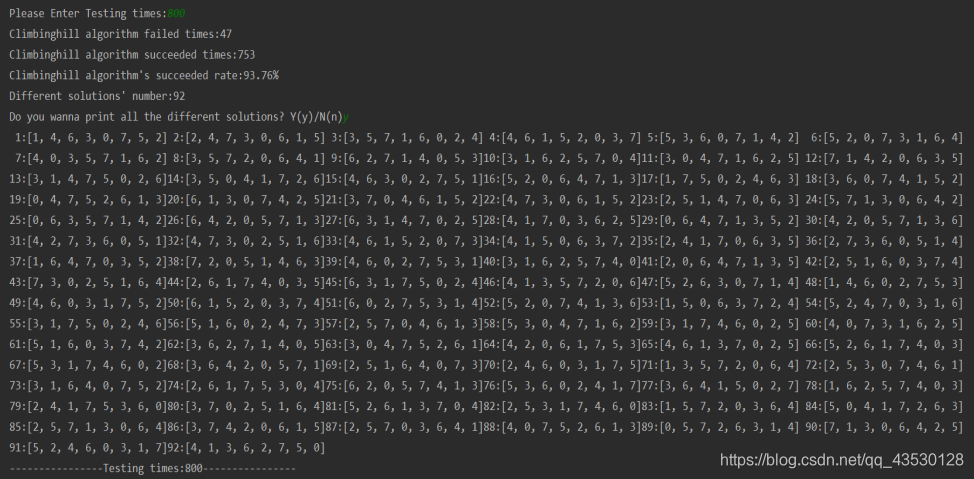
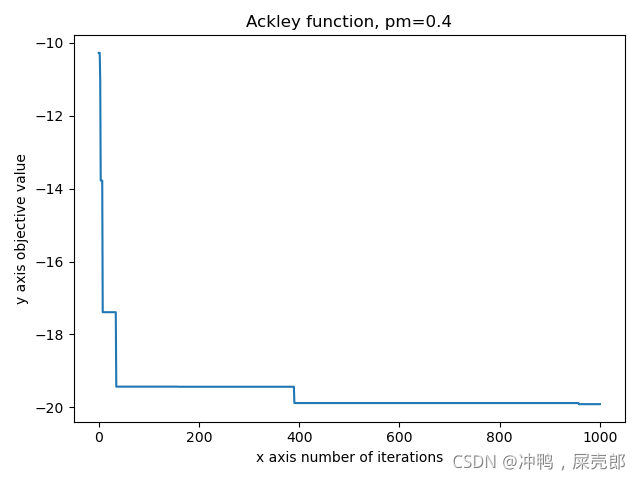
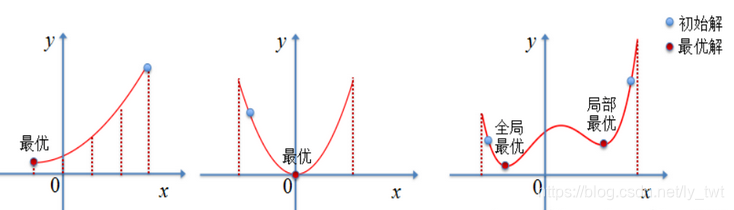
def climbing_algorithm():init_state, target_state = init()print("初始状态为：\n", init_state)print("目标状态为：\n", target_state)while True:current_manhattan_distance = compute_manhattan_distance(init_state, target_state)  # 计算当前状态与目标状态的曼哈顿距离print("当前状态距离目标的曼哈顿距离为：", current_manhattan_distance)if current_manhattan_distance == 0:  # 当前状态就是目标状态，算法结束return Truedistances = compute_manhattan_distance_all(init_state, target_state)  # 计算空白方块所有可以移动的方向和对应的曼哈顿值print("distances:", distances)print("distances里面的最小值为：", minimal_manhattan_distance(distances))if current_manhattan_distance <= minimal_manhattan_distance(distances):return False  # 即接下来无论如何移动的曼哈顿距离都大于目前的，则陷入了局部最优解init_state = next_move(init_state, distances)print("移动后的新状态为：\n", init_state)def climbing_algorithm_test(num):tic = time.time()success_case = 0fail_case = 0for i in range(num):print("第{0}个例子启动".format(i))if climbing_algorithm():success_case += 1print("第{0}个例子成功找到最优解".format(i))else:fail_case += 1print("第{0}个例子失败".format(i))toc = time.time()print("{0}个例子中成功解决的例子为：{1}".format(num, success_case))print("{0}个例子成功解决的百分比为：{1}".format(num, success_case / num))print("{0}个例子中失败的例子为：{1}".format(num, fail_case))print("{0}个例子失败的百分比为：{1}".format(num, fail_case / num))print("{0}运行算法所需的时间为：{1}秒".format(num, toc - tic))climbing_algorithm_test(10000)

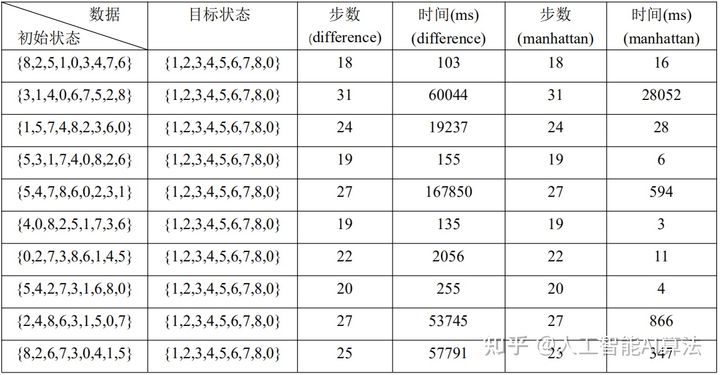
测试结果为：