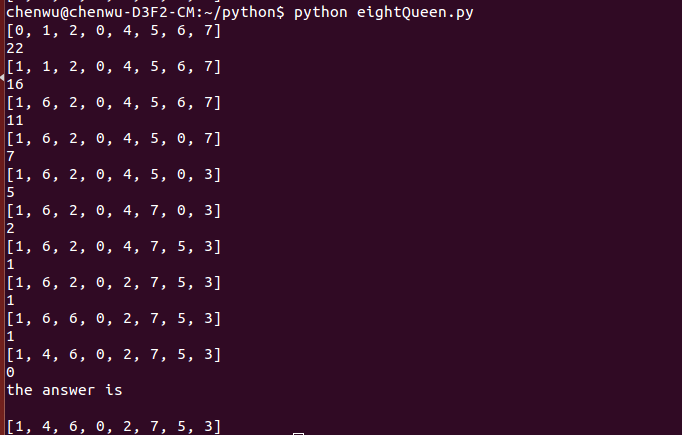
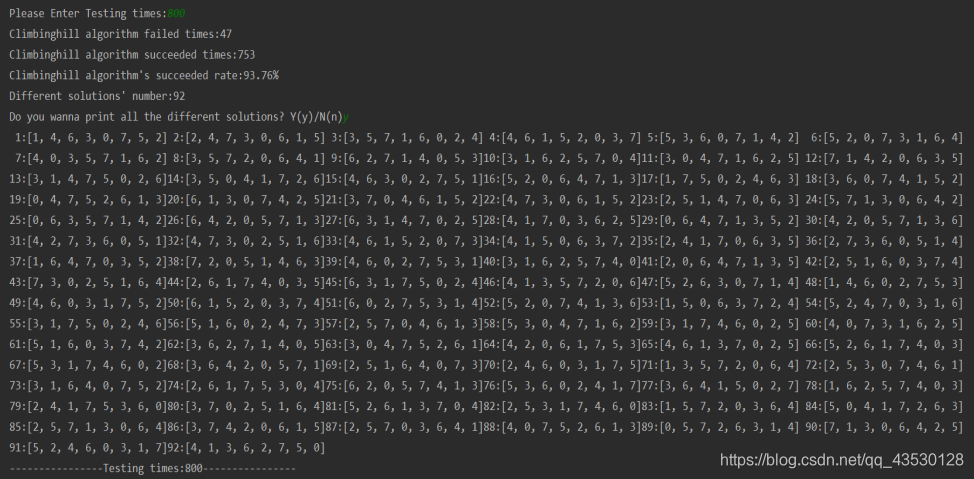
1.原理
爬山法(Hill Climbing)是一种局部搜索算法。局部搜索算法不关心求解目标的路径,只要求找到符合要求的解,通常对最优化问题十分有用。爬山法使用启发式函数(或代价评估函数)确定“标高”,找到目标的解就是要找到最高峰,即全局最大值。但是我们知道山外有山,山外还有一望无际的平原。爬山法存在局部最大值、山脊、高原等问题。爬山法经常被卡在某个局部最大值(或最小代价处),其成功率低到只有14%.解决此办法的通常思路是:使用随机爬山法(随机选择一个优于当前状态的状态)、首选爬山法(首先选择第一个优于当前状态的状态、对于上千后继比较管用)、随机重启爬山法(Random restart hill climbing,先随机生成一个初始状态,若不行再随机生成一个初始状态,直到找到目标)
N皇后问题的版本有:
(1)求解的个数
(2)求所有解(摆放方法)
(3)求一个解
其求解方法有:回溯法、递归法、深度优先搜索法等。甚至还有直接O(n)求解的算法,如https://blog.csdn.net/lyy289065406/article/details/78955101
本文以爬山法为例求解问题(3),权当一个例子。
2.数据结构
(1)皇后位置的表示
皇后有N个,需摆放在N*N的棋盘上,一种比较好的方法是用一个大小为N的数组来存放其位置。如:int s[N],第i行(或第一列)皇后存放的位置是s[i]
(2)冲突皇后的表示
一共有三条线:列冲突(生成初始状态时,每行一个、行不冲突)、主副对角线冲突(共2*N-1个),用三个数组表示:col[N]、pdiag[N]、cdiag[N]
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>#define SIZE 8
#define swap(a,b) {int t = a; a = b; b = t;}int s[SIZE]={0};
//int row[1000]={0};//row[i]表示第i行有几个皇后
int row[SIZE]={0};
int col[SIZE]={0};//col[i]表示第i列有几个皇后
//pdiag[i]表示第i根主对角线(principal diagonal)皇后个数(从左上到右下的线)
int pdiag[SIZE*2-1]={0};
//pdiag[i]表示第i根副对角线(counter diagonal)皇后个数(从右上到左下的线)
int cdiag[SIZE*2-1]={0};3.随机生成N个皇后、打印棋盘等
//打印棋盘
void print(int s[]){ printf("\n");for(int i=0;i<SIZE;i++) {for (int j = 0; j < SIZE; j++)if(s[i]==j) printf("● ");else printf("□ ");printf("\n");}}
//随机产生一个从start到end(不包括end)的数,x是随机因素
int myRandom(int start=0,int end=100,int x=0)
{srand((unsigned)time(NULL)+x);return rand()%(end-start);
}//随机生成皇后,这样生成的冲突值比较小,x可以生成不同的种子void randomQueen(int s[],unsigned x=0){for(int i=0;i<SIZE;i++)s[i]=myRandom(0,SIZE,i+x);}
4.启发式函数或代价评估函数
以相互冲突的皇后个数来评价状态的优劣。三条线:列线、主副对角线,皇后的冲突个数比较好计算。假设某条线上有n个皇后,则冲突个数为n*(n-1)*0.5。
int heuristic(int s[]){//重新对列、主、副对角线置0memset(row,0,sizeof(col)); memset(col,0,sizeof(col));memset(pdiag,0,sizeof(pdiag));memset(cdiag,0,sizeof(cdiag));int h=0;int s2=2*SIZE;for(int i=0;i<SIZE;i++) {col[s[i]]++;// row[i]++;//主(副)对角线条数是2*size,size为皇后总个数//主对角线编号:最右上角为0,最左下角为2*size-1//可以证明对角线上的下面p值都是一样,且为上面定义的编号 //int p=i - s[i] + SIZE - 1; pdiag[i - s[i] + SIZE - 1]++;//p为副对角线编号 //p=i+s[i];cdiag[i+s[i]]++; } for(int i=0;i<s2;i++){if(i<SIZE) {h+=(col[i]-1)*col[i]*0.5;//h+=(row[i]-1)*row[i]*0.5;}h+=pdiag[i]*(pdiag[i]-1)*0.5;h+=cdiag[i]*(cdiag[i]-1)*0.5;}return h;}5.调整某行皇后的列位置之前的代价评估
调整时只会影响调整前后的三条线上的冲突皇后个数,假设某类线上调整前的皇后个数分别为n1(从这里移除一个皇后)、n2(在该线上添加一个皇后),则调整后的个数分别为n1-1、n2+1,根据上面计算冲突皇后个数的公式,该类型线增加冲突个数为:
(n2+1-1)*(n2+1)*0.5-(n2-1)*n2*0.5-[(n1-1)*n1*0.5-(n1-1-1)*(n1-1)*0.5]
=0.5*n2*(n2+1-n2+1)-0.5*(n1-1)*(n1-n1+2)
=n2-n1+1
//将第row1行中的现有皇后调整到第col1列,然后计算其评估值
//h为现有评估值
int adjust(int s[],int row1,int col1,int h)
{//列上增加值 int nowCol=s[row1];//现在第row1行皇后所在列位置 h+=(col[col1]-col[nowCol]+1);//主对角线上增加值 h+=(pdiag[row1-col1+SIZE-1]-pdiag[row1-nowCol+SIZE-1]+1);//副对角线上增加值 h+=(cdiag[row1+col1]-cdiag[row1+nowCol]+1); return h;
}6.接受皇后的移动
应修改三条线上前后对应值、皇后位置
//接受第row1行的皇后移动到col1列
void accept(int s[],int row1,int col1)
{col[s[row1]]--;pdiag[row1-s[row1]+SIZE-1]--;cdiag[row1+s[row1]]--;s[row1]=col1;col[col1]++;pdiag[row1-col1+SIZE-1]++;cdiag[row1+col1]++;
}7.当评估代价为1时尝试手工修改位置
该函数效果是有,但不那么明显。评估代价为1时一定有1对皇后冲突,具体来讲一定是某列上有2个皇后、某列上没有皇后。找出这两列,然后在皇后位置数组找到对应行,尝试将有2个皇后的列的其中一个皇后调整到没有皇后的列。
int findTwo(int s[])
{int col0,col2,flag=0;int row0,row2;for(int i=0;i<SIZE;i++){//为0表示某列没有皇后 if(col[i]==0) {col0=i;flag++;}//为2表示某列有2个皇后 if(col[i]==2) {col2=i;flag++;}if(flag==2) break;}flag=0; for(int i=0;i<SIZE;i++)if(s[i]==col2) {flag++;//试着将2个皇后的其中一个皇后调整到没有皇后的列(col0) //将其临时调整到第i行,col0列,如果对角线有1个皇后显然不行 if(pdiag[i-col0+SIZE-1]==0 && cdiag[i+col0]==0){s[i]=col0;printf("\n成功!\n");return 1;}if(flag==2) return 0;} return 0;
}8.随机对调4行皇后位置
经过尝试,随机对调一对皇后的位置用处不大,调整2对皇后的位置效果很明显。调整的2行应不是同一行。
void exchange(int s[],int c)
{int r1,r2,r3,r4,k1=0,k2=1;do{srand((unsigned)time(NULL)+k1);r1=rand()%(SIZE);r2=rand()%(SIZE);k1++;}while(r1==r2);swap(s[r1],r2);do{srand((unsigned)time(NULL)+c+k2);r3=rand()%(SIZE);r4=rand()%(SIZE);k2++;}while(r3==r4);swap(s[r3],r4);
}9.爬山法函数的实现
采取首选爬山法,一旦发现有更优状态,立即执行动作进入该后继状态。其效果相比其他要好些。另外还使用了一个技巧,当到达局部山峰后,采用随机交换4行皇后位置(2行不足以平稳过渡、超过4行后面的代价可能较大),来度过该山峰。
int hillClimbing(int s[]){int h=heuristic(s);int curr=h;//当前评估代价int min=h;//最小代价int lastMin=h;//上一轮最小代价//下面这几个都是计数器//int counter=0;//最初想随机选择一个优于当前的状态的后继int c=0;//迭代轮次int cc=0;//交换次数int k=0;//没大用while (1){//counter=0;c++;int flag=0;int minValue=s[0],minLine=0;//分别为:代价最小时的皇后的列号、行号for(int i=0;i<SIZE;i++) //第i行 {for(int j=0;j<SIZE;j++)//第i行皇后放第j列上 {if(j!=s[i]) //s[i]为第i行皇后的列号 {//临时调整:将第i行的皇后放在第j列上,计算评估值 h=adjust(s,i,j,curr);//counter++;if(h<=min){minLine=i;minValue=j;accept(s,i,j);min=h;} if(h==0 || h==1) //特殊处理{flag=1;break;}}} if(flag==1) break;}//printf("%d ",min);if(min==0) //代价为0,表示已找到一种N皇后的排列{ printf("\n迭代次数:%d\n",c);printf("\n随机交换次数:%d\n",cc); s[minLine]=minValue;return c;}else if(min==1) //用findTwo函数手工调整{accept(s,minLine,minValue); if(findTwo(s)) {printf("\n迭代次数:%d\n",c);printf("\n随机交换次数:%d\n",cc); return c;}else //调整失败,还是用随机交换大法,管用{cc++;exchange(s,c);curr=heuristic(s);lastMin=curr;min=curr;}}else if(min==lastMin) //到达局部山峰,无法前进,只好随机交换大法{s[minLine]=minValue;if(k==1) //计数器{cc++;exchange(s,c);curr=heuristic(s);lastMin=curr;min=curr;k=0; }k++;}else{accept(s,minLine,minValue);curr=min;lastMin=min;} }}10.测试及结果
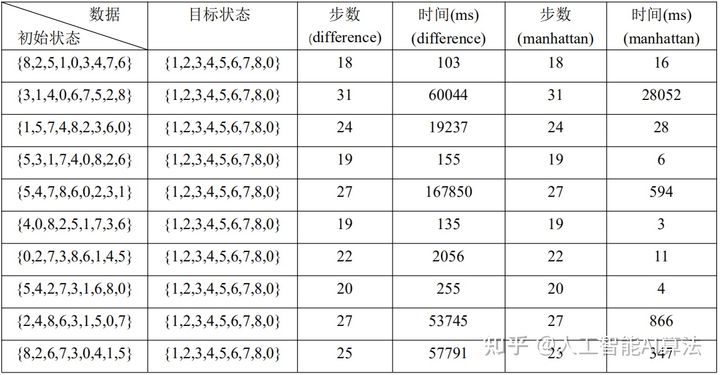
//最前面有个符号常量SIZE表示皇后的个数,可修改它,看不同皇后个数花费的时间int main(int argc,char *argv[]) {//int s[SIZE]={4,5,6,3,4,5,6,5};//int s[SIZE]={2,0,6,3,1,4,7,5};randomQueen(s,SIZE);printf("开始大小:%d\n",heuristic(s));printf("\n次数:%d\n",hillClimbing(s));printf("结束大小:%d\n",heuristic(s)); return 0; }| 皇后个数 | 初始冲突个数 | 花费时间 | 迭代次数 | 随机交换次数 |
| 8 | 5 | 0.24s | 12 | 4 |
| 100 | 49 | 0.26s | 42 | 18 |
| 500 | 337 | 0.46s | 13 | 4 |
| 1000 | 351 | 3.7s | 239 | 101 |
| 2000 | 1341 | 13.05s | 230 | 100 |
| 3000 | 1325 | 170.4 | 1321 | 544 |
| 5000 | 6463 | 907.7 | 2542 | 1023 |
11.结论与问题
爬山法的确能快速找到一个结果,但是其成功率比较低,需要借助随机大法:随机选择较好的后继状态、随机交换、随机重启等。经过测试首选爬山法效果的确优于其他方法,因为它每次都更接近目标状态,而其他方法则是每轮才更接近目标状态。
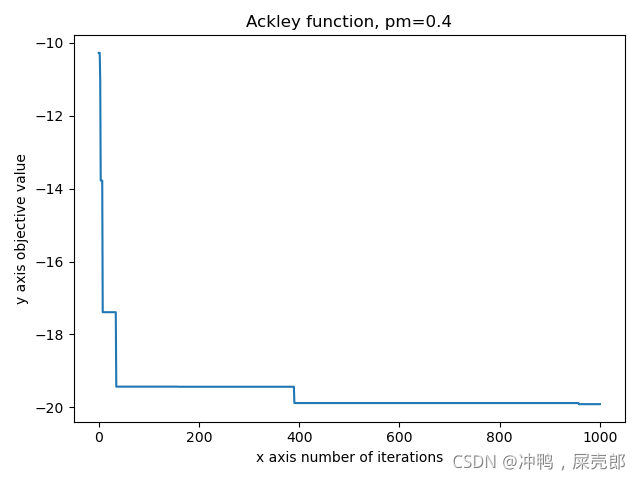
另一个问题是,当爬山法基本要靠近目标状态时,却遇到了山峰,无法更近一步了,如N皇后问题,总是在冲突数10以下循环(如下图),导致消耗一定时间(如上表,随机交换次数太多)。

除此之外,有时受制于初始状态,有可能皇后个数多一倍,但其所花费时间却少很多的现象,当然还有另一个极端,这些可以进行多次测试取平均值。当皇后个数超过5000时,所花费时间就较多了,时间关系没有测试。
《人工智能-一种现代的方法》一书中,说300万个的皇后问题一分钟就能找到解,这是怎么做到的????
目前,找了一下比较好的10000个皇后1s不到(https://blog.csdn.net/CristianoJason/article/details/50964675),但发现30000个皇后也要好几秒,上100000后就很慢了。所以300万个1分钟怎么做的?