文章目录
- 1 八皇后问题
- 2 程序代码
- 2.1 程序1
- 2.2 程序2
- 2.3 程序3
- 2.3.1 爬山法
- 2.3.2 随机重启爬山法
- 2.3.3 允许皇后侧移的爬山法
- 3 评价
1 八皇后问题
有一个8乘8的棋盘,现在要将八个皇后放到棋盘上,满足:对于每一个皇后,在自己所在的行、列、两个对角线都没有其他皇后。

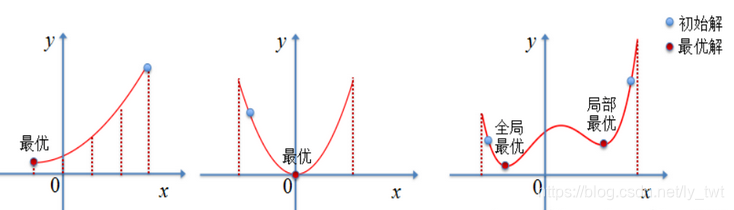
不了解爬山法、随机重启爬山法、允许侧移的爬山法的话,请看这里。
规定棋盘的同列只能出现一个皇后。每一个棋盘,对应于一个长度为8的序列,每一个数的范围是[1, 8],第k个数字所代表的含义是第k列中皇后所在的行数,如[3,2,5,4,3,2,1,3]代表棋盘上从第一列到第八列,皇后所摆放的行数分别为第3,2,5,4,3,2,1,3行。任意状态(包括初始状态)的所有后继状态为【从当前状态开始,将任意一个皇后移到同列的其他7个格子后的所有状态】。对于任意一个已有八个皇后的棋盘(当然同一列有且仅有一个皇后)的后继状态均有8*7=56个。
2 程序代码
2.1 程序1
程序1:generate_init_seq.py。如果8个皇后在8*8的棋盘上可以随意摆放,当然是不能在同一个格子里放超过一个皇后的情况下,本来所有需要测试是否满足要求的序列共有64*63*…*57=1.78e+14个,这太多了。所以此程序的工作是筛选出那些【每行与每列都只有一个皇后存在】的序列,这样的序列有8*7*6*5*4*3*2=40320个,可以大大缩减后续程序的运行时间,而且这样在后面处理每个序列时只需要考虑两条对角线上和所在的行上有没有其他皇后即可(不用考虑列)。如下:
import json
import timestart = time.time()seq = [[i, j, k, l, m, n, o, p]for i in range(1, 9)for j in range(1, 9)for k in range(1, 9)for l in range(1, 9)for m in range(1, 9)for n in range(1, 9)for o in range(1, 9)for p in range(1, 9)if all([i != j, i != k, i != l, i != m, i != n, i != o, i != p,j != k, j != l, j != m, j != n, j != o, j != p,k != l, k != m, k != n, k != o, k != p,l != m, l != n, l != o, l != p,m != n, m != o, m != p,n != o, n != p,o != p])] # 筛选出【每行与每列都只有一个皇后】的序列print('有' + str(len(seq)) + '个可能的序列')with open('seq.json', 'w') as file_object:json.dump(seq, file_object)end = time.time()print('Successful!')
print('已将生成的序列存储到文件seq.json中,用时' + str('%.2f' % (end - start)) + 's')
输出如下。注意会生成一个文件seq.json,我上传到了csdn上,你可以看看这里,你也可以运行程序1,就可以在自己电脑上得到一个文件,除了运行时间有区别,其他输出和我这个是一样的:
有40320个可能的序列
Successful!
已将生成的序列存储到文件seq.json中,用时17.61s
2.2 程序2
程序2:functions.py。包括两个函数:attacked_queens_pairs, display_board,分别完成【计算序列对应棋盘的互相攻击的皇后对数】和【打印输出序列对应的棋盘】的功能。如下:
import numpy as npdef attacked_queens_pairs(seqs):"""计算序列对应棋盘的【互相攻击的皇后对数n】,0<=n<=28,最优解要满足n=0只需要检查当前棋盘的八个皇后在各自的行和两条对角线上是否有其他皇后,不需判断同列是否有其他皇后"""a = np.array([0] * 81) # 创建一个有81个0的一维数组a = a.reshape(9, 9) # 改为9*9二维数组。为方便后面使用,只用后八行和后八列的8*8部分,作为一个空白棋盘n = 0 # 互相攻击的皇后对数初始化为0for i in range(1, 9):a[seqs[i - 1]][i] = 1 # 根据序列,按从第一列到最后一列的顺序,在空白棋盘对应位置放一个皇后,生成当前序列对应的棋盘for i in range(1, 9):for k in list(range(1, i)) + list(range(i + 1, 9)): # 检查每个皇后各自所在的行上是否有其他皇后if a[seqs[i - 1]][k] == 1: # 有其他皇后n += 1t1 = t2 = seqs[i - 1]for j in range(i - 1, 0, -1): # 看左半段的两条对角线if t1 != 1:t1 -= 1if a[t1][j] == 1:n += 1 # 正对角线左半段上还有其他皇后if t2 != 8:t2 += 1if a[t2][j] == 1:n += 1 # 次对角线左半段上还有其他皇后t1 = t2 = seqs[i - 1]for j in range(i + 1, 9): # 看右半段的两条对角线if t1 != 1:t1 -= 1if a[t1][j] == 1:n += 1 # 正对角线右半段上还有其他皇后if t2 != 8:t2 += 1if a[t2][j] == 1:n += 1 # 次对角线右半段上还有其他皇后return int(n/2) # 返回n/2,因为A攻击B也意味着B攻击A,因此返回n的一半def display_board(seqs):"""显示序列对应的棋盘"""board = np.array([0] * 81) # 创建一个有81个0的一维数组board = board.reshape(9, 9) # 改变为9*9二维数组,为了后面方便使用,只用后八行和后八列的8*8部分,作为一个空白棋盘for i in range(1, 9):board[seqs[i - 1]][i] = 1 # 根据序列,从第一列到最后一列的顺序,在对应位置放一个皇后,生成当前序列对应的棋盘print('对应棋盘如下:')for i in board[1:]:for j in i[1:]:print(j, ' ', end="") # 有了end="",print就不会换行print() # 输出完一行后再换行,这里不能是print('\n'),否则会换两行
此程序无任何输出,只是定义了2个函数以供主程序调用。
2.3 程序3
2.3.1 爬山法
程序3:main.py。为主程序,通过调用程序2的两个函数,完成爬山法解决八皇后问题的全过程。如下:
import json
import random
from functions import attacked_queens_pairs, display_boardwith open('seq.json', 'r') as file_object:seqs = json.load(file_object) # 载入保存好的序列current_seqs = random.choice(seqs) # 随机挑选一个序列print('随机挑选的初始序列为:' + str(current_seqs))
display_board(current_seqs)while True:successors = [] # 当前状态的后继状态集合count = 0 # 计数变量dicts = [] # 由一个个字典组成的列表,每个字典有两项内容:序列及对应棋盘互相攻击皇后对数a = list(range(1,9))for item in current_seqs:for i in a[:item - 1] + a[item:]:seqs_tmp = list(current_seqs)seqs_tmp[count] = isuccessors.append(seqs_tmp) # 生成当前棋盘的后继状态,任意棋盘对应的后继状态都有56种count = count + 1if count == 8:breakfor s in successors:tmp_pair = attacked_queens_pairs(s)dicts.append({'seqs':s, 'attacked_queens_pairs':tmp_pair})nums = []for d in dicts:nums.append(d['attacked_queens_pairs']) # 获取所有后继状态的攻击的皇后对数,共56个值mins = min(nums) #取最小的current_attacked_queens_pairs = attacked_queens_pairs(current_seqs)if mins >= current_attacked_queens_pairs: # 当前棋盘最好answer = current_seqs # 算法最终运算结果为当前棋盘breaktemp = []for d in dicts:if d['attacked_queens_pairs'] == mins:temp.append(d['seqs']) # 存储互相攻击的皇后对数最少的棋盘,因为可能不止一个,因此用列表存储current_seqs = random.choice(temp) # 随机选择一个棋盘作为当前棋盘print('------') # 执行这条语句意味着爬山法结束了
if attacked_queens_pairs(answer) == 0:print('已找到最优解序列:' + str(answer))display_board(answer)
else:print('本次搜索未找到最优解,最好的序列为:' + str(answer))print('攻击的皇后对数为'+ str(attacked_queens_pairs(answer)))display_board(answer)
一种输出如下:
随机挑选的初始序列为:[8, 3, 2, 7, 6, 4, 5, 1]
对应棋盘如下:
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
------
已找到最优解序列:[3, 6, 2, 7, 1, 4, 8, 5]
对应棋盘如下:
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 0 1 0
另一种输出如下:
随机挑选的初始序列为:[2, 1, 6, 8, 5, 3, 4, 7]
对应棋盘如下:
0 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
------
本次搜索未找到最优解,最好的序列为:[3, 1, 6, 8, 5, 2, 4, 7]
攻击的皇后对数为1
对应棋盘如下:
0 1 0 0 0 0 0 0
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
上面列出了两种输出,第一种找到了最优解,第二种找到的是局部最优解。
通常爬山法可以以很快的速度找到问题的解,因为一般从较差的状态开始扩展是很容易做到的。但是爬山法经常也会陷入局部最优而难以“自拔”,也就是说在算法执行过程中有可能到达这样一种状态——在这个状态下再也做不到更好的改善了。如在解决八皇后问题中,首先从随机生成的一个上面有八个皇后的棋盘开始,使用最陡峭上升的爬山法(steepest-ascent hill climbing)在86%的情况下会陷入局部最优,且仅能在14%的情况下解决问题。爬山法过程比较快,在解决八皇后问题中,平均下来只需四步便可成功得到解,但是同样地,在可能在第三步就陷入了局部最优。下面改变策略,使用随机重启爬山法改进算法。
2.3.2 随机重启爬山法
随机重启爬山法的思想:如果一开始没有成功,那就再试一次,若还没成功就继续尝试。
程序3:main.py。为主程序。如下:
import json
import random
from functions import attacked_queens_pairs, display_boardwith open('seq.json', 'r') as file_object:seqs = json.load(file_object) # 载入保存好的序列current_seqs = random.choice(seqs) # 随机挑选一个序列print('随机挑选的初始序列为:' + str(current_seqs))
display_board(current_seqs)while True:successors = [] # 当前状态的后继状态集合count = 0 # 计数变量dicts = [] # 由一个个字典组成的列表,每个字典有两项内容:序列及对应棋盘互相攻击皇后对数a = list(range(1,9))for item in current_seqs:for i in a[:item - 1] + a[item:]:seqs_tmp = list(current_seqs)seqs_tmp[count] = isuccessors.append(seqs_tmp) # 生成当前棋盘的后继状态,任意棋盘对应的后继状态都有56种count = count + 1if count == 8:breakfor s in successors:tmp_pair = attacked_queens_pairs(s)dicts.append({'seqs':s, 'attacked_queens_pairs':tmp_pair})nums = []for d in dicts:nums.append(d['attacked_queens_pairs']) # 获取所有后继状态的攻击的皇后对数,共56个值mins = min(nums) #取最小的current_attacked_queens_pairs = attacked_queens_pairs(current_seqs)if mins < current_attacked_queens_pairs: # 后继状态更好temp = []for d in dicts:if d['attacked_queens_pairs'] == mins:temp.append(d['seqs']) # 存储互相攻击的皇后对数最少的棋盘,因为可能不止一个,因此用列表存储current_seqs = random.choice(temp) # 随机选择一个棋盘作为当前棋盘elif current_attacked_queens_pairs != 0: # 当前状态不是最优解current_seqs = random.choice(seqs) # 从初始序列集随机重新挑选一个序列else:answer = current_seqs # 当前状态为最优解breakprint('------') # 执行这条语句意味着爬山法结束了
print('已找到最优解序列:' + str(answer))
print('互相攻击的皇后对数为' + str(attacked_queens_pairs(answer)))
display_board(answer)
一种输出如下:
随机挑选的初始序列为:[7, 1, 8, 6, 3, 2, 4, 5]
对应棋盘如下:
0 1 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0
------
已找到最优解序列:[6, 3, 7, 2, 8, 5, 1, 4]
互相攻击的皇后对数为0
对应棋盘如下:
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0
算法从随机产生的初始状态开始,执行一系列的爬山搜索过程,若没找到最优解,就再生成一个初始状态,进行搜索,直到找到目标时算法才停止。随机重启爬山法完备的概率接近于1,即随机重启爬山法大多都可以找到解。
2.3.3 允许皇后侧移的爬山法
程序3:main.py。为主程序,通过调用程序2的两个函数,完成允许皇后侧移的爬山法解决八皇后问题的全过程。如下:
import json
import random
from functions import attacked_queens_pairs, display_boardwith open('seq.json', 'r') as file_object:seqs = json.load(file_object) # 载入保存好的序列current_seqs = random.choice(seqs) # 随机挑选一个序列print('随机挑选的初始序列为:' + str(current_seqs))
display_board(current_seqs)while True:successors = [] # 当前状态的后继状态集合count = 0 # 计数变量dicts = [] # 由一个个字典组成的列表,每个字典有两项内容:序列及对应棋盘互相攻击皇后对数a = list(range(1,9))for item in current_seqs:for i in a[:item - 1] + a[item:]:seqs_tmp = list(current_seqs)seqs_tmp[count] = isuccessors.append(seqs_tmp) # 生成当前棋盘的后继状态,任意棋盘对应的后继状态都有56种count = count + 1if count == 8:breakfor s in successors:tmp_pair = attacked_queens_pairs(s)dicts.append({'seqs':s, 'attacked_queens_pairs':tmp_pair})nums = []for d in dicts:nums.append(d['attacked_queens_pairs']) # 获取所有后继状态的攻击的皇后对数,共56个值mins = min(nums) #取最小的current_attacked_queens_pairs = attacked_queens_pairs(current_seqs)if mins < current_attacked_queens_pairs: # 后继状态更好temp = []for d in dicts:if d['attacked_queens_pairs'] == mins:temp.append(d['seqs']) # 存储互相攻击的皇后对数最少的棋盘,因为可能不止一个,因此用列表存储current_seqs = random.choice(temp) # 随机选择一个棋盘作为当前棋盘elif current_attacked_queens_pairs != 0: # 当前状态不是最优解a = list(range(8))pos1 = random.choice(a)a.remove(pos1)pos2 = random.choice(a)current_seqs[pos1],current_seqs[pos2] = current_seqs[pos2],current_seqs[pos1]else:answer = current_seqs # 当前状态为最优解breakprint('------') # 执行这条语句意味着爬山法结束了
print('已找到最优解序列:' + str(answer))
print('互相攻击的皇后对数为' + str(attacked_queens_pairs(answer)))
display_board(answer)
输出如下:
随机挑选的初始序列为:[2, 7, 6, 8, 4, 5, 3, 1]
对应棋盘如下:
0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
------
已找到最优解序列:[2, 4, 6, 8, 3, 1, 7, 5]
互相攻击的皇后对数为0
对应棋盘如下:
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
在上述爬山法代码中,若到达了局部最优状态时,允许任意一对(并且只允许一对)皇后横向移动,例如将第2列和第7列的皇后移入对方行的位置。这种改进方案可以大大提高爬山法解决八皇后问题的成功概率,上述代码基本上每次运行都可以得到解序列。
3 评价
自己需要补充模拟退火算法的代码
END