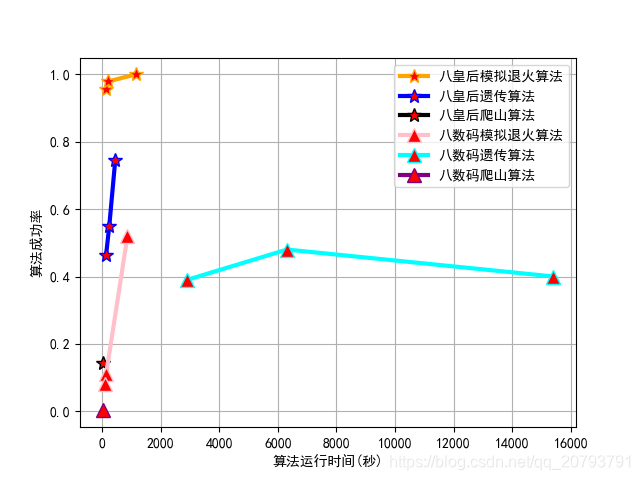
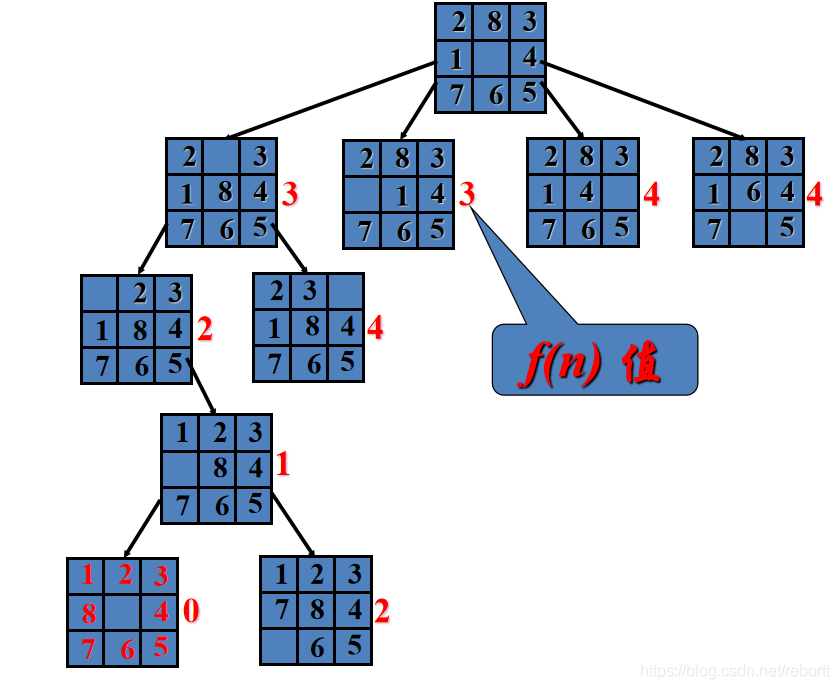
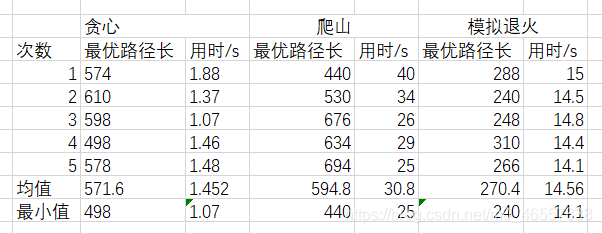
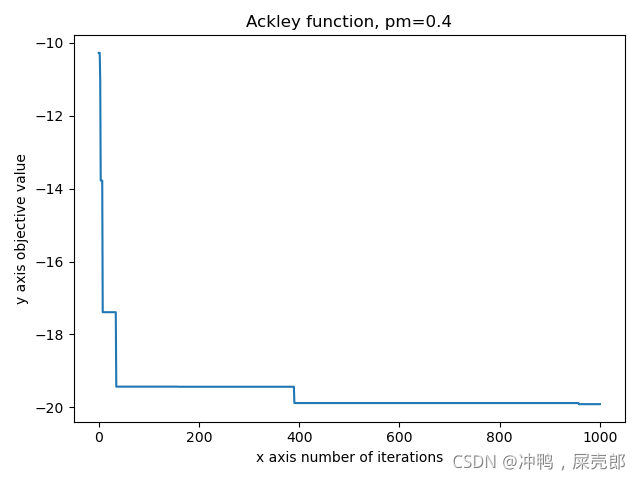
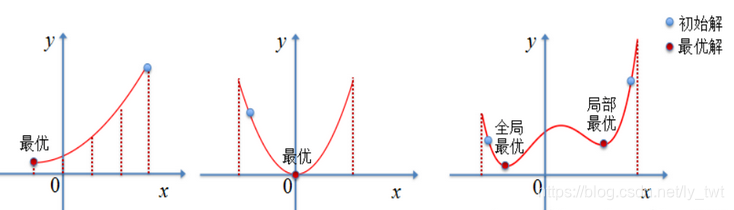
以下均假设最优解是在最低点。

爬山法

爬山算法是一种局部择优的方法，采用启发式方法，是对深度优先搜索的一种改进，它利用反馈信息帮助生成解的决策。

直白地讲，就是当目前无法直接到达最优解，但是可以判断两个解哪个更优的时候，根据一些反馈信息生成一个新的可能解。

因此，爬山算法每次在当前找到的最优方案 $x$ 附近寻找一个新方案。如果这个新的解 $x^{\prime }$ 更优，那么转移到 $x^{\prime }$，否则不变。

这种算法对于单峰函数显然可行。

Q：既然都知道是单峰函数了为什么不三分呢?

A：你说的对！直接三分好了。

B：我要是知道是单峰函数，我还在这里骗分？？？

爬山算法会引入『温度参数』 $T$。

类比的说，爬山就是一个醉汉喝得狂醉然后再山上裸奔蹦迪。

他知道该回家了（不然就要跪搓衣板），然后每次会往他认为最低的地方狂奔过去（中途不刹车）。

显然他可能一次恰好奔到山脚然后下山回家，也有可能奔过了到另一座山顶上去了。

不过没关系，醉汉奔过头了还会存在奔回来的可能。

但显然这个过程很没用。仿佛醉汉回家全靠天公作美。

所以在暴走过程中，他会经受山顶寒风的摧残，酒精作用渐渐消减，他变得越发清晰。

他就变得谨慎一点，每次少奔一点以达到山脚最低点位置。

这就要引入『降温参数』来起到缓缓冷静的作用。

关于『降温参数』，一般是 $[0.985,0.999]$ 中选，这样才能做到慢慢消减。

显然如果存在多个”转折“时，爬山就很容易进入局部最优解，而非全局最优解。

随着头脑逐渐清醒，醉汉蹦出局部最优解的期望就会更小，很有可能一直跳不过去某个坡。

模拟退火

为什么会有上面情况的产生呢？

其实是因为爬山法的写法，只有在新解优于当前解的时候，我们才会接受新解并移动到相应位置。

根据这种情况，我们知道其实偶尔新解不好我们也要去接受，这样才会存在跳出这个坡的可能。

这就是模拟退火了。

模拟退火相较于爬山就只是多了一个随机接受非最优解的部分，大大增加了找到全局最优解得可能。

以下是追根溯源，由物理和化学知识迁移到信息学上应用：

我们知道在分子和原子的世界中，能量越大，意味着分子和原子越不稳定，当能量越低时，原子越稳定。

『退火』是物理学术语，指对物体加温在冷却的过程。

模拟退火算法来源于晶体冷却的过程，如果固体不处于最低能量状态，给固体加热再冷却，随着温度缓慢下降，固体中的原子按照一定形状排列，形成高密度、低能量的有规则晶体（即全局最优解）。

而如果温度下降过快，可能导致原子缺少足够的时间排列成晶体的结构，结果产生了具有较高能量的非晶体（即局部最优解）。

因此就可以根据退火的过程，给其再增加一点能量，然后再冷却，如果增加能量，跳出了局部最优解，那么本次退火就是成功的。

模拟退火由两个部分组成：$\text{Metropolis}$ 算法和退火过程。

$\text{Metropolis}$ 算法就是如何在局部最优解的情况下让其跳出来，是退火的基础。

$\text{Metropolis}$ 提出的以概率来接受新状态的重要性采样方法，而非使用完全确定的规则，称为$\text{Metropolis}$ 准则，计算量较低。

假设我们从 $A$ 开始求解。先跳到 $B$，然后发现 $B$ 更优，绝对接受。$B$ 又跳到 $C$，绝对接受。$C$ 跳到 $D$ ，哎呀更差了呢！此时我们以一定的概率选择是否接受；假设接受，$D$ 又跳到 $E$ 发现比之前跳到的所有位置都优，直接接受，$E$ 继续跳$\dots \dots$ ；不接受，就还停在 $C$ 又开始随机下一个解。

至于这个接受概率是多少呢？已经有前人计算出来了。$x:$ 当前最优解，$x^{\prime }:$ 产生的新解
$$P=\{\begin{array}{l}1E(x^{\prime })<E(x)\\ e^{-\frac{E(x^{\prime })-E(x)}{T}}E(x^{\prime })\ge E(x)\end{array}$$
从这个式子我们可以看出，如果新解更优，那么百分之百绝对接受；否则我们会以 $P$ 的概率接受。

$\text{Metropolis}$ 算法虽然说是模拟退火算法的基础，但直接使用的话可能导致寻找解得速度太慢，以至于无法过题。

为了确保在有限的时间收敛，必须设定控制算法收敛的参数。

在上面的公式中，可以调节的参数就是『温度参数』$T$。

• $T$ 如果过大，就会导致退火太快，迭代次数不够，最后停留在局部最优值就会结束迭代。
• $T$ 如果较小，则计算时间会增加。

实际应用中采用退火温度表，在退火初期采用较大的 $T$ 值，随着退火的进行，逐步降低：

• 初始的温度 $T_0$ 应选的足够高，使的所有转移状态都被接受。初始温度越高，获得高质量的解的概率越大，但耗费的时间也越长。

• 退火速率。

  • 指数式下降：$T_n=\lambda T_n,n=1,2,3,...$。$\lambda$ 即是爬山算法里面的『降温参数』，选取的值同样遵守 $<1$ 又逼近 $1$ 原则。

    这种方式最常见，且对每一温度，有足够的转移尝试，但其收敛速度比较慢。

  • 其它方式：

    • $T_n=\frac{T_0}{\log (1+t)}$。
    • $T_n=\frac{T_0}{1+t}$。

• 终止温度。当 $T_0$ 迭代到终止温度时就会结束退火。一般设为 eps=1e-k（$k\in {\mathbb{Z}}^{+}$）。

一般针对数据进行『温度参数』$T$，『降温参数』$\Delta$ 的调参，在本地手造大数据跑，自己抉择。

对时间和正确性的平衡选取。

有的时候可以用 #include <ctime> 库里面自带的 clock() 函数计时，也可以自己定一个跑的次数。

( clock() / (1.0 * CLOCKS_PER_SEC) ) <= TIME
//返回的是多少秒 所以TIME是个 <1 的浮点数

需要注意是：

• 初始温度 $T_0$ 的选取对算法结果有一定的影响，最好是多次运行对结果进行综合判断。
• 在算法运行初期，温度下降快，避免接受过多的差结果。当运行时间增加，温度下降减缓，以便于更快稳定结果。
• 当迭代次数增加到一定次数时，结果可能已经达到稳定，但是距离算法结束还有一段时间。在设计程序时应该加入适当的输出条件，满足输出条件即可结束程序。

最后给出流程图总结：又淘了一张好图

显然，模拟退火也不一定是对的，这个概率接受就很概率。但对比爬山得到最优解的概率肯定是大大增加的。

例题

Strange function

hdu2899

$T$ 次询问，每次给定 $y$。

求 $f(x)=6x^7+8x^6+7x^3+5x^2-yx(0\le x\le 100)$ 的最小值。

#include <bits/stdc++.h>
using namespace std;
double y;
const double eps = 1e-8; //终止温度
const double delta = 0.997; //温度变化率
mt19937 wwl(time(0));
uniform_real_distribution < double > range( 0, 100 );double f( double x ) {return 6 * pow(x, 7) + 8 * pow(x, 6) + 7 * pow(x, 3) + 5 * pow(x, 2) - y * x;
}double solve() {double T = 100, x = range( wwl ); //初始温度 以及初始随机解double now = f(x), ans = now;int Time = 8e5; //防止超时的卡点次数while( T > eps and Time -- ) { //要么降温完成 要么被卡时double tx = x + (rand() * 2 - RAND_MAX) * T; //随机扰动产生新解if( 0 <= tx and tx <= 100 ) {double nxt = f(tx);ans = min( ans, nxt );if( nxt < now ) //新状态更小 直接接受x = tx, now = nxt;else if( rand() < exp( ( now - nxt ) / T ) * RAND_MAX ) //在一定概率内仍接受这个解x = tx, now = nxt;}T *= delta; //降温}return ans;
}int main() {int T;scanf( "%d", &T );while( T -- ) {scanf( "%lf", &y );printf( "%.4f\n", solve() );}return 0;
}

[JSOI2004]平衡点 / 吊打XXX

洛谷链接

#include <bits/stdc++.h>
using namespace std;
#define delta 0.996
#define maxn 1005
#define eps 1e-15
struct node { int x, y, w; }g[maxn];
int n;double energy( double x, double y ) {double ans = 0, dx, dy;for( int i = 1;i <= n;i ++ ) {dx = x - g[i].x, dy = y - g[i].y;ans += sqrt( dx * dx + dy * dy ) * g[i].w;}return ans;
}double ansx, ansy, ans, x, y, now;
void Simulate_Anneal() {double T = 5e4;while( T > eps ) {double tx = x + (rand() * 2 - RAND_MAX) * T;double ty = y + (rand() * 2 - RAND_MAX) * T;double tw = energy( tx, ty );if( tw < ans ) ans = tw, ansx = tx, ansy = ty;if( tw < now ) x = tx, y = ty, now = tw;else if( rand() < exp( ( now - tw ) / T ) * RAND_MAX )x = tx, y = ty;T *= delta;}
}signed main() {scanf( "%d", &n );for( int i = 1;i <= n;i ++ )scanf( "%d %d %d", &g[i].x, &g[i].y, &g[i].w );for( int i = 1;i <= n;i ++ ) x += g[i].x, y += g[i].y;x /= n, y /= n;ansx = x, ansy = y;now = ans = energy( x, y );Simulate_Anneal();Simulate_Anneal();Simulate_Anneal();Simulate_Anneal();printf( "%.3f %.3f\n", ansx, ansy );return 0;
}

Haywire

洛谷链接

#include <bits/stdc++.h>
using namespace std;
#define TIME 0.9
#define eps 1e-10
#define delta 0.998
#define maxn 15
int n;
int p[maxn];
int f[maxn][5];int energy() {int ans = 0;for( int i = 1;i <= n;i ++ )for( int j = 1;j <= 3;j ++ )ans += fabs( p[i] - p[f[i][j]] );return ans;
}int main() {mt19937 wwl(time(NULL));scanf( "%d", &n );uniform_int_distribution < int > id( 1, n );for( int i = 1;i <= n;i ++ )for( int j = 1;j <= 3;j ++ )scanf( "%d", &f[i][j] );iota( p + 1, p + n + 1, 1 );int ans = energy();while( ( clock() / (1.0 * CLOCKS_PER_SEC) ) <= TIME ) {for( int i = 1;i <= n;i ++ ) p[i] = i;double T = 1e5; int x, y;while( T > eps ) {do { x = id( wwl ), y = id( wwl ); }while( x == y );swap( p[x], p[y] );int now = energy();if( now < ans ) ans = now;else if( rand() > exp( ( now - ans ) / T ) * RAND_MAX )swap( p[x], p[y] );T *= delta;}}printf( "%d\n", ans / 2 );return 0;
}

学习参考博客：

https://www.cnblogs.com/flashhu/p/8884132.html

https://blog.csdn.net/weixin_42398658/article/details/84031235

https://zhuanlan.zhihu.com/p/266874840?utm_source=qq