算法2.1: 最快上升爬山法
x0 <- 随机生成的个体
while not ( 终止准则)计算x0的适应度f(x0)For 每一个解的特征 q=1,2,,...nxq <- x0 用一个随机变异替换xq的第q个特征计算xq的适应度f(xq)获取下一个更优的解:寻找使f(xq)最大的xq, 令其等于x', x' <- argmax(f(xq)): q 属于[0,n]if x0 != x' thenx0 <- x'else:x0 保持不变算法理解:该算法比较保守,每次只变化解的一个特征,并用某一个最好的特征变化来代替当前的解
终止准则:1. 迭代次数 2. 迭代解之间的差距和迭代次数,如迭代多少次之后,并且每次迭代解之间差距很小的时候就可以终止
代码实现及仿真:
def objective_function(x, y):c = 2 * math.pisum1 = 0sum2 = 0term1 = -0.2 * math.sqrt((x ** 2 + y ** 2) / 2)term2 = math.exp((math.cos(c * x) + math.cos(c * y)) / 2)y = math.exp(1) - 20 * math.exp(term1) - term2return ydef fastest_climb_mountains(func, times=1000):""" fastest climb mountains algorithm """x = [-5, 5]x0 = [rd.uniform(-5, 5), rd.uniform(-5, 5)]i = 1res = []while i <= times:f_x0 = func(x0[0], x0[1])f_xq = [0, 0]xq_1 = copy.deepcopy(x0)xq_2 = copy.deepcopy(x0)xq = [xq_1, xq_2]for j in range(2):xq[j][j] = rd.uniform(-5, 5)f_xq[j] = func(xq[j][0], xq[j][1])xq.append(x0)f_xq.append(f_x0)min_index = np.nanargmin(f_xq)new_f_x0 = f_xq[min_index]new_x0 = xq[min_index]if new_f_x0 != f_x0:x0 = copy.deepcopy(new_x0)res.append(func(x0[0], x0[1]))i += 1x_i = np.linspace(0, times, times)plt.title("Ackley function")plt.xlabel("x axis number of iterations")plt.ylabel("y axis objective value")plt.plot(x_i, res)plt.show()if __name__ == '__main__':fastest_climb_mountains(objective_function)仿真结果:

算法2.2: 依次上升爬山法
x0 <- 随机生成的个体
while not ( 终止准则)计算x0的适应度f(x0)replaceFlag = falseFor 每一个解的特征 q=1,2,,...nxq <- x0 用一个随机变异替换xq的第q个特征计算xq的适应度f(xq)if f(xq) > f(x0):x0 <- xqreplaceFlag = trueendif获取下一个更优的解:寻找使f(xq)最大的xq, 令其等于x', x' <- argmax(f(xq)): q 属于[0,n]if not replaceFlag thenx0 保持不变endif 算法理解:该算法比较贪婪,每次只变化解的一个特征,只要变化的某一个特征比当前解好,那么就会替换当前的解
def ascending_climb_mountains(func, times=1000):x = [-5, 5]x0 = [rd.uniform(-5, 5), rd.uniform(-5, 5)]i = 1res = []while i <= times:f_x0 = func(x0[0], x0[1])minf = f_x0for j in range(2):xq = copy.deepcopy(x0)xq[j] = rd.uniform(-5, 5)f_xq = func(xq[0], xq[1])if f_xq < f_x0:x0 = copy.deepcopy(xq)f_x0 = func(x0[0], x0[1])replace = Trueres.append(f_x0)i += 1x_i = np.linspace(0, times, times)plt.title("Ackley function")plt.xlabel("x axis number of iterations")plt.ylabel("y axis objective value")plt.plot(x_i, res)plt.show()相同的例子,算法2.2的仿真结果如下:

算法2.3: 随机变异爬山法
x0 <- 随机生成的个体
while not ( 终止准则)计算x0的适应度f(x0)q <- 从[1,n] 中随机选择解的特征x1 <- x0用一个随机变异的值替换x1的第q个特征计算x1的适应度f(x1)if f(x1) > f(x0):x0 <- x1endif算法实现:
def random_mutation_climb_mountains(func, times=1000):x = [-5, 5]x0 = [rd.uniform(-5, 5), rd.uniform(-5, 5)]i = 1res = []while i <= times:f_x0 = func(x0[0], x0[1])q = rd.randint(0, 1)x1 = copy.deepcopy(x0)x1[q] = rd.uniform(-5, 5)f_x1 = func(x1[0], x1[1])if f_x1 < f_x0:x0 = copy.deepcopy(x1)f_x0 = func(x0[0], x0[1])res.append(f_x0)i += 1x_i = np.linspace(0, times, times)plt.title("Ackley function")plt.xlabel("x axis number of iterations")plt.ylabel("y axis objective value")plt.plot(x_i, res)plt.show()算法理解:随机变异每次随机的选取变异的特征,每次迭代只需要计算一次适应度的值。

算法2.4: 自适应爬山法
初始化 pm 属于 [0,1] 作为变异概率
x0 <- 随机生成的个体
while not ( 终止准则)计算x0的适应度f(x0)x1 <- x0For 每一个解的特征 q = 1,2,3...,n生成一个均匀分布的随机数r 属于[0, 1]if r < pm then用一个随机变异替换x1的第q个特征endif计算x1的适应度f(x1)if f(x1) > f(x0):x0 <- x1endif算法实现:
def adaptive_climb_mountains(func, times=1000, pm=0.3):x = [-5, 5]x0 = [rd.uniform(-5, 5), rd.uniform(-5, 5)]i = 1res = []f_x0 = func(x0[0], x0[1])while i <= times:x1 = copy.deepcopy(x0)for j in range(2):r = rd.uniform(0, 1)if r < pm:x1[j] = rd.uniform(-5, 5)f_x1 = func(x1[0], x1[1])if f_x1 < f_x0:x0 = copy.deepcopy(x1)f_x0 = func(x0[0], x0[1])res.append(f_x0)i += 1x_i = np.linspace(0, times, times)plt.title(f"Ackley function, pm={pm}")plt.xlabel("x axis number of iterations")plt.ylabel("y axis objective value")plt.plot(x_i, res)plt.show()试验结果:

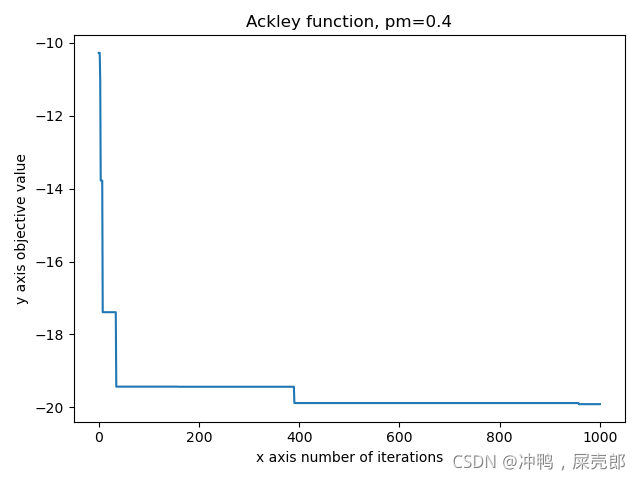
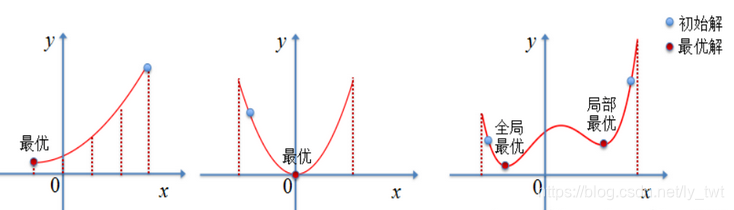
总结:爬山法可以用来求解确定性方法无法求解的优化问题,也跟更容易得到全局解,只要迭代次数足够多,但是每次的收敛速度可能是不一样的(将相同的代码运行多次,收敛速度不同,但是最后都收敛到了最优解)