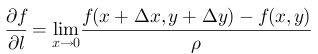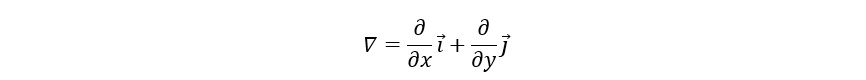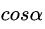梯度与导数的关系

梯度方向指向数值增长最快的方向，大小为变化率。通过这个性质也说明梯度是有方向和大小的矢量。通过梯度的定义我们发现，梯度的求解其实就是求函数偏导的问题，而我们高中所学的导数在非严格意义上来说也就是一元的“偏导”。通过这一点我们自然而然地想到梯度应该是导数向更高维数的推广。换句话说，梯度是矢量,而某点的导数是个常量。

梯度下降算法

如果函数 $f(\theta )$是凸函数，那么就可以使用梯度下降算法进行优化。梯度下降算法的公式：
$$\theta ={\theta }_0-\eta \cdot ▽f(\theta )$$
${\theta }_0$是更新前的$\theta$；$\eta$是学习因子，即步进长度；$▽f(\theta )$是方向。

梯度方向是上升方向

这个示例函数是$f(x)=(x-2{)}^2+2$
在（1，3）位置的梯度为-2<0，梯度方向为x轴的负方向，上升
在（3，3）位置的梯度为2>0,梯度方向为x轴正方向，上升
定义解释：
设f(x)有一阶导:$\frac{f(x+\Delta x)-f(x)}{\Delta x}\approx f^{\prime }(x)$。
如果f′(x)>0，在Δx邻域半径内单调上升，梯度方向取x的正方向，函数梯度上升。
如果f′(x)<0，在Δx邻域半径内单调下降，梯度方向取x的负方向，函数梯度上升。
梯度方向是上升方向，目标函数大多是loss函数，基本都是求最小值，那么就是就1取梯度的负方向。

一阶泰勒展开式与负梯度

梯度下降算法的推导如下：

其中， $\theta -{\theta }_0$是微小矢量，它的大小就是我们之前讲的步进长度$\eta$，$\eta$为标量，而$\theta -{\theta }_0$的单位向量用v表示。则$\theta -{\theta }_0$可表示为：$\theta -{\theta }_0=\eta v$。
特别需要注意的是， $\theta -{\theta }_0$不能太大，因为太大的话，线性近似就不够准确，一阶泰勒近似也不成立了。替换之后， $f(\theta )$的表达式为：
$$f(\theta )\approx f({\theta }_0)+\eta v\cdot ▽f(\theta )$$
局部下降的目的是希望每次$\theta$更新，都能让函数值 $f(\theta )$变小。也就是说，上式中，我们希望$f(\theta )<f({\theta }_0)$。则有：
$$f(\theta )-f({\theta }_0)\approx \eta v\cdot ▽f(\theta )<0$$
因为$\eta$为标量，且一般设定为正值，所以可以忽略，不等式变成了：$\eta v\cdot ▽f(\theta )<0$
$v$和$▽f(\theta )$都是向量，$▽f(\theta )$是当前位置的梯度方向，$v$表示下一步前进的单位向量。
假设AB均为向量， $\alpha$为两个向量之间的夹角。A和B的乘积为：
$$A\cdot B=\Vert A\Vert \cdot \Vert B\Vert \cdot cos(\alpha )$$
$\Vert A\Vert$和$\Vert B\Vert$ 均为标量，在$\Vert A\Vert$和$\Vert B\Vert$确定的情况下，只要$cos(\alpha )=-1$，即A和B完全反向，就能让A和B的向量乘积最小（负最大值）。即，当$v$与$▽f(\theta )$互为反向，即$v$为当前梯度方向的负方向的时候，能让$v\cdot ▽f(\theta )$最大程度地小，也就保证了$v$的方向是局部下降最快的方向。