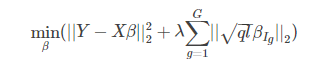python-sklearn岭回归与lasso回归模型代码实操

前言
一、岭回归
- 1.岭回归介绍
- 2.代码实现
- 3.岭回归参数调整
- 4.岭迹分析，可视化分析
二、LASSO回归
- 1.LASSO回归介绍
- 2.代码实现
- ps. Lasso回归的特征选择
- 3.岭回归参数调整
- 4.模型系数的数据可视化比较

前言

hello大家好这里是小L😊在这里想和大家一起学习一起进步。💪
这次笔记内容：学习岭回归与LASSO回归模型的sklearn实现。岭回归：平方和（L2正则化）；LASSO回归：绝对值（L1正则化）。
为了防止线性回归的过拟合，加了正则化系数，系数可能有正有负，因此将他的绝对值或者平方和加起来，使得误差平方和最小。

一、岭回归

1.岭回归介绍

L2正则化
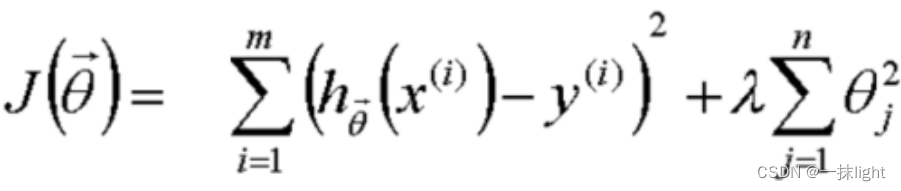
在这里插入图片描述

sklearn.linear_model.Ridge(

alpha=1：正则化因子（系数theta），入越大，越限制theta(即斜率k)越平缓，系数越小。系数越小误差越小。入越大，绝对值越接近于0。（限制x的发展，如果取0，x放飞)
fit_ intercept=True：截距，是否计算该模型截距。（除非数据标准化之后可false. ）
normalize=False：标准化false，标准化一般在建模之前做(sklearn.preprocessing.StandardScale)。
copy_X=True：原始的x还在，中间的用另一个存在。如false不要原来的x,新数据覆盖旧数据。
max_iter=None：最大迭代次数
tol =0.001:忍耐力，每努力一次提升的效果不大，提升没有超过0.001就停止
solver =‘auto’：提供很多方法

random_state：随机种子
）

属性

intercept_ ：截距
coef_ ：系数theta1到thetan,第几个自变量前面的系数，没有截距，只限制theta1–thetan来防止过拟合(决定斜率k),theta0(截距)没有关系
n_iter_:迭代多少次

方法

fit 训练
predict预测
score模型评估，不大于1，越大越好
get_params返回超参数的值
set_params修改超参数的值重新训练

2.代码实现

from sklearn.datasets import load_diabetes
diabetes=load_diabetes()#以糖尿病模型为例
X=diabetes.data#自变量
y=diabetes.target#因变量
from sklearn.model_selection import train_test_split#数据划分
X_train,X_test,y_train,y_test=train_test_split(X,y,random=8)

from sklearn.linear_model import Ridge#导入岭回归模型
ridge=Ridge()#模型实例化
ridge.fit(X_train,y_train)#模型训练
print("训练集的得分为：{:,2f}".format(ridge.score(X_train,y_train)))
print("测试集的得分为：{:,2f}".format(ridge.score(X_test,y_test)))

运行结果如下：

训练数据集得分:0.43
测试数据集得分:0.43

可以看出效果并不是很好，但是也不能因为一次结果否定这个模型，可以通过调参的方法，重新进行模型训练。

3.岭回归参数调整

#岭回归调参
#正则化系数alpha=10
ridge10=Ridge(alpha=10).fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(ridge10.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(ridge10.score(X_test,y_test)))

运行结果如下：

训练数据集得分:0.15
测试数据集得分:0.16

可以看出结果更加糟糕

#正则化系数alpha=0.1
ridge01=Ridge(alpha=0.1).fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(ridge01.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(ridge01.score(X_test,y_test)))

运行结果如下：

训练数据集得分:0.52
测试数据集得分:0.47

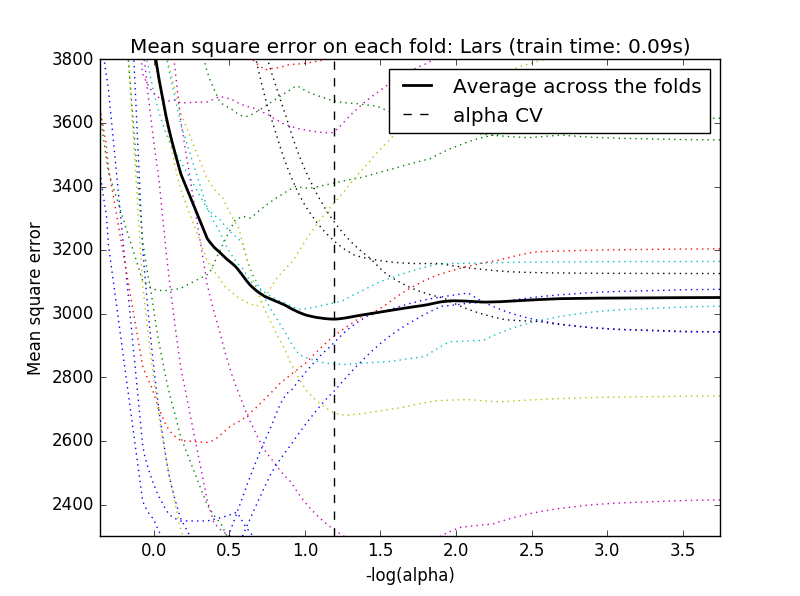
4.岭迹分析，可视化分析

#岭迹分析
#10个特征0-9，在4种回归的系数画出来
#模型系数的可视化比较
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(ridge.coef_,'s',label='Ridge alpha=1')
plt.plot(ridge10.coef_,'^',label='Ridge alpha=10')
plt.plot(ridge01.coef_,'v',label='Ridge alpha=0.1')
plt.plot(lr.coef_,'o',label='linear regression')
plt.xlabel("系数序号")
plt.ylabel("系数量级")
plt.hlines(0,0,len(lr.coef_))#hlines水平线从0到10（查）
plt.legend(loc='best')
plt.grid(linestyle=':')

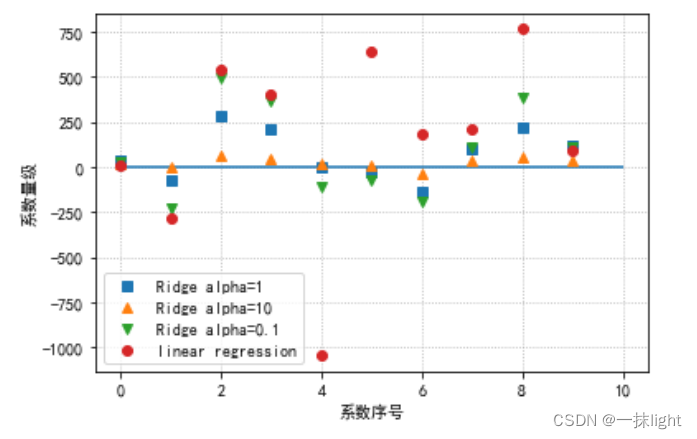
在这里插入图片描述

alpha越大，绝对值越接近于0。（限制x的发展，如果取0，x放飞)

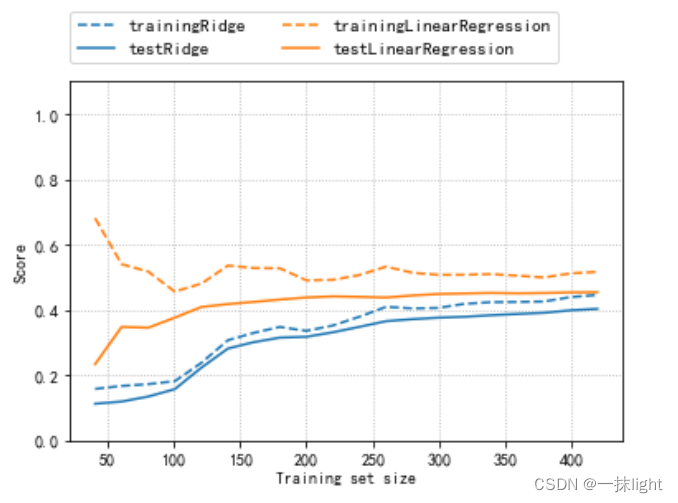
#绘制学习曲线：取固定alpha的值，改变训练集的数量
import numpy as np
from sklearn.model_selection import learning_curve,KFold
def plot_learning_curve(est,X,y):training_set_size,train_scores,test_scores=learning_curve(est,X,y,train_sizes=np.linspace(.1,1,20),cv=KFold(20,shuffle=True,random_state=1))estimator_name=est.__class__.__name__line=plt.plot(training_set_size,train_scores.mean(axis=1),'--',label='training'+estimator_name)plt.plot(training_set_size,test_scores.mean(axis=1),'-',label='test'+estimator_name,c=line[0].get_color())plt.xlabel('Training set size')plt.ylabel('Score')plt.ylim(0,1.1)
plot_learning_curve(Ridge(alpha=1),X,y)
plot_learning_curve(LinearRegression(),X,y)
plt.legend(loc=(0,1.05),ncol=2,fontsize=11)
plt.grid(linestyle=':')

在这里插入图片描述

二、LASSO回归

1.LASSO回归介绍

L1正则化
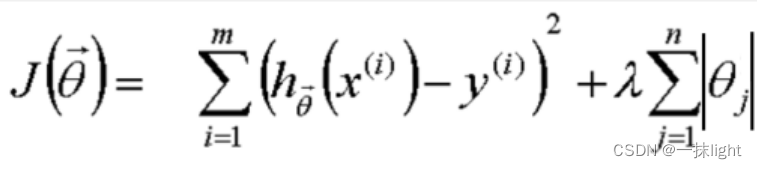
在这里插入图片描述

sklearn.linear_model.Lasso(

alpha=1：正则化因子（系数theta），入越大，越限制theta(即斜率k)越平缓，系数越小。系数越小误差越小。入越大，绝对值越接近于0。（限制x的发展，如果取0，x放飞)
fit_ intercept=True：截距，是否计算该模型截距。（除非数据标准化之后可false. ）
normalize=False：标准化false，标准化一般在建模之前做(sklearn.preprocessing.StandardScale)。
precompute=False
**copy_X=**True：原始的x还在，中间的用另一个存在。如false不要原来的x,新数据覆盖旧数据。
max_iter=1000：最大迭代次数
tol =0.0001:忍耐力，每努力一次提升的效果不大，提升没有超过0.001就停止
warm_start =True:下一次运行会从当前的点继续往下走，若False每次都重新运行一次[重新开始]（深度学习中经常有这个参数）
positive=False
random_state=None：随机种子
selection=‘cyclic’
）

2.代码实现

from sklearn.datasets import load_diabetes
diabetes=load_diabetes()#以糖尿病模型为例
X=diabetes.data#自变量
y=diabetes.target#因变量
from sklearn.model_selection import train_test_split#数据划分
X_train,X_test,y_train,y_test=train_test_split(X,y,random=8)

from sklearn.linear_model import Lasso#导入Lasso回归模块
lasso=Lasso()#模型实例化
lasso.fit(X_train,y_train)#模型训练
print("套索回归在训练集的得分为：{:,2f}".format(lasso.score(X_train,y_train)))
print("套索回归在测试集的得分为：{:,2f}".format(lasso.score(X_test,y_test)))

运行结果如下：

训练数据集得分:0.36
测试数据集得分:0.37

可以看出效果并不是很好，但是也不能因为一次结果否定这个模型，可以通过调参的方法，重新进行模型训练。

ps. Lasso回归的特征选择

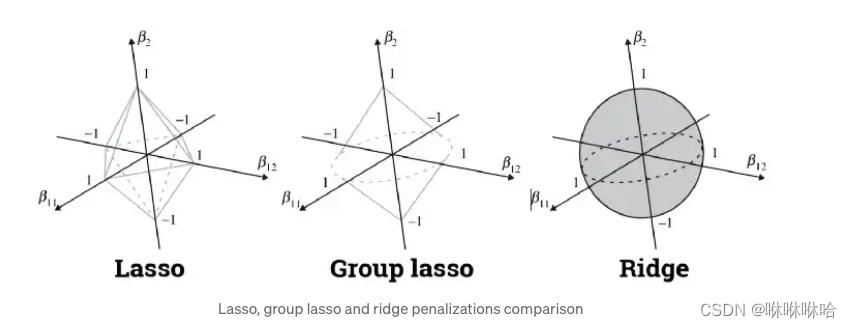
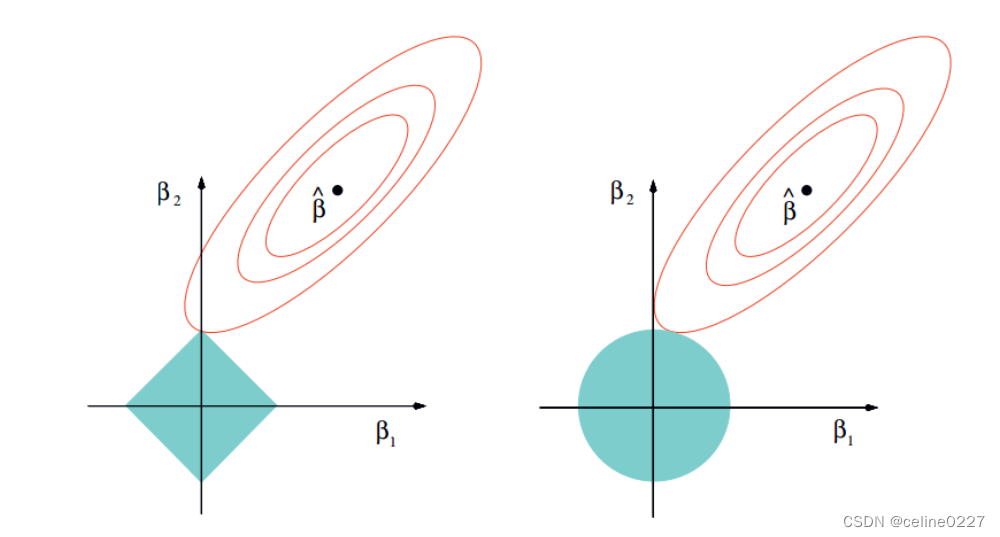
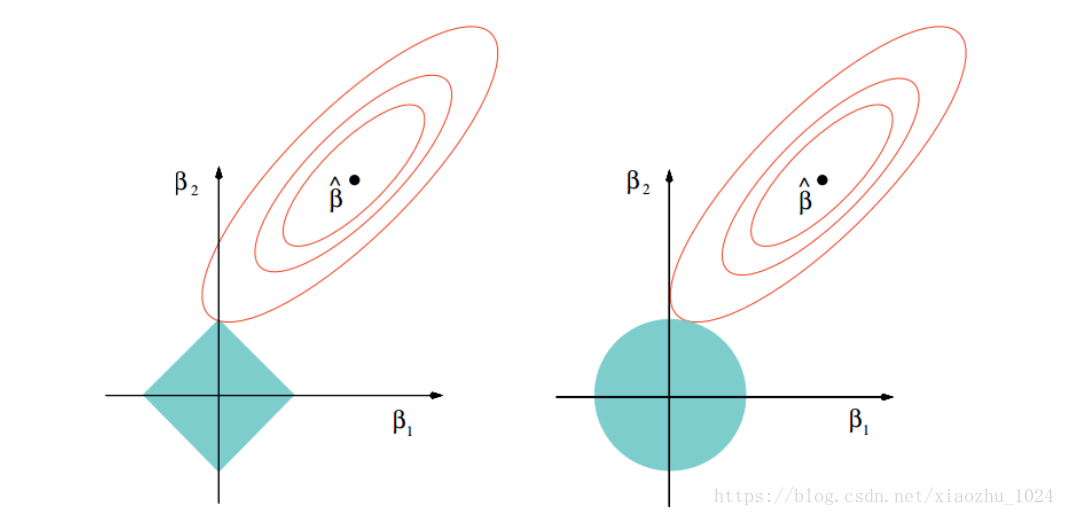
#岭回归圈圈（L2范数，里面可以有多个0,削尖，把很多特征都削成0），Lasso回归四条直线（L1范数方形）
lasso和岭回归，根据最小二乘法，最后需要使误差最小。
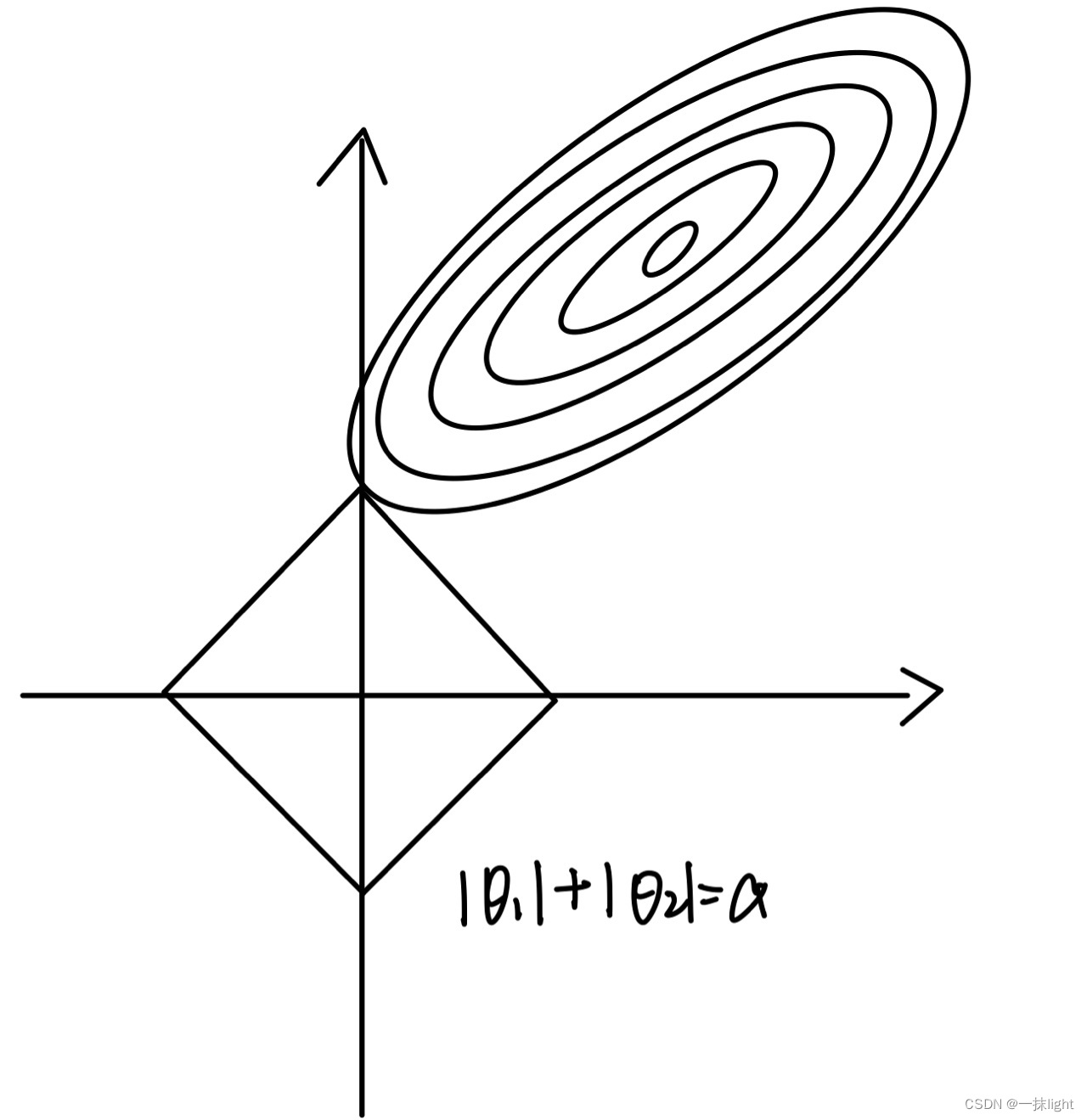
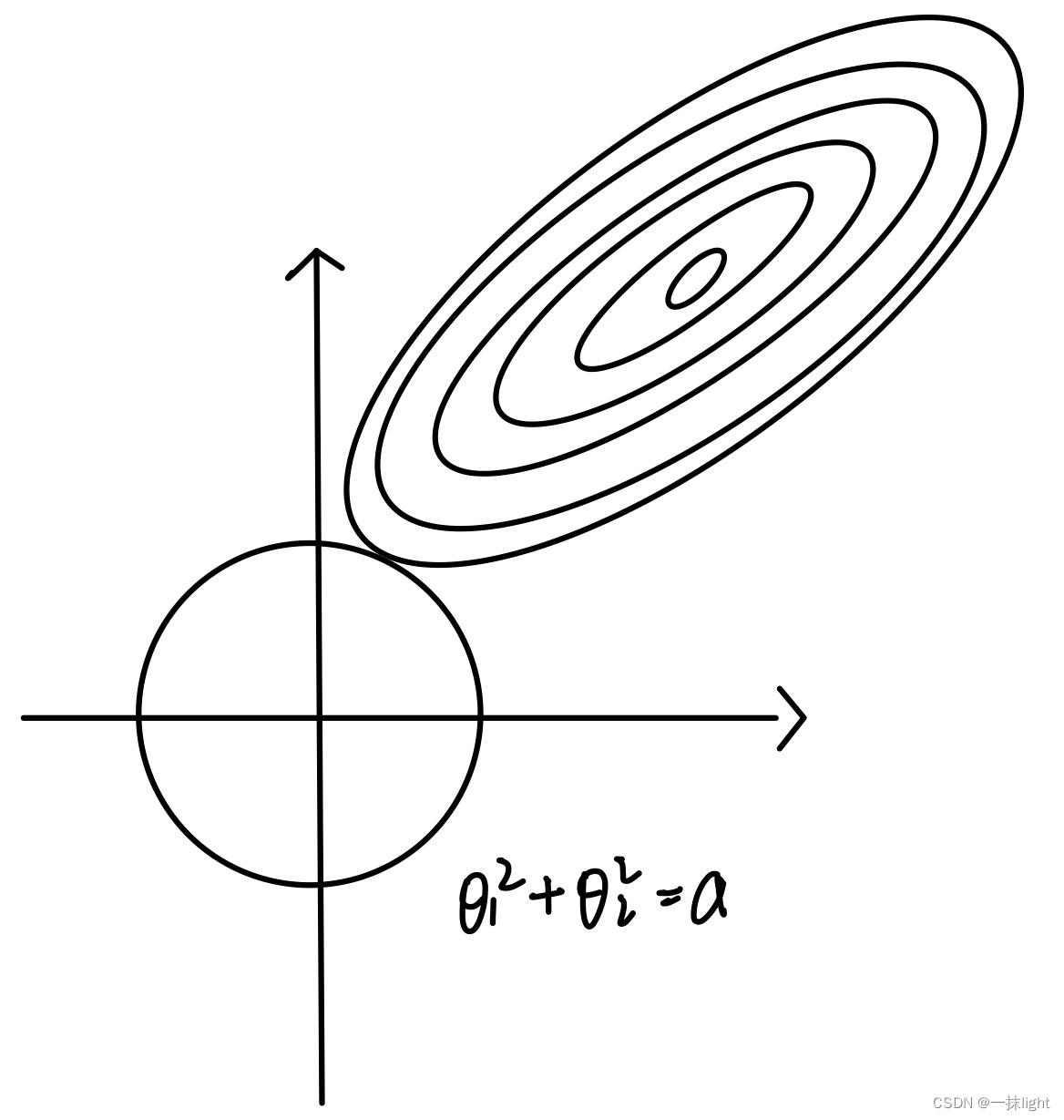
在这里插入图片描述

由于岭回归对w的限制空间是圆形的，lasso对w的限制空间是由棱角的。椭圆更容易切在w为某一维的图形为有棱角的图形，即Lasso回归模型。（圆形有凸起会阻挡切在0的位置）

LASSO回归相对于岭回归，更适合做特征选择。（面试问题）
怎样调节优化多个特征，选出更重要的特征，使得我们的精度更高

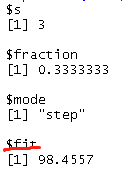
print("套索回归使用的特征数：{}".format(np.sum(lasso.coef_!=0)))

运行结果如下：

套索回归使用的特征数：3

比较一下岭回归和Lasso回归中能使用的特征数
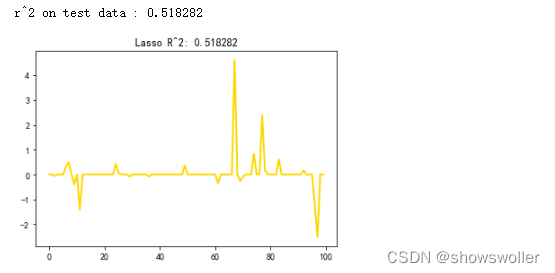
Lasso回归

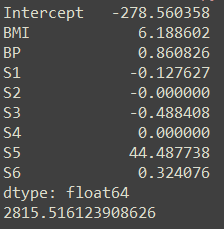
lasso.coef_

运行结果如下：

array([  0.        ,  -0.        , 384.73421807,  72.69325545,0.        ,   0.        ,  -0.        ,   0.        ,247.88881314,   0.        ])

岭回归

ridge.coef_

运行结果如下：

array([  36.8262072 ,  -75.80823733,  282.42652716,  207.39314972,-1.46580263,  -27.81750835, -134.3740951 ,   98.97724793,222.67543268,  117.97255343])

3.岭回归参数调整

#增大最大迭代次数的默认设置，（默认max_iter=1000）
lasso=Lasso(max_iter=100000)
lasso.fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(lasso.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(lasso.score(X_test,y_test)))
print("套索回归中使用的特征数:{}".format(lasso.score(X_test,y_test)))

运行结果如下：

训练数据集得分:0.36
测试数据集得分:0.37
套索回归中使用的特征数:0.36561858962128

可以看出结果并没有什么变化，所以换一个参数继续调参

#增加最大迭代次数的默认值设置，（默认max_iter=1000）
#同时调整alpha的值
lasso01=Lasso(alpha=0.1,max_iter=100000)
lasso01.fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(lasso01.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(lasso01.score(X_test,y_test)))
print("套索回归中使用的特征数:{}".format(lasso01.score(X_test,y_test)))

运行结果如下：

训练数据集得分:0.52
测试数据集得分:0.48
套索回归中使用的特征数:0.47994757514558173

继续尝试探索规律

#增加最大迭代次数的默认值设置，（默认max_iter=1000）
#同时调整alpha的值
lasso00001=Lasso(alpha=0.0001,max_iter=100000)
lasso00001.fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(lasso00001.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(lasso00001.score(X_test,y_test)))
print("套索回归中使用的特征数:{}".format(lasso00001.score(X_test,y_test)))

结果如下：

训练数据集得分:0.53
测试数据集得分:0.46
套索回归中使用的特征数:0.4594509683706015

alpha越大，选的特征越少。alpha=0时，普通的线性回归（限制x的发展，如果取0，x放飞)

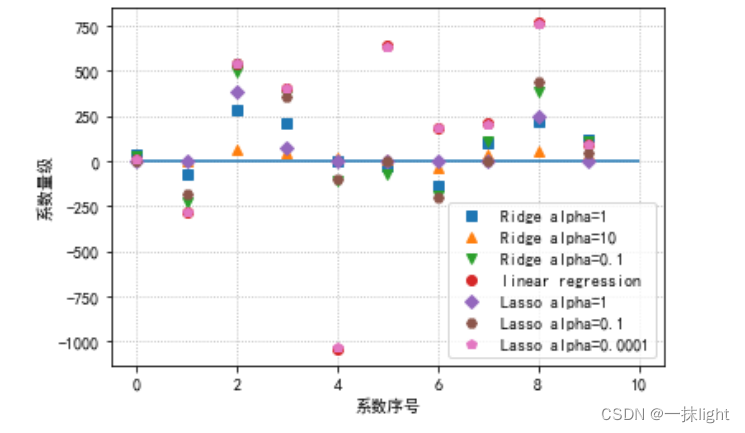
4.模型系数的数据可视化比较

plt.plot(ridge.coef_,'s',label='Ridge alpha=1')
plt.plot(ridge10.coef_,'^',label='Ridge alpha=10')
plt.plot(ridge01.coef_,'v',label='Ridge alpha=0.1')
plt.plot(lr.coef_,'o',label='linear regression')plt.plot(lasso.coef_,'D',label='Lasso alpha=1')
plt.plot(lasso01.coef_,'H',label='Lasso alpha=0.1')
plt.plot(lasso00001.coef_,'p',label='Lasso alpha=0.0001')plt.xlabel("系数序号")
plt.ylabel("系数量级")
plt.hlines(0,0,len(lr.coef_))#hlines水平线从0到10（查）
plt.legend(loc='best')
plt.grid(linestyle=':')