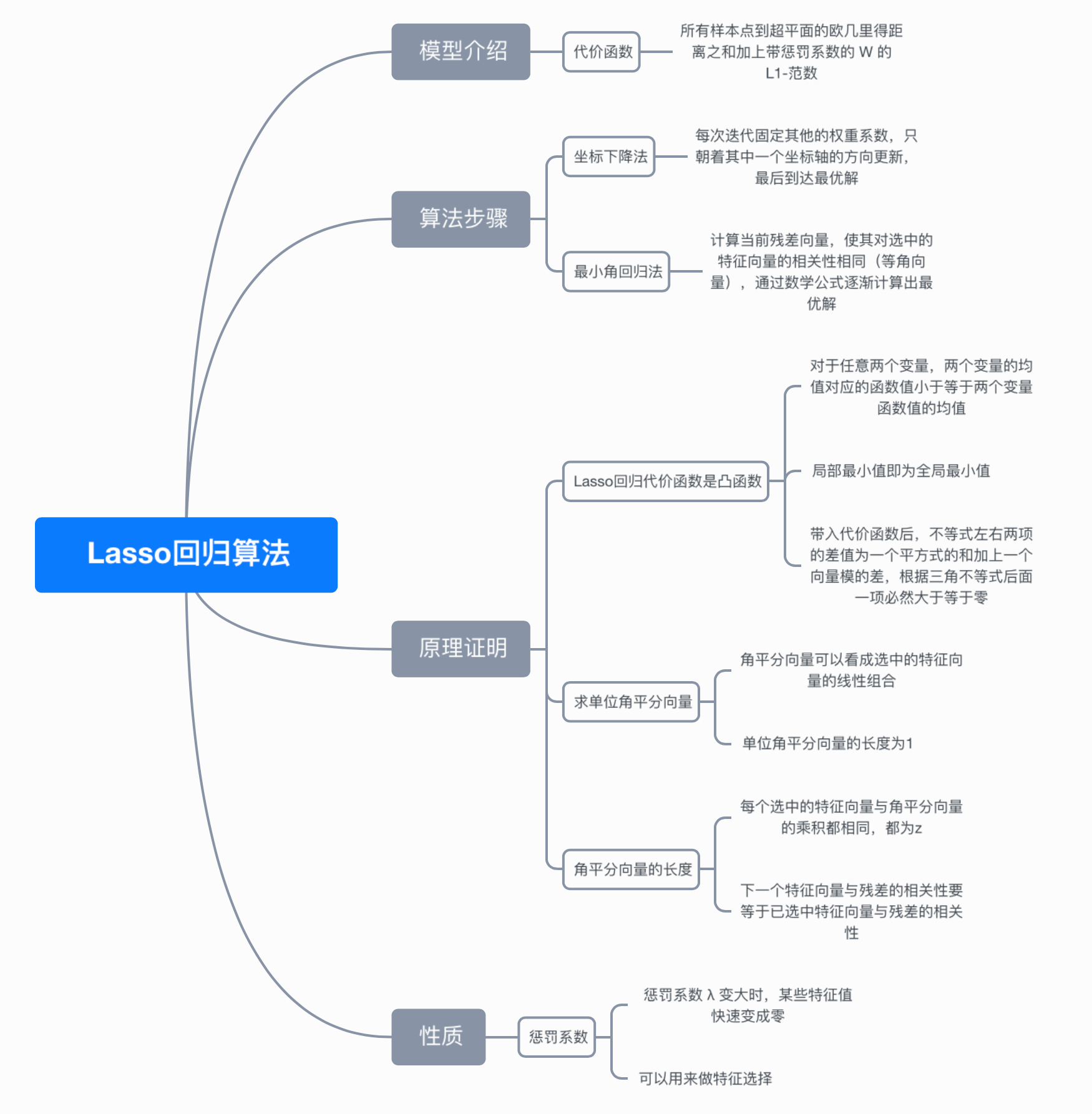
1. 概念

一直看一遍忘一遍，实在懒得再查了，理解后再次整理，希望能加深理解。

先总结几个概念：

回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。

为什么要回归分析？

1. 它表明自变量和因变量之间的显著关系；
2. 它表明多个自变量对一个因变量的影响强度。
   回归分析允许我们去比较那些衡量不同尺度的变量之间的相互影响，如价格变动与促销活动数量之间联系。这些有利于数据分析人员以及数据科学家排除并估计出一组最佳的变量，用来构建预测模型。
   常见的回归模型很多，在此我对自己常用的进行整理。

2. logistic回归

引用一篇整理不错的博客，传送门，核心看点是：

1. logit变换
2. logistic模型和二项逻辑回归模型
3. 损失函数
4. logistic回归模型的评价

3. 多重共线性问题

在介绍Lasso回归和ridge回归之前，我们先解释一个名词，那就是多重共线性，在进行线性回归分析时，容易出现自变量（解释变量）之间彼此相关的现象，我们称这种现象为多重共线性。适度的多重共线性不成问题，但当出现严重共线性问题时，会导致分析结果不稳定，出现回归系数的符号与实际情况完全相反的情况。本应该显著的自变量不显著，本不显著的自变量却呈现出显著性，这种情况下就需要消除多重共线性的影响。

出现的原因： 多重共线性问题就是指一个解释变量的变化引起另一个解释变量地变化。原本自变量应该是各自独立的，根据回归分析结果，能得知哪些因素对因变量Y有显著影响，哪些没有影响。如果各个自变量x之间有很强的线性关系，就无法固定其他变量，也就找不到x和y之间真实的关系了。

除此以外，多重共线性的原因还可能包括：

1. 数据不足。在某些情况下，收集更多数据可以解决共线性问题。
2. 错误地使用虚拟变量。（比如，同时将男、女两个虚拟变量都放入模型，此时必定出现共线性，称为完全共线性）

如何判断共线性程度？ 有多种方法可以检测多重共线性，较常使用的是回归分析中的VIF值，VIF值越大，多重共线性越严重。一般认为VIF大于10时（严格是5），代表模型存在严重的共线性问题。

多重共线性处理方法：

1. 手动移除出共线性的变量
2. 逐步回归法
3. 增加样本容量
4. 岭回归
   具体细节介绍请参考：传送门

4. ridge回归和Lasso回归

岭回归(ridge regression, Tikhonov regularization) 是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

Lasso回归的全称是Least Absolute Selection and Shrinkage Operator， 即最小绝对值选择与收缩算子。Lasso方法是以缩小变量集（降阶）为思想的压缩估计方法。它通过构造一个惩罚函数，可以将变量的系数进行压缩并使某些回归系数变为0，进而达到变量选择的目的。两种回归都可以用来解决标准线性回归的过拟合问题。

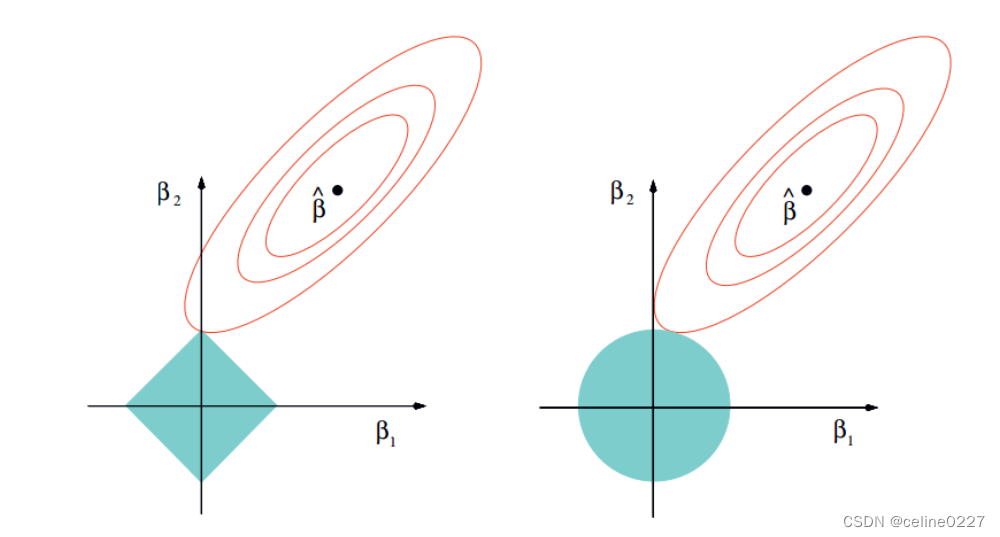
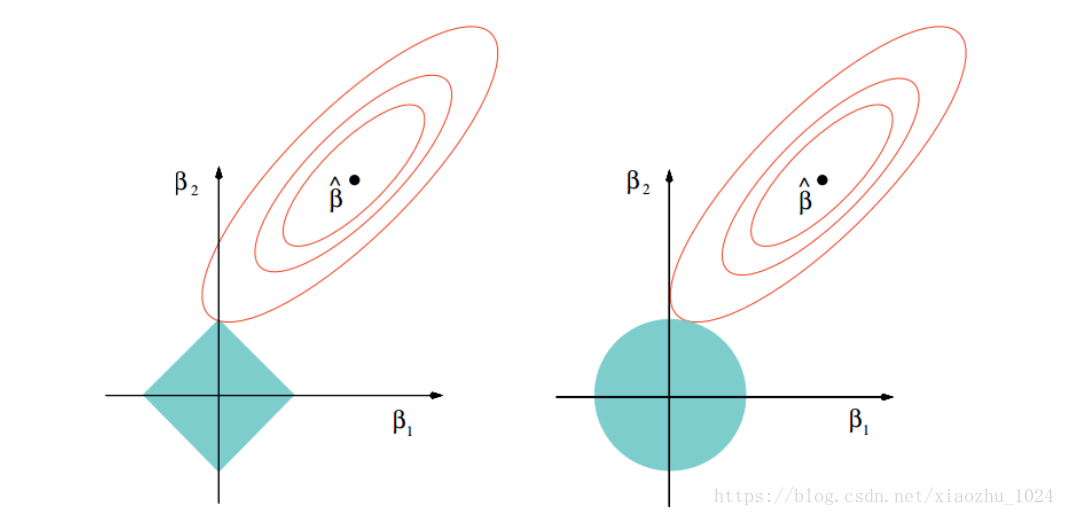
二者核心的差别就是，lasso回归使用了一范数，而岭回归使用了二范数，二者的核心差异。

二者具体的细节，参考这篇两篇内容，细节拉满，浅显易懂：
传送门1
传送门2

5. Elastic Net

为什么会出现Elastic Net？

岭回归与 Lasso 回归两种正则化的方法，当多个特征存在相关时，Lasso 回归可能只会随机选择其中一个，岭回归则会选择所有的特征。这时很容易的想到如果将这两种正则化的方法结合起来，就能够集合两种方法的优势，这种正则化后的算法就被称为弹性网络回归。

具体使用，参考这篇博客，讲解的比较细致，传送门

6. 总结

遇到一个问题，只能解决一个问题，当我把它串在了一起，就学习了好几个问题，借鉴居多，看完记得回来交流啊！

7. 再补充学习代码部分

此处参考博客：https://blog.csdn.net/Santorinisu/article/details/104449791

导包和数据读取划分阶段

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")plt.rcParams['figure.dpi']=200
plt.rcParams['savefig.dpi']=200
font = {'family': 'Times New Roman','weight': 'light'}
plt.rc("font", **font)#Section 1: Load data and split it into Train/Test dataset
price=datasets.load_boston()
X=price.data
y=price.targetX_train,X_test,y_train,y_test=train_test_split(X, y, test_size=0.3)

Ridge Regression（岭回归）

from sklearn.linear_model import Ridgeridge=Ridge(alpha=1.0)
ridge.fit(X_train,y_train)
y_train_pred=ridge.predict(X_train)
y_test_pred=ridge.predict(X_test)plt.scatter(y_train_pred,y_train_pred-y_train,c='blue',marker='o',edgecolor='white',label='Training Data')
plt.scatter(y_test_pred,y_test_pred-y_test,c='limegreen',marker='s',edgecolors='white',label='Test Data')
plt.xlabel("Predicted Values")
plt.ylabel("The Residuals")
plt.legend(loc='upper left')
plt.hlines(y=0,xmin=-10,xmax=50,color='black',lw=2)
plt.xlim([-10,50])
plt.title("Ridge Regression Model")
plt.savefig('./fig2.png')
plt.show()print("\nMSE Train in Ridge: %.3f, Test: %.3f" % \(mean_squared_error(y_train,y_train_pred),mean_squared_error(y_test,y_test_pred)))print("R^2 Train in Ridge: %.3f, Test: %.3f" % \(r2_score(y_train,y_train_pred),r2_score(y_test,y_test_pred)))

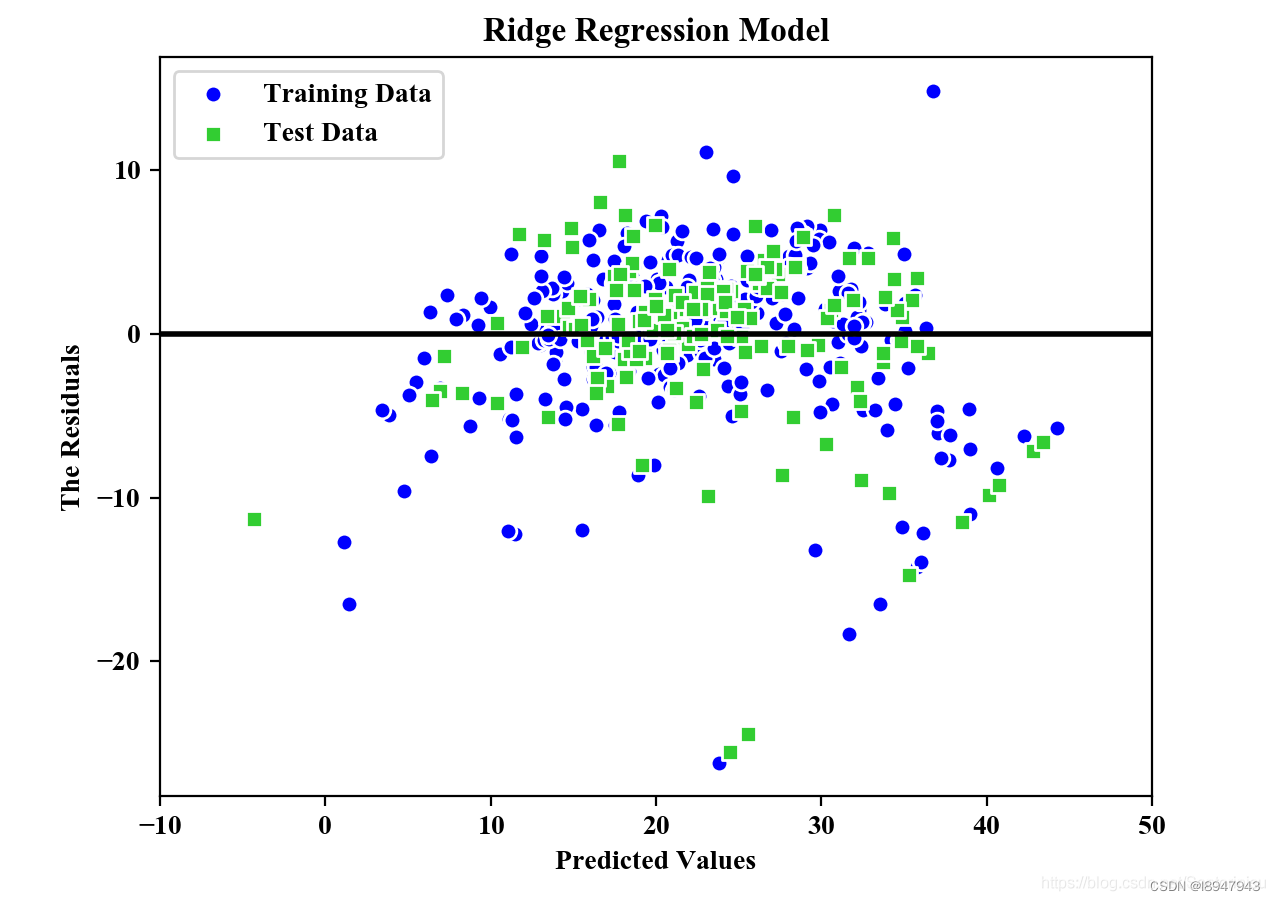
预测结果

MSE Train in Ridge: 20.889, Test: 25.470
R^2 Train in Ridge: 0.739, Test: 0.728

LASSO Regression（lasso回归）

#Section 2.2: LASSO Model
#The parameter alpha would be the regulation stength.
from sklearn.linear_model import Lassolasso=Lasso(alpha=1.0)
lasso.fit(X_train,y_train)
y_train_pred=lasso.predict(X_train)
y_test_pred=lasso.predict(X_test)plt.scatter(y_train_pred,y_train_pred-y_train,c='blue',marker='o',edgecolor='white',label='Training Data')
plt.scatter(y_test_pred,y_test_pred-y_test,c='limegreen',marker='s',edgecolors='white',label='Test Data')
plt.xlabel("Predicted Values")
plt.ylabel("The Residuals")
plt.legend(loc='upper left')
plt.hlines(y=0,xmin=-10,xmax=50,color='black',lw=2)
plt.xlim([-10,50])
plt.title("LASSO Regression Model")
plt.savefig('./fig3.png')
plt.show()print("\nMSE Train in LASSO: %.3f, Test: %.3f" % (mean_squared_error(y_train,y_train_pred), mean_squared_error(y_test,y_test_pred)))
print("R^2 Train in LASSO: %.3f, Test: %.3f" % (r2_score(y_train,y_train_pred), r2_score(y_test,y_test_pred)))

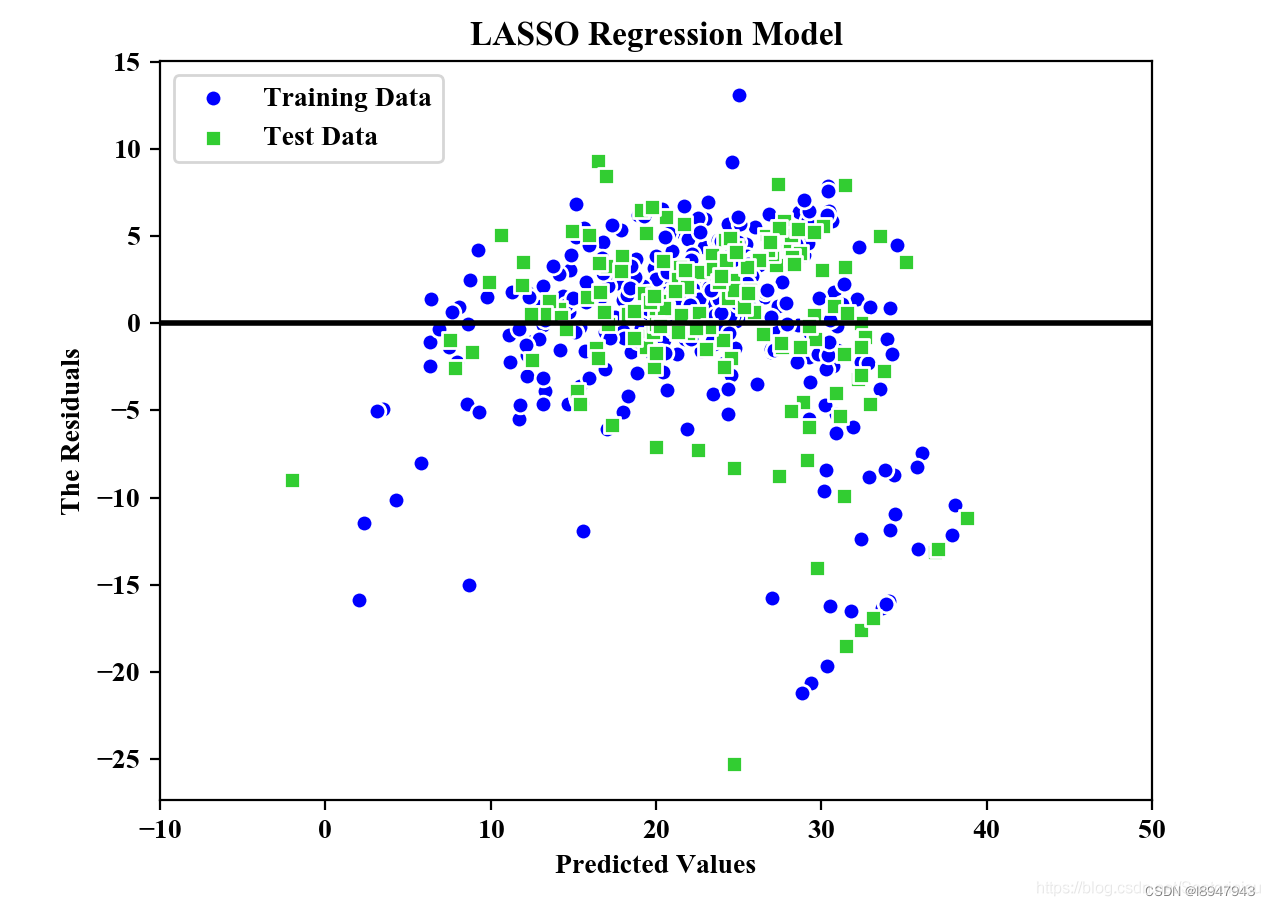
MSE Train in LASSO: 25.618, Test: 32.727
R^2 Train in LASSO: 0.680, Test: 0.650

ElasticNet Regression（弹性网络回归）

#Section 2.3: Elastic Net Model
#The parameter alpha would be the regulation stength.
from sklearn.linear_model import ElasticNetelastic_net=ElasticNet(alpha=1.0,l1_ratio=0.5)
elastic_net.fit(X_train,y_train)
y_train_pred=elastic_net.predict(X_train)
y_test_pred=elastic_net.predict(X_test)plt.scatter(y_train_pred,y_train_pred-y_train,c='blue',marker='o',edgecolor='white',label='Training Data')
plt.scatter(y_test_pred,y_test_pred-y_test,c='limegreen',marker='s',edgecolors='white',label='Test Data')
plt.xlabel("Predicted Values")
plt.ylabel("The Residuals")
plt.legend(loc='upper left')
plt.hlines(y=0,xmin=-10,xmax=50,color='black',lw=2)
plt.xlim([-10,50])
plt.title("ElasticNet Regression Model")
plt.savefig('./fig4.png')
plt.show()print("\nMSE Train in ElasticNet: %.3f, Test: %.3f" % (mean_squared_error(y_train,y_train_pred), mean_squared_error(y_test,y_test_pred)))
print("R^2 Train in ElasticNet: %.3f, Test: %.3f" % (r2_score(y_train,y_train_pred), r2_score(y_test,y_test_pred)))

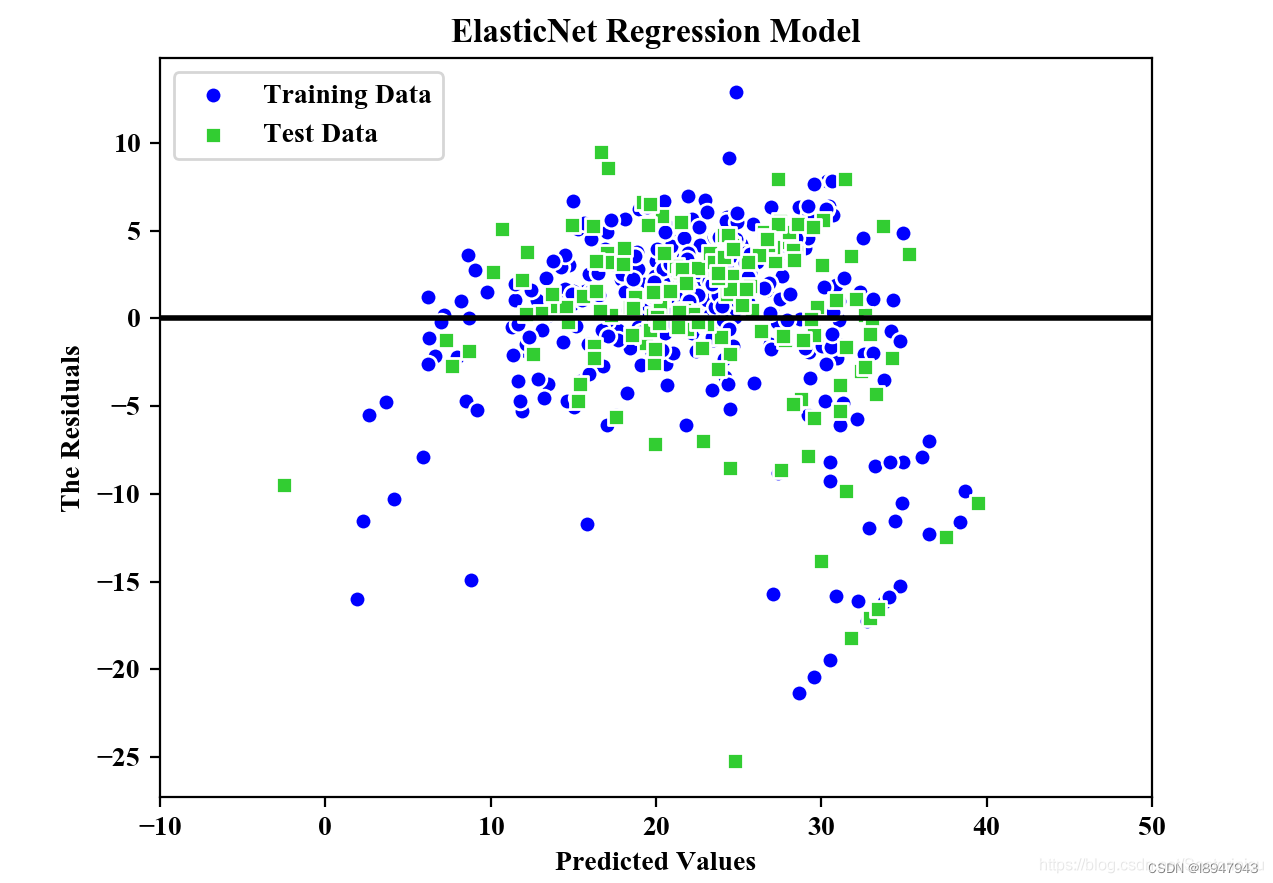
MSE Train in ElasticNet: 24.999, Test: 31.943
R^2 Train in ElasticNet: 0.688, Test: 0.659

参考博客：

1. https://blog.csdn.net/sai_simon/article/details/122376407
2. https://zhuanlan.zhihu.com/p/400443773
3. https://www.cnblogs.com/Belter/p/8536939.html
4. https://zhuanlan.zhihu.com/p/72722146
5. http://t.csdn.cn/bl4fw
6. https://blog.csdn.net/Santorinisu/article/details/104449791