1.1.3. Lasso

一、简介

在这里插入图片描述

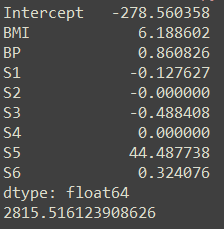
首先，Lasso同样是线性回归的一种变体。而文档中指出，它是一种能让参数 $\omega$ 稀疏的模型（作用）。它是压缩感知领域的基础（地位），在特定情况下，它可以“恢复一组非零权重的精确集”（这句话来自别人的翻译，我暂时还不明白）。

二、损失函数特性

在Ridge Regression中，我们介绍了正则项（惩罚项）。Lasso和Ridge模型上的差别也主要体现在损失函数中不同的正则项上。

首先，在Ridge中，为了约束参数 $\omega$ ，我们给损失函数添上了关于 $\omega$ 的 $l_2-norm$ （L2范数）。二范数，决定了他在限制参数 $\omega$ 的同时，也会尽可能保留每一个参数。这是它的优势，可以尽可能的保留信息，但是，在遇到特征数目很多时，他也会因为模型过于复杂而受限。

而在Lasso中，我们用 $\omega$ 的 $l_1-norm$ （L1范数）来有意的让特征稀疏化（这是L1范数的特性），从而简化模型的复杂度，或者在特征数（维数）远大于样本数时使用。

其次，我们注意到，Lasso的损失函数MSE部分乘上了系数 $1/2*n_{sample}$ 。这似乎有两个作用：

系数对MSE做了归一化，使得我们能够更好的比较不同模型之间的性能。（事实上，在求解单个模型的过程中，我们并不在意loss函数具体的值，我们只care变量在哪一点取最小值。）
对比MSE和正则项的比例，我们发现，当样本数目 $n_{sample}$ 越大时，正则项对损失函数的影响也就越大。（这也很好理解，因为样本数目越多时，我们越希望求得的参数稀疏，从而给模型带来更好的性能。）

三、求解Lasso模型

因为Lasso模型的损失函数中带有L1范数，所以它并不是处处可导的，我们也就不能采用常规的梯度下降法。

我所知的有三种求解Lasso模型的算法。

3.1坐标梯度下降

坐标梯度下降(coordinate descent)是sklearn求解Lasso的一种方法。

相比于常规的梯度下降（每个梯度都是各个维度的线性组合），坐标梯度下降法只沿着平行于坐标轴进行迭代。其步骤大致如下：

初始化一个点
对这个点的四周（平行于坐标轴的方向）求偏导（这个不会收到L1范数范数的影响）
选择一个偏导最大的方向，并沿着其反方向下降。（这和梯度下降几乎一样）
重复2、3步骤直到达到极小值或最小值（当然实际过程中也有可能是别的什么点）

3.2最小角回归LARs

最小角回归是综合了“前向选择”和“前向梯度”的一种优化算法，它通过两种方式减少了迭代次数.。（它也是sklearn中给出的方法）

在每个方向上只迭代一次（通过设置条件而终止当前的迭代）
对不同特征进行线性组合

那么它做了一件什么事，终止迭代的步骤又是啥

首先，它根据维度划分出n个向量（n个维度），其中每个维度的向量由不同样本（共m个）在该维度的值组成
其次，每一步迭代，它计算不同维度的向量与标签Y的夹角（cos），并选择最小的一个作为当前迭代的方向。
当前迭代的终止条件是：遇到另一个向量与现在的方向到残差的夹角相等。
然后我们沿着这两个向量的“角平分线”继续前进（迭代），知道遇到另一个向量到残差的夹角与当前方向到残差的距离相等。

具体的推导和部分可视化大家可以参照刘建平大佬写的博客

3.3近端梯度下降

近端梯度下降(Proximal Gradient Descent)是西瓜书里给出的对Lasso的求解，里面用到了泰勒的二级展开和部分软阈值函数。

我们的目标函数分为可微的“损失函数”和不可微的“正则项”。

在近端梯度下降中，我们对不可微的“正则项”对处理反而很简单，那就是用软阈值函数来表示它的导数。（在 $l_1$ 范数上的体现就是去绝对值然后分段求导，是不是非常的简单粗暴）

然而对于“损失函数”，常规情况下，我们的做法是对其求一阶导，然后将导数和学习率的乘积作为我们每次迭代的方向和步长。

但是在这里，我们通过泰勒公式对“损失函数”进行二阶展开，并用近端算子将二阶导近似为常数（建议：如果不是数学系的没必要深究近端算子的含义，只需要知道它是个不等式），所以最后我们的“损失函数”可以整理成为一个二次函数。

在该二次函数（“损失函数”在当前点 $x_k$ 的附近的近似值）中，其最小值，可视为下次迭代的目标 $x_{k+1}$ 。当然啦，在这里，我们先将其记为 $z_{k+1}$ ，毕竟它只是个中间变量。整个目标函数的迭代目标应该 $x_{k+1}$ 是将 $z_{k+1}$ 带入到我们之前说的“软阈值函数”所得的函数值。