转自:http://blog.csdn.net/slade_sha/article/details/53164905
先看一波过拟合:
图中,红色的线存在明显的过拟合,绿色的线才是合理的拟合曲线,为了避免过拟合,我们可以引入正则化。
下面可以利用正则化来解决曲线拟合过程中的过拟合发生,存在均方根误差也叫标准误差,即为√[∑di^2/n]=Re,n为测量次数;di为一组测量值与真值的偏差。
实际考虑回归的过程中,我们需要考虑到误差项,
这个和简单的线性回归的公式相似,而在正则化下来优化过拟合这件事情的时候,会加入一个约束条件,也就是惩罚函数:
这边这个惩罚函数有多种形式,比较常用的有l1,l2,大概有如下几种:
讲一下比较常用的两种情况,q=1和q=2的情况:
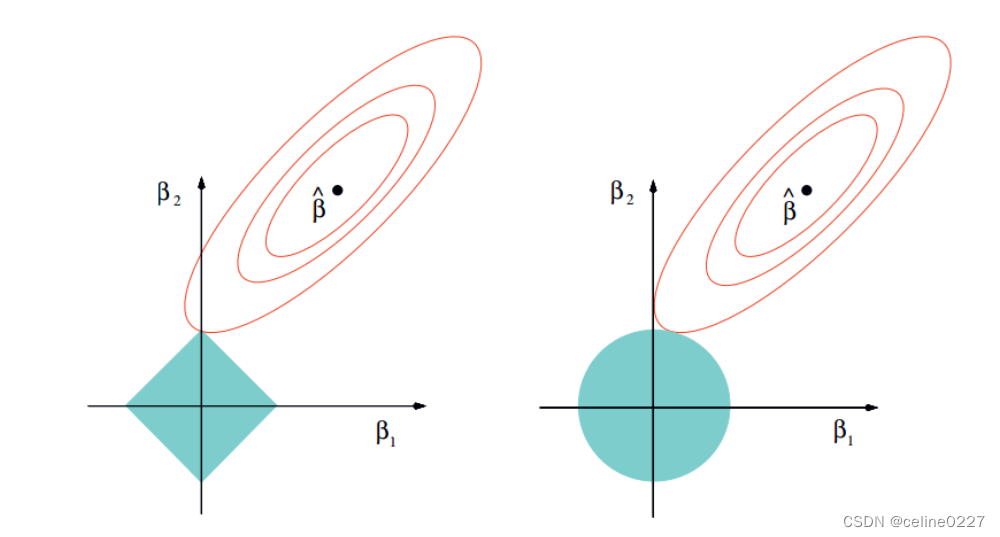
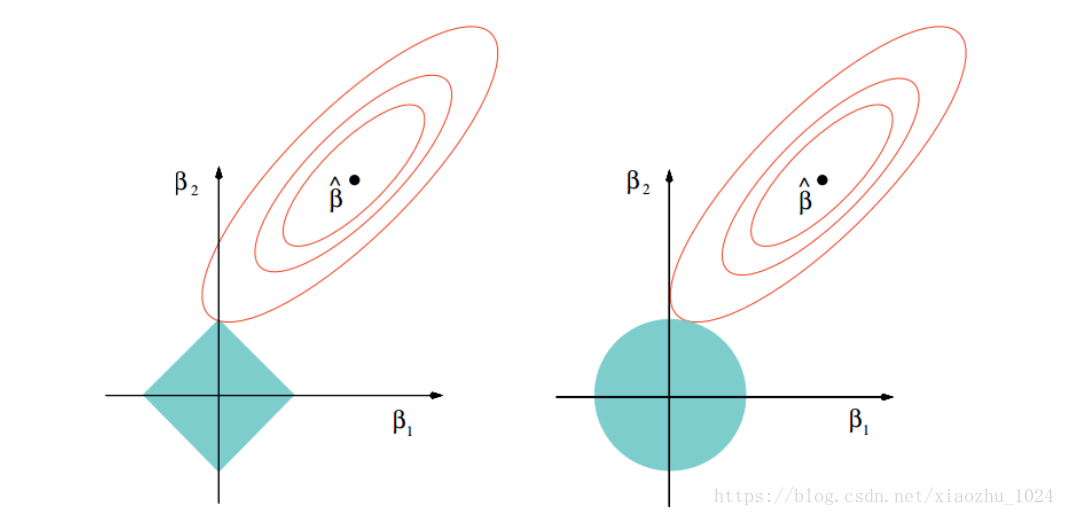
q=1,也就是今天想讲的lasso回归,为什么lasso可以控制过拟合呢,因为在数据训练的过程中,可能有几百个,或者几千个变量,再过多的变量衡量目标函数的因变量的时候,可能造成结果的过度解释,而通过q=1下的惩罚函数来限制变量个数的情况,可以优先筛选掉一些不是特别重要的变量,见下图:
作图只要不是特殊情况下与正方形的边相切,一定是与某个顶点优先相交,那必然存在横纵坐标轴中的一个系数为0,起到对变量的筛选的作用。
q=2的时候,其实就可以看作是上面这个蓝色的圆,在这个圆的限制下,点可以是圆上的任意一点,所以q=2的时候也叫做岭回归,岭回归是起不到压缩变量的作用的,在这个图里也是可以看出来的。
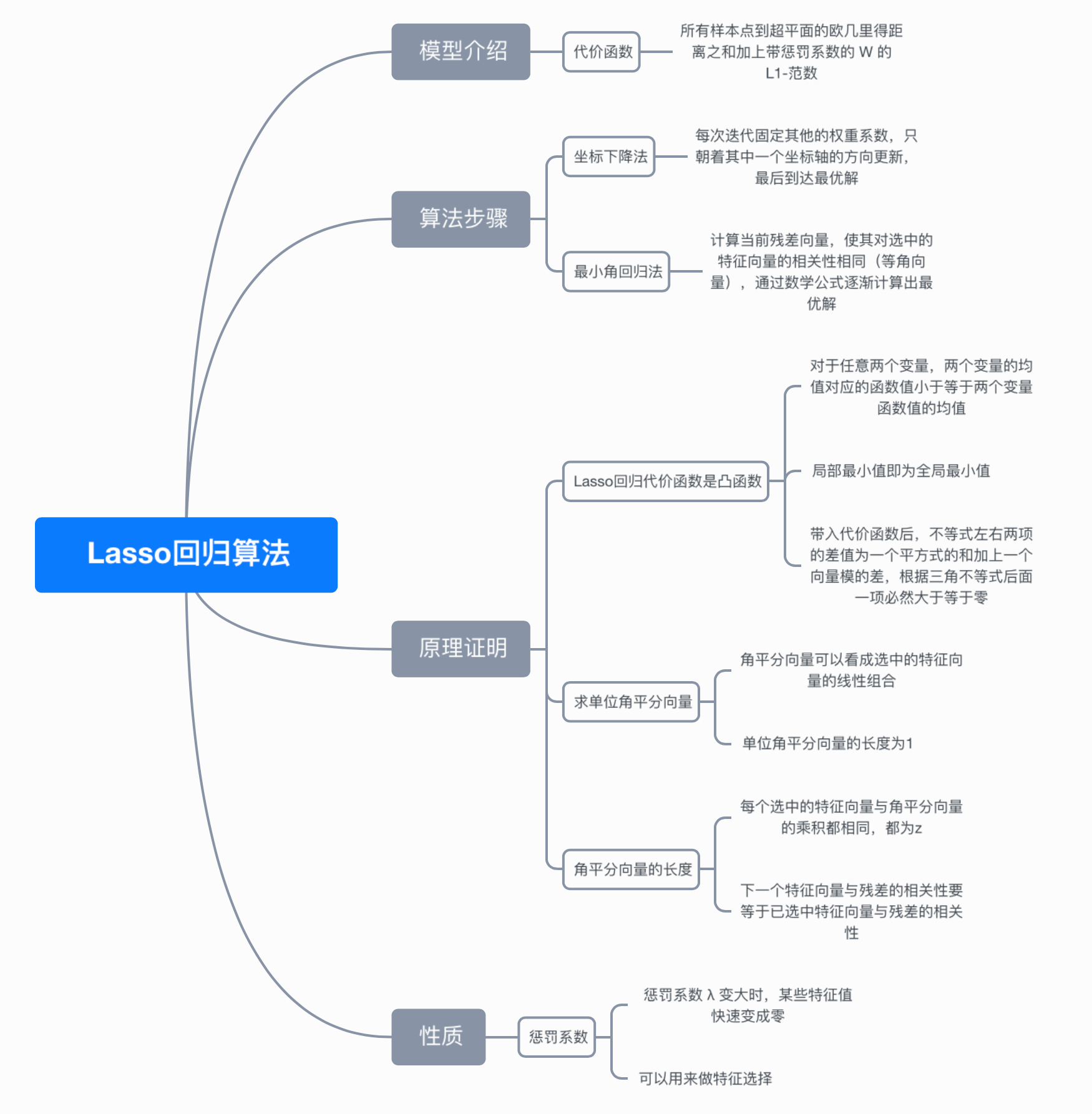
lasso回归:
lasso回归的特色就是在建立广义线型模型的时候,这里广义线型模型包含一维连续因变量、多维连续因变量、非负次数因变量、二元离散因变量、多元离散因变,除此之外,无论因变量是连续的还是离散的,lasso都能处理,总的来说,lasso对于数据的要求是极其低的,所以应用程度较广;除此之外,lasso还能够对变量进行筛选和对模型的复杂程度进行降低。这里的变量筛选是指不把所有的变量都放入模型中进行拟合,而是有选择的把变量放入模型从而得到更好的性能参数。 复杂度调整是指通过一系列参数控制模型的复杂度,从而避免过度拟合(Overfitting)。 对于线性模型来说,复杂度与模型的变量数有直接关系,变量数越多,模型复杂度就越高。 更多的变量在拟合时往往可以给出一个看似更好的模型,但是同时也面临过度拟合的危险。
lasso的复杂程度由λ来控制,λ越大对变量较多的线性模型的惩罚力度就越大,从而最终获得一个变量较少的模型。除此之外,另一个参数α来控制应对高相关性(highly correlated)数据时模型的性状。 LASSO回归α=1,Ridge回归α=0,这就对应了惩罚函数的形式和目的。我们可以通过尝试若干次不同值下的λ,来选取最优λ下的参数,还可以结合CV选择最优秀的模型。
##读取数据
setwd("~/Desktop")
library(glmnet)
train_origin<-read.table('trian.txt',header = T,fill = T)
test_origin<-read.table('test.txt',header = T,fill = T)
train_test1<-train_origin
train_test1<-train_test1[,-9]
train_test1$tag<-as.factor(train_test1$tag)
train_test1$risk_level<-as.factor(train_test1$risk_level)
x<-train_test1[,3:11]
y<-train_test1[,2]
## one hot encoding
x1<-model.matrix(~., x)
通常数据中会存在离散点,而lasso在R里面是通过数值矩阵来做输入的,所以需要对原数据做一步预处理,不然这边会抛错误;除此之外,如果数据之间差别的数量级较大,还需要进行标准化,R里面也是可以进行处理的,这边就不赘述了,glmnet()函数中添加参数standardize = TRUE来实现,scale()函数也可以实现,自行选择即可。
##模型训练
model = glmnet(x1, y, family="binomial", nlambda=50, alpha=1)
family里面是指选择函数的类型:
| family | explation |
| gaussian | univariate |
| mgaussian | multivariate |
| poisson | count |
| binomial | binary |
| multinomial | category |
lambda是指随机选择λ,做lambda个模型;alpha是上述讲到的α,选择惩罚函数,正常情况下,1是lasso,0是岭回归
这边模型拓展可以交叉检验一下,有内置的函数:
cvmodel = cv.glmnet(x1, y, family = "binomial", type.measure = "class",nfolds=10)
这边会多出来一个type.measure,这个type.measure是指期望最小化的目标参量是什么,换句话说,就是衡量这个模型的指标函数是啥:
| type.measure | details |
| deviance | -2倍的Log-likelihood |
| mse | mean squred error |
| mae | mean absolute error |
| class | missclassification error |
| auc | area under the ROC curve |
比较常用的是auc,这个就是现在比较主流的衡量一个模型好坏的roc所衍生出来的一个值;我们这边用的是class,也就是模型错误分配的概率,结合我这次业务开发的实际业务场景,这个更合适一点;nfolds是指folds数目,也可以通过foldid数来控制每个fold里面的数据数量。
对于glmnet,可以通过plot(model)来观察每个自变量的变化轨迹,cv.glmnet可以通过plot(cvmodel)
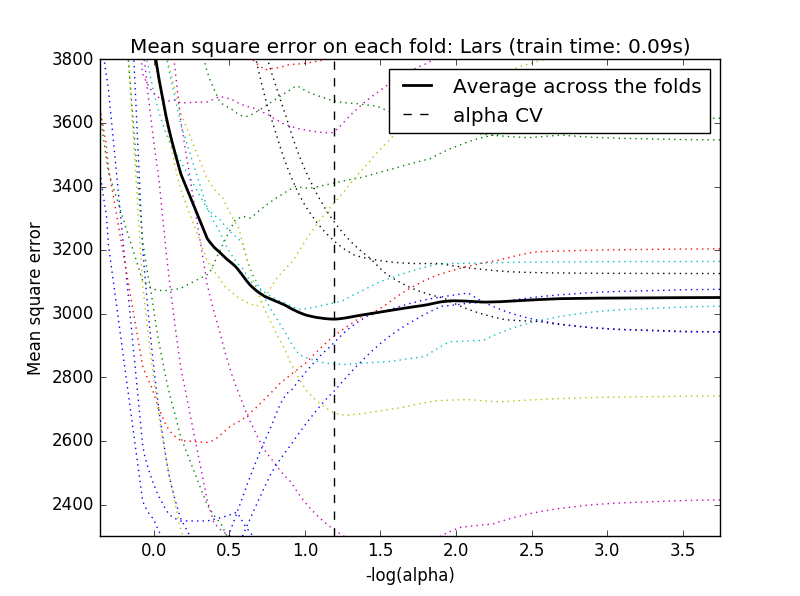
举个plot(cvmodel)的例子:
可以通过c(cvfit$lambda.min, cvfit$lambda.1se)来看在所有的λ值中,得到最小目标函数type.measure均值的cvfit$lambda.min,以及其所对应的λ值cvfit$lambda.1se。
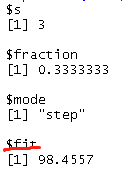
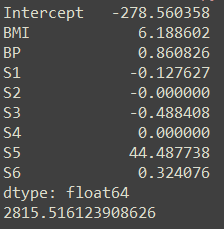
我们可以print(model),在实际的选择模型中λ值的过程里,存在三个指标:df:自由度, %Dev:残差被解释的占比,也就是模型的好坏程度,Lambda也就是λ值所对应的值,然后我们可以通过coef(fit, s=c(fit$lambda[35],0.002))得出当时模型所对应的系数。
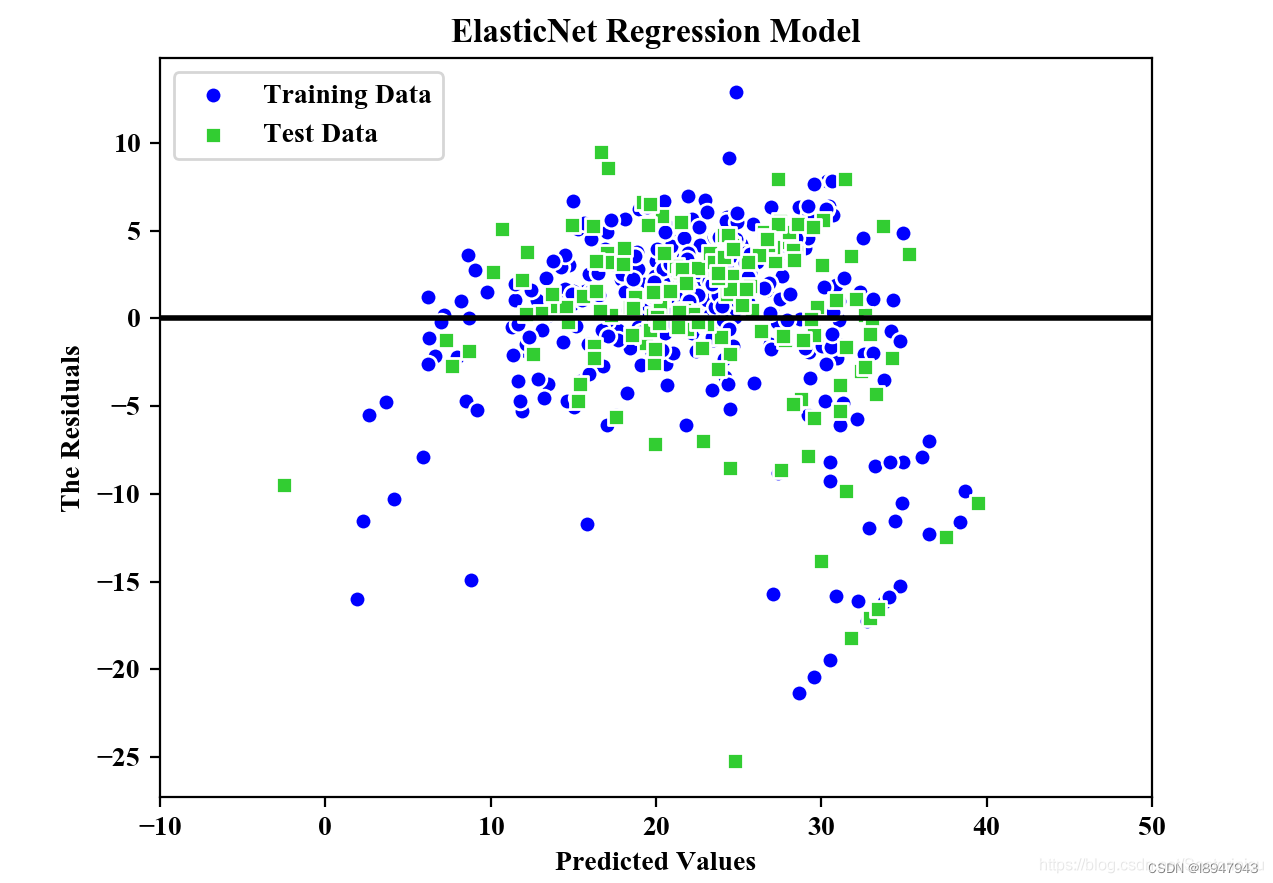
最后,讲一下elastic net
elastic net融合了l1范数和l2范数两种正则化的方法,上面的岭回归和lasso回归都可以看做它的特例:
elastic net对于p远大于n,或者严重的多重共线性情况有明显的效果,很好理解,当alpha接近1时,elastic net表现很接近lasso,一般来说,elastic net是岭回归和lasso的很好的折中,当alpha从0变化到1,目标函数的稀疏解(部分变量的系数为0)也从0单调增加到lasso的稀疏解。