机器学习--岭回归和Lasso回归

article/2025/9/28 21:17:56

任何数据都存在噪声和多重共线性
如何解决多重共线性？
1.算法角度（正则化）
2.数据角度（最有效果）

岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合（数据间高度线性相关）以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的，这两种回归均通过在损失函数中引入正则化项来达到目的，具体三者的损失函数对比见下图：
在这里插入图片描述
其中λ称为正则化参数，如果λ选取过大，会把所有参数θ均最小化，造成欠拟合，如果λ选取过小，会导致对过拟合问题解决不当，因此λ的选取是一个技术活。

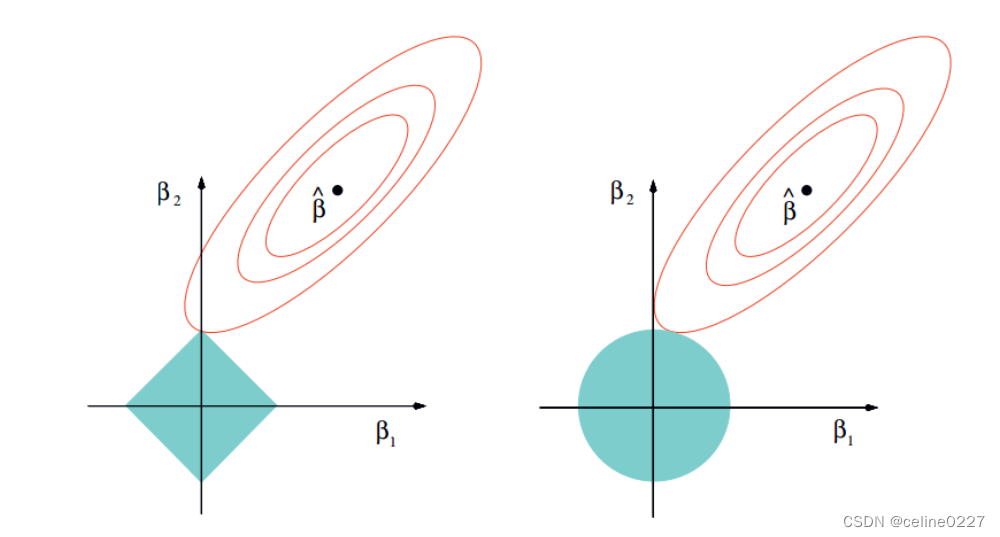
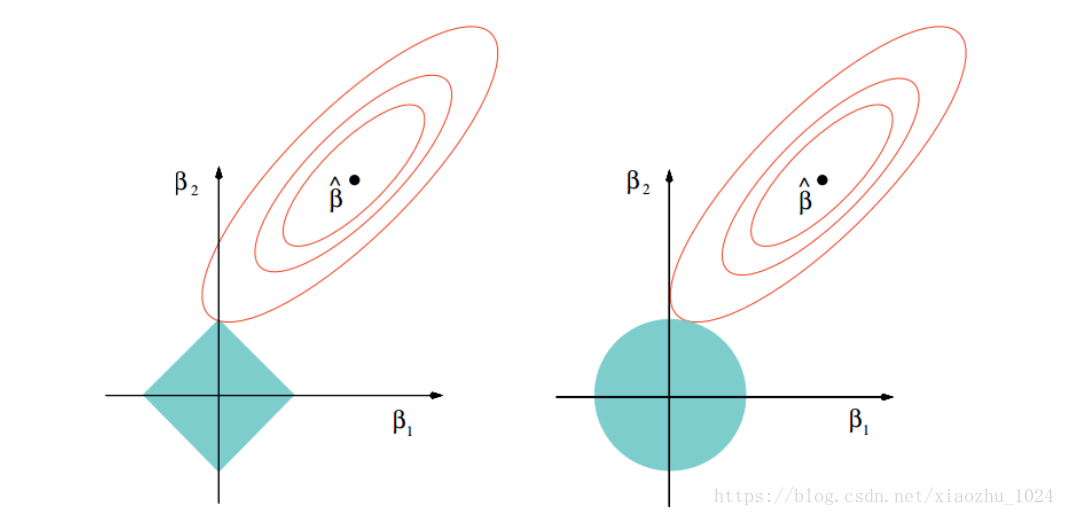
岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项，Lasso回归引入的是L1范数惩罚项，Lasso回归能够使得损失函数中的许多θ均变成0，这点要优于岭回归，因为岭回归是要所有的θ均存在的，这样计算量Lasso回归将远远小于岭回归。

一、岭回归

1.1 回归系数计算公式：

在这里插入图片描述
其中λ为正则系数，I为单位矩阵。

1.2 优点

缩减方法可以去掉不重要的参数，因此能更好地理解数据。此外，与简单的线性回归相比，缩减法能取得更好的预测效果。.岭回归作为一种缩减算法可以判断哪些特征重要或者不重要，有点类似于降维的效果

岭回归是加了二阶正则项的最小二乘，主要适用于过拟合严重或各变量之间存在多重共线性的时候，岭回归是有bias的，这里的bias是为了让variance更小。

缩减算法可以看作是对一个模型增加偏差的同时减少方差

1.3 应用场景

岭回归可以解决特征数量比样本量多的问题
变量间存在共线性（最小二乘回归得到的系数不稳定，方差很大）
应用场景就是处理高度相关的数据

1.4 简单应用

对糖尿病数据集进行岭回归建模

from pandas import Series,DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inlinefrom sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_splitdiabetes = load_diabetes()
train = diabetes.data
target = diabetes.target
feature_names = diabetes.feature_namesX_train,X_test,y_train,y_test = train_test_split(train,target,test_size=0.2)rideg = Ridge(alpha=1.0)
rideg.fit(X_train,y_train)# 获取训练好模型的w参数
rideg.coef_# 对w参数绘制图形，通过w的大小可以进行特征选择
sns.set()
importances = Series(data=np.abs(rideg.coef_),index=feature_names).sort_values(ascending=False)
importances.plot(kind='bar')
plt.xticks(rotation=0)
plt.show()# 由图像我们选择前七个特征
importancesm_cols = ['sex','bmi','bp','s3','s4','s6','s5']
datasets = DataFrame(data=train,columns=feature_names)
X = datasets[importancesm_cols]
y = targetX_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
rideg = Ridge(alpha=1.0)
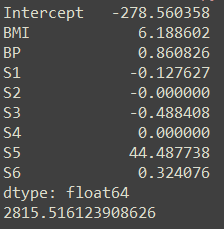
rideg.fit(X_train,y_train)from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,rideg.predict(X_test))

图像如下：
在这里插入图片描述

二、Lasso回归

与岭回归相似的是，LASSO 回归同样是通过添加正则项来改进普通最小二乘法，不过这里添加的是 L1 正则项。即：
在这里插入图片描述

L1：L1正则化最大的特点是能稀疏矩阵，进行庞大特征数量下的特征选择
L1是模型各个参数的绝对值之和

L2：L2正则能够有效的防止模型过拟合，解决非满秩下求逆困难的问题
L2是模型各个参数的平方和的开方值。

2.1 简单应用

import numpy as np
from scipy.linalg import hilbert
from sklearn.linear_model import Lasso
import matplotlib.pyplot as plt
%matplotlib inline"""使用LASSO 回归拟合并绘图
"""
from sklearn.linear_model import Lassox = hilbert(10)
w = np.random.randint(2,10,10) # 随机生成 w 系数
y_temp = np.matrix(x) * np.matrix(w).T # 计算 y 值
y = np.array(y_temp.T)[0] #将 y 值转换成 1 维行向量  相当于给矩阵创建一个真实值
alphas = np.linspace(-2,2,10)
lasso_coefs = []
for a in alphas:lasso = Lasso(alpha=a,fit_intercept=False)lasso.fit(x,y)lasso_coefs.append(lasso.coef_)plt.plot(alphas,lasso_coefs) # 绘制不同alpha下的 w 拟合值
plt.xlabel('alpha')
plt.ylabel('w')
plt.title('Lasso Regression')
plt.scatter(np.linspace(0,0,10),parameters[0]) # 普通最小二乘法的 w 放入图中plt.show()