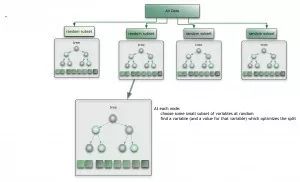
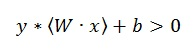Lasso回归

article/2025/9/28 22:22:57

维数灾难

高维数据

何谓高维数据？高维数据指数据的维度很高，甚至远大于样本量的个数。高维数据的明显的表现是：在空间中数据是非常稀疏的，与空间的维数相比样本量总是显得非常少。
在分析高维数据过程中碰到最大的问题就是维数的膨胀，也就是通常所说的“维数灾难”问题。研究表明，随着维数的增长，分析所需的空间样本数会呈指数增长。
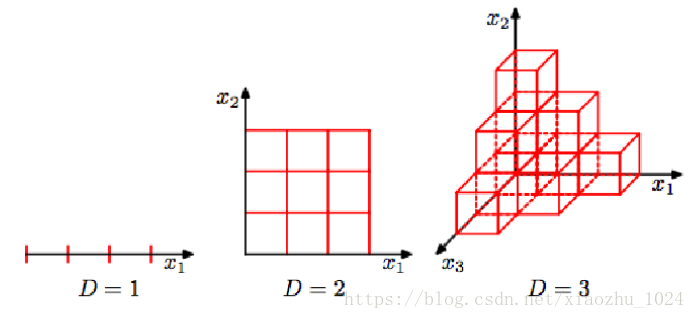
如下所示，当数据空间维度由1增加为3，最明显的变化是其所需样本增加；换言之，当样本量确定时，样本密度将会降低，从而样本呈稀疏状态。假设样本量n=12,单个维度宽度为3，那在一维空间下，样本密度为12/3=4，在二维空间下，样本分布空间大小为3*3，则样本密度为12/9=1.33，在三维空间下样本密度为12/27=0.44。
设想一下，当数据空间为更高维时，X=[ $x_1$ , $x_2$ ,…., $x_n$ ]会怎么样？
样本数据维度由一维增加为三维

需要更多的样本，样本随着数据维度的增加呈指数型增长；
数据变得更稀疏，导致数据灾难；
在高维数据空间，预测将变得不再容易；
导致模型过拟合。

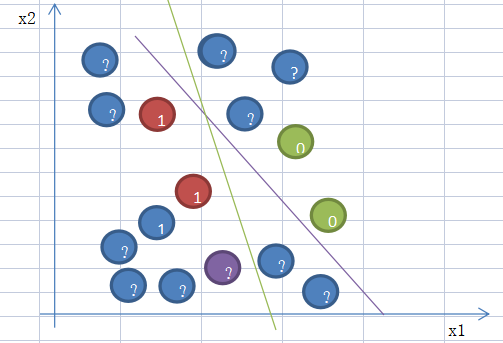
维数灾难在分类问题中的体现

具体例子可以参考机器学习:分类问题中的“维数灾难”

数据降维

对于高维数据，维数灾难所带来的过拟合问题，其解决思路是：1）增加样本量；2）减少样本特征，而对于现实情况，会存在所能获取到的样本数据量有限的情况，甚至远小于数据维度，即：d>>n。如证券市场交易数据、多媒体图形图像视频数据、航天航空采集数据、生物特征数据等。
主成分分析作为一种数据降维方法，其出发点是通过整合原本的单一变量来得到一组新的综合变量，综合变量所代表的意义丰富且变量间互不相关，综合变量包含了原变量大部分的信息，这些综合变量称为主成分。主成分分析是在保留所有原变量的基础上，通过原变量的线性组合得到主成分，选取少数主成分就可保留原变量的绝大部分信息，这样就可用这几个主成分来代替原变量，从而达到降维的目的。

但是，主成分分析法只适用于数据空间维度小于样本量的情况，当数据空间维度很高时，将不再适用。

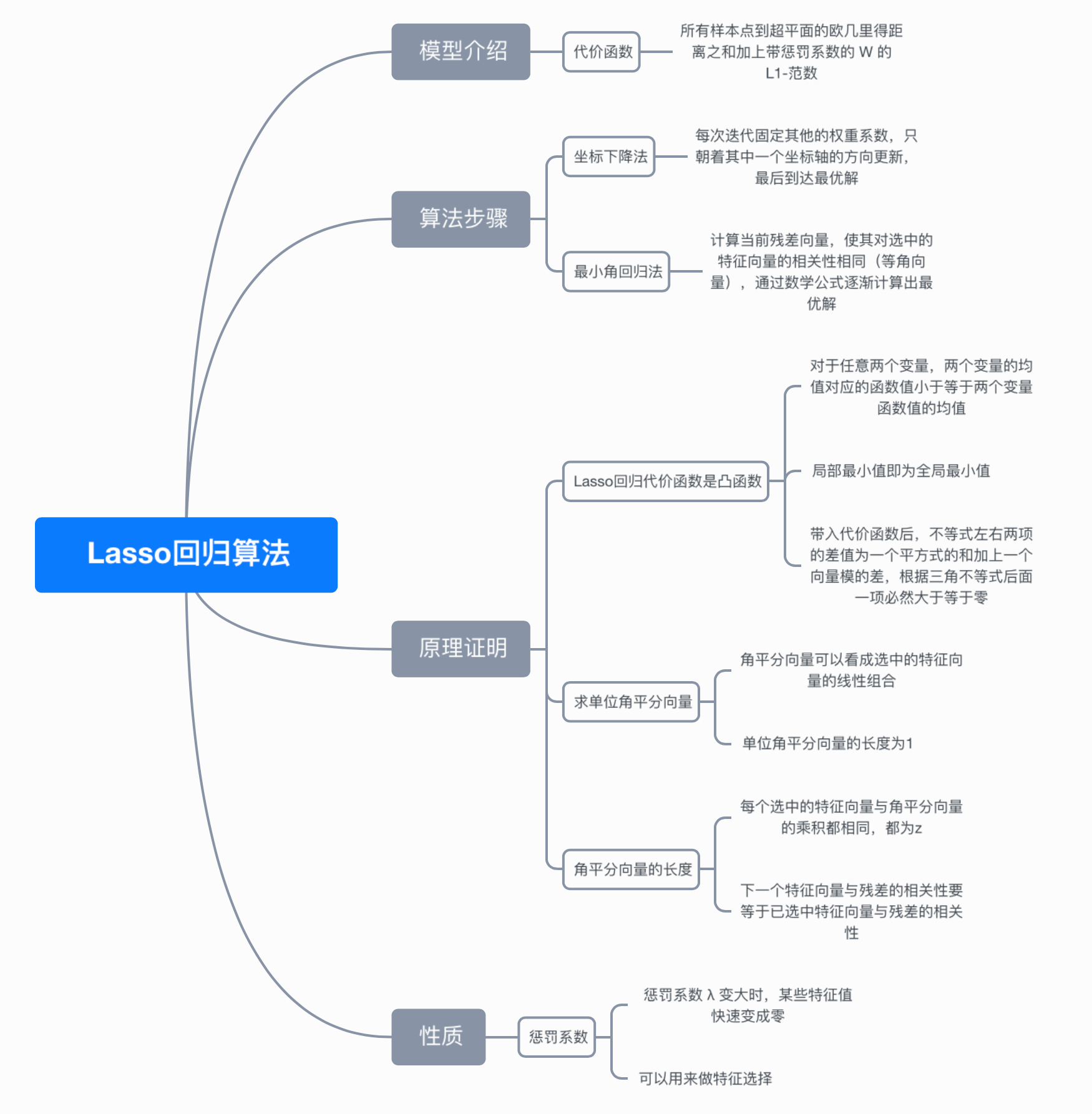
Lasso是另一种数据降维方法，该方法不仅适用于线性情况，也适用于非线性情况。Lasso是基于惩罚方法对样本数据进行变量选择，通过对原本的系数进行压缩，将原本很小的系数直接压缩至0，从而将这部分系数所对应的变量视为非显著性变量，将不显著的变量直接舍弃。

Lasso回归

普通线性模型

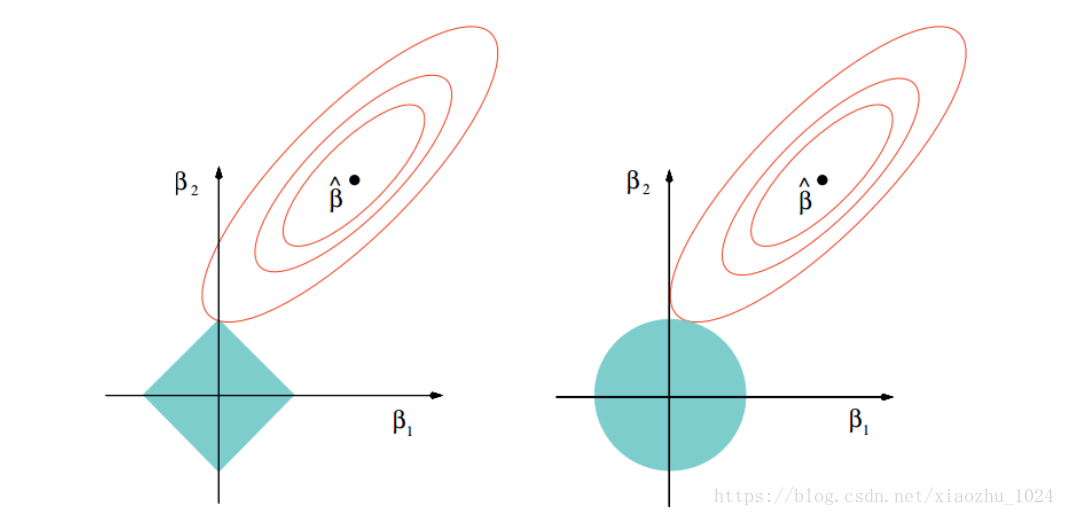
这里写图片描述

惩罚方法

这里写图片描述

Lasso方法

这里写图片描述

Ridge方法

这里写图片描述

图形比较

这里写图片描述
以二维数据空间为例，说明lasso和Ridge两种方法的差异，左图对应于Lasso方法，右图对应于Ridge方法。
如上图所示，两个图是对应于两种方法的等高线与约束域。红色的椭圆代表的是随着 $\lambda$ 的变化所得到的残差平方和， $\widehat{\beta}$ 为椭圆的中心点，为对应普通线性模型的最小二乘估计。左右两个图的区别在于约束域，即对应的蓝色区域。
等高线和约束域的切点就是目标函数的最优解，Ridge方法对应的约束域是圆，其切点只会存在于圆周上，不会与坐标轴相切，则在任一维度上的取值都不为0，因此没有稀疏；对于Lasso方法,其约束域是正方形，会存在与坐标轴的切点，使得部分维度特征权重为0，因此很容易产生稀疏的结果。
所以，Lasso方法可以达到变量选择的效果，将不显著的变量系数压缩至0，而Ridge方法虽然也对原本的系数进行了一定程度的压缩，但是任一系数都不会压缩至0，最终模型保留了所有的变量。

代码块

#加载模块
import numpy as np
import matplotlib.pyplot as plt
import time
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score
from sklearn.linear_model import LassoCV
from sklearn.model_selection import train_test_split# 生成稀疏样本数据
np.random.seed(int(time.time()))# 生成系数数据，样本为50个，参数为300维
n_samples, n_features = 50, 300# 模拟服从正态分布的样本数据
X = np.random.randn(n_samples, n_features)# 每个变量对应的系数
coef = 2 * np.random.randn(n_features)# 变量的下标
inds = np.arange(n_features)# 变量下标随机排列
np.random.shuffle(inds)# 仅仅保留10个变量的系数，其他系数全部设置为0,生成稀疏参数
coef[inds[10:]] = 0# 得到目标值，y
y = np.dot(X, coef)# 为y添加噪声
y += 0.01 * np.random.normal((n_samples,))# 将数据分为训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=14)# LassoCV: 基于坐标下降法的Lasso交叉验证,这里使用20折交叉验证法选择最佳alpha
print("使用坐标轴下降法计算参数正则化路径:")
model = LassoCV(cv=20).fit(X, y)# 最终alpha的结果，因为有的alpha实在是太小了，所以使用负对数形式表示
m_log_alphas = -np.log10(model.alphas_)"""
由于这里使用的是20折交叉验证,所以model.mse_path_有20列；
model.mse_path_中每一列，是对应交叉验证，在alpha选择不同值的时候，其对应的均方误差（mean square error）；
模型最终选择的alpha是所有交叉验证结果的平均值中，最小的那个平均的均方误差对应的alpha。
"""# 作出交叉验证不同的alpha取值对应的MSE的轨迹图plt.figure()
ymin, ymax = 500, 1500
plt.plot(m_log_alphas, model.mse_path_, ':')
plt.plot(m_log_alphas, model.mse_path_.mean(axis=-1), 'k',label='Average across the folds', linewidth=2)
plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k',label='alpha: CV estimate')plt.legend()
plt.xlabel('-log(alpha)')
plt.ylabel('Mean square error')
plt.title('Mean square error on each fold: coordinate descent')
plt.axis('tight')
plt.ylim(ymin, ymax)# Lasso 回归的参数
alpha = model.alpha_
lasso = Lasso(max_iter=10000, alpha=alpha)# 基于训练数据，得到的模型的测试结果,这里使用的是坐标轴下降算法（coordinate descent）
y_pred_lasso = lasso.fit(X_train, y_train).predict(X_test)# 这里是R2可决系数（coefficient of determination）
# 回归平方和（RSS）在总变差（TSS）中所占的比重称为可决系数
# 可决系数可以作为综合度量回归模型对样本观测值拟合优度的度量指标。
# 可决系数越大，说明在总变差中由模型作出了解释的部分占的比重越大，模型拟合优度越好。
# 反之可决系数小，说明模型对样本观测值的拟合程度越差。
# R2可决系数最好的效果是1。
r2_score_lasso = r2_score(y_test, y_pred_lasso)print("测试集上的R2可决系数 :{:2f}" .format(r2_score_lasso))plt.plot(lasso.coef_, label='Lasso coefficients')
plt.plot(coef, '--', label='original coefficients')
plt.legend(loc='best')plt.show()