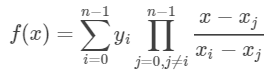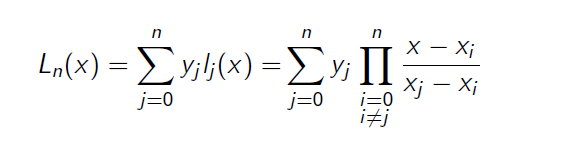整理一下数值分析的笔记~
目录:1. 误差
2. 多项式插值与样条插值(THIS)
3. 函数逼近
4. 数值积分与数值微分
5. 线性方程组的直接解法
6. 线性方程组的迭代解法
7. 非线性方程求根
8. 特征值和特征向量的计算
9. 常微分方程初值问题的数值解
1. 拉格朗日基函数
定义. 设 l k ( x ) l_k(x) lk(x)是n次多项式,在插值节点 x 0 , x 1 , . . . , x n x_0,x_1,...,x_n x0,x1,...,xn上满足:
l k ( x j ) = { 1 , j = k 0 , j ≠ k l_k(x_j)=\begin{cases} 1,&j=k\\ 0,&j \neq k \end{cases} lk(xj)={1,0,j=kj̸=k
则称 l k ( x ) l_k(x) lk(x)为节点 x 0 , x 1 , . . . , x n x_0,x_1,...,x_n x0,x1,...,xn上的拉格朗日插值基函数。
n=1 → \rarr → 线性插值
问题定义:给定区间 [ x k , x k + 1 ] [x_k,x_{k+1}] [xk,xk+1]及端点函数值: y k = f ( x k ) , y k + 1 = f ( x k + 1 ) y_k=f(x_k),y_{k+1}=f(x_{k+1}) yk=f(xk),yk+1=f(xk+1),求线性插值多项式 L 1 ( x ) L_1(x) L1(x),使其满足 L 1 ( x k ) = y k , L 1 ( x k + 1 ) = y k + 1 L_1(x_k)=y_k,L_1(x_{k+1})=y_{k+1} L1(xk)=yk,L1(xk+1)=yk+1。
不难看出几何上就是通过两点的直线,两点式有: L 1 ( x ) = x k + 1 − x x k + 1 − x k y k + x − x k x k + 1 − x k y k + 1 L_1(x)=\frac{x_{k+1}-x}{x_{k+1}-x_k}y_k+\frac{x-x_k}{x_{k+1}-x_k}y_{k+1} L1(x)=xk+1−xkxk+1−xyk+xk+1−xkx−xkyk+1
即 L 1 ( x ) L_1(x) L1(x)是两个线性函数 l k ( x ) = x k + 1 − x x k + 1 − x k , l k + 1 ( x ) = x − x k x k + 1 − x k l_k(x)=\frac{x_{k+1}-x}{x_{k+1}-x_k},l_{k+1}(x)=\frac{x-x_k}{x_{k+1}-x_k} lk(x)=xk+1−xkxk+1−x,lk+1(x)=xk+1−xkx−xk
的线性组合,系数分别是 y k 和 y k + 1 y_k和y_{k+1} yk和yk+1,即:
L 1 ( x ) = y k l k ( x ) + y k + 1 l k + 1 ( x ) L_1(x)=y_kl_k(x)+y_{k+1}l_{k+1}(x) L1(x)=yklk(x)+yk+1lk+1(x)
显然:
l k ( x k ) = 1 , l k ( x k + 1 ) = 0 l k + 1 ( x k ) = 0 , l k + 1 ( x k + 1 ) = 1 l_k(x_k)=1,l_k(x_{k+1})=0\\ l_{k+1}(x_k)=0,l_{k+1}(x_{k+1})=1 lk(xk)=1,lk(xk+1)=0lk+1(xk)=0,lk+1(xk+1)=1
称 l k ( x ) 和 l k + 1 ( x ) l_k(x)和l_{k+1}(x) lk(x)和lk+1(x)为线性插值基函数。
n=2 → \rarr → 抛物插值
同理,假定插值节点为 x k − 1 , x k , x k + 1 x_{k-1},x_k,x_{k+1} xk−1,xk,xk+1,求二次插值多项式 L 2 ( x ) L_2(x) L2(x)使其满足 L 2 ( x j ) = y j , ( j = k − 1 , k , k + 1 ) L_2(x_j)=y_j,(j=k-1,k,k+1) L2(xj)=yj,(j=k−1,k,k+1),几何上其为通过三点 ( x k − 1 , y k − 1 ) , ( x k , y k ) , ( x k + 1 , y k + 1 ) (x_{k-1},y_{k-1}),(x_k,y_k),(x_{k+1},y_{k+1}) (xk−1,yk−1),(xk,yk),(xk+1,yk+1)的抛物线,用基函数的方法求 L 2 ( x ) L_2(x) L2(x)的表达式,此时基函数 l k − 1 ( x ) , l k ( x ) , l k + 1 ( x ) l_{k-1}(x),l_k(x),l_{k+1}(x) lk−1(x),lk(x),lk+1(x)是二次函数,且在节点上满足条件:
l k − 1 ( x k − 1 ) = 1 , l k − 1 ( x k ) = 0 , l k − 1 ( x k + 1 ) = 0 l k ( x k − 1 ) = 0 , l k ( x k ) = 1 , l k ( x k + 1 ) = 0 l k + 1 ( x k − 1 ) = 0 , l k + 1 ( x k ) = 0 , l k + 1 ( x k + 1 ) = 1 l_{k-1}(x_{k-1})=1,l_{k-1}(x_{k})=0,l_{k-1}(x_{k+1})=0\\ l_k(x_{k-1})=0,l_k(x_k)=1,l_k(x_{k+1})=0\\ l_{k+1}(x_{k-1})=0,l_{k+1}(x_k)=0,l_{k+1}(x_{k+1})=1 lk−1(xk−1)=1,lk−1(xk)=0,lk−1(xk+1)=0lk(xk−1)=0,lk(xk)=1,lk(xk+1)=0lk+1(xk−1)=0,lk+1(xk)=0,lk+1(xk+1)=1
以 l k l_{k} lk为例,由上面的式子可以知道它有两个零点 x k − 1 , x k + 1 x_{k-1},x_{k+1} xk−1,xk+1,有 l k ( x ) = A ( x − x k − 1 ) ( x − x k + 1 ) l_k(x)=A(x-x_{k-1})(x-x_{k+1}) lk(x)=A(x−xk−1)(x−xk+1),其中A为待定系数,根据 l k ( x k ) = 1 l_{k}(x_{k})=1 lk(xk)=1定出:
A = 1 ( x k − x k − 1 ) ( x k − x k + 1 ) A=\frac{1}{(x_k-x_{k-1})(x_k-x_{k+1})} A=(xk−xk−1)(xk−xk+1)1
于是有:
l k ( x ) = ( x − x k − 1 ) ( x − x k + 1 ) ( x k − x k − 1 ) ( x k − x k + 1 ) l_k(x)=\frac{(x-x_{k-1})(x-x_{k+1})}{(x_k-x_{k-1})(x_k-x_{k+1})} lk(x)=(xk−xk−1)(xk−xk+1)(x−xk−1)(x−xk+1)
同理:
l k − 1 ( x ) = ( x − x k ) ( x − x k + 1 ) ( x k − 1 − x k ) ( x k − 1 − x k + 1 ) l k + 1 ( x ) = ( x − x k − 1 ) ( x − x k ) ( x k + 1 − x k − 1 ) ( x k + 1 − x k ) l_{k-1}(x)=\frac{(x-x_{k})(x-x_{k+1})}{(x_{k-1}-x_k)(x_{k-1}-x_{k+1})}\\ l_{k+1}(x)=\frac{(x-x_{k-1})(x-x_{k})}{(x_{k+1}-x_{k-1})(x_{k+1}-x_{k})} lk−1(x)=(xk−1−xk)(xk−1−xk+1)(x−xk)(x−xk+1)lk+1(x)=(xk+1−xk−1)(xk+1−xk)(x−xk−1)(x−xk)
可得二次插值多项式:
L 2 ( x ) = y k − 1 l k − 1 ( x ) + y k l k ( x ) + y k + 1 l k + 1 ( x ) L_2(x)=y_{k-1}l_{k-1}(x)+y_{k}l_{k}(x)+y_{k+1}l_{k+1}(x) L2(x)=yk−1lk−1(x)+yklk(x)+yk+1lk+1(x)
2. 拉格朗日插值多项式
推广至一般情形,构造通过n+1个节点的n次插值多项式 L n ( x ) L_n(x) Ln(x).根据插值定义有: L n ( x j ) = y j , ( j = 0 , 1 , . . . , n ) L_n(x_j)=y_j,(j=0,1,...,n) Ln(xj)=yj,(j=0,1,...,n)。为此先定义n次插值基函数:
定义1 若n次多项式 L j ( x ) ( j = 0 , 1 , 2 , . . . , n ) L_j(x)(j=0,1,2,...,n) Lj(x)(j=0,1,2,...,n)在n+1个节点 x 0 < x 1 < . . . < x n x_0<x_1<...<x_n x0<x1<...<xn上满足条件:
l k ( x j ) = { 1 , j = k 0 , j ≠ k , ( j , k = 0 , 1 , . . . , n ) l_k(x_j)=\begin{cases} 1,&j=k\\ 0,&j \neq k \end{cases},(j,k=0,1,...,n) lk(xj)={1,0,j=kj̸=k,(j,k=0,1,...,n)
就称这n+1个n次多项式 l 0 ( x ) , l 1 ( x ) , . . . , l n ( x ) l_0(x),l_1(x),...,l_n(x) l0(x),l1(x),...,ln(x)为节点 x 0 , x 1 , . . . , x n x_0,x_1,...,x_n x0,x1,...,xn上的n次插值基函数,类似地:
l k ( x ) = ( x − x 0 ) . . . ( x − x k − 1 ) ( x − x k + 1 ) . . . ( x − x n ) ( x k − x 0 ) . . . ( x k − x k − 1 ) ( x k − x k + 1 ) . . . ( x k − x n ) l_k(x)=\frac{(x-x_0)...(x-x_{k-1})(x-x_{k+1})...(x-x_n)}{(x_k-x_0)...(x_k-x_{k-1})(x_k-x_{k+1})...(x_k-x_n)} lk(x)=(xk−x0)...(xk−xk−1)(xk−xk+1)...(xk−xn)(x−x0)...(x−xk−1)(x−xk+1)...(x−xn)
由此可得插值多项式:
L n ( x ) = ∑ k = 0 n y k l k ( x ) L_n(x)=\sum^n_{k=0}y_kl_k(x) Ln(x)=k=0∑nyklk(x)
称为拉格朗日插值多项式。为了方便表示,引入记号:
ω n + 1 = ( x − x 0 ) ( x − x 1 ) . . . ( x − x n ) 且 有 ω n + 1 ′ ( x k ) = ( x k − x 0 ) . . . ( x k − x k − 1 ) ( x k − x k + 1 ) . . . ( x k − x n ) \omega_{n+1}=(x-x_0)(x-x_1)...(x-x_n)\\ 且有\omega'_{n+1}(x_k)=(x_k-x_0)...(x_k-x_{k-1})(x_k-x_{k+1})...(x_k-x_n) ωn+1=(x−x0)(x−x1)...(x−xn)且有ωn+1′(xk)=(xk−x0)...(xk−xk−1)(xk−xk+1)...(xk−xn)
则拉格朗日插值多项式可以写为:
L n ( x ) = ∑ k = 0 n ω n + 1 ( x ) ( x − x k ) ω n + 1 ′ ( x k ) L_n(x)=\sum^n_{k=0}\frac{\omega_{n+1}(x)}{(x-x_k)\omega'_{n+1}(x_k)} Ln(x)=k=0∑n(x−xk)ωn+1′(xk)ωn+1(x)
关于插值多项式存在惟一性有一个定理:
定理1 在次数不超过n的多项式集合 H n H_n Hn中,满足 L n ( x j ) = y j , ( j = 0 , 1 , . . . , n ) L_n(x_j)=y_j,(j=0,1,...,n) Ln(xj)=yj,(j=0,1,...,n)的插值多项式 L n ( x ) ∈ H n L_n(x)\in H_n Ln(x)∈Hn存在且惟一。
惟一性证明:假定另有 P ( x ) ∈ H n 使 得 P ( x j ) = f ( x j ) , i = 0 , 1 , . . . , n P(x) \in H_n使得P(x_j)=f(x_j),i=0,1,...,n P(x)∈Hn使得P(xj)=f(xj),i=0,1,...,n成立,于是有 L n ( x i ) − P ( x i ) = 0 对 i = 0 , 1 , 2... , n L_n(x_i)-P(x_i)=0对i=0,1,2...,n Ln(xi)−P(xi)=0对i=0,1,2...,n成立,表明多项式 L n ( x i ) − P ( x i ) ∈ H n L_n(x_i)-P(x_i) \in H_n Ln(xi)−P(xi)∈Hn有n+1个零点,这与n次多项式只有n个零点的基本定理矛盾。
eg,已知f(144)=12,f(169)=13,f(225)=15,作f(x)二次Lagrange插值多项式并求f(175)1的近似值。
解: x 0 = 144 , x 1 = 169 , x 2 = 225 , y 0 = 12 , y 1 = 13 , y 2 = 15 x_0=144,x_1=169,x_2=225,y_0=12,y_1=13,y_2=15 x0=144,x1=169,x2=225,y0=12,y1=13,y2=15,则f(x)的二次Lagrange插值基函数为:
l 0 ( x ) = ( x − x 1 ) ( x − x 2 ) ( x 0 − x 1 ) ( x 0 − x 2 ) = ( x − 169 ) ( x − 225 ) ( 144 − 169 ) ( 144 − 225 ) l 1 ( x ) = ( x − x 0 ) ( x − x 2 ) ( x 1 − x 0 ) ( x 1 − x 2 ) = ( x − 144 ) ( x − 225 ) ( 169 − 144 ) ) ( 169 − 225 ) l 2 ( x ) = ( x − x 0 ) ( x − x 1 ) ( x 2 − x 0 ) ( x 2 − x 1 ) = ( x − 144 ) ( x − 169 ) ( 225 − 144 ) ( 225 − 169 ) l_0(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}=\frac{(x-169)(x-225)}{(144-169)(144-225)}\\ l_1(x)=\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}=\frac{(x-144)(x-225)}{(169-144))(169-225)}\\ l_2(x)=\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}=\frac{(x-144)(x-169)}{(225-144)(225-169)} l0(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)=(144−169)(144−225)(x−169)(x−225)l1(x)=(x1−x0)(x1−x2)(x−x0)(x−x2)=(169−144))(169−225)(x−144)(x−225)l2(x)=(x2−x0)(x2−x1)(x−x0)(x−x1)=(225−144)(225−169)(x−144)(x−169)
因此f(x)的二次Lagrange插值多项式为:
L 2 ( x ) = y 0 l 0 ( x ) + y 1 l 1 ( x ) + y 2 l 2 ( x ) L_2(x)=y_0l_0(x)+y_1l_1(x)+y_2l_2(x) L2(x)=y0l0(x)+y1l1(x)+y2l2(x)
知 f ( 175 ) ≈ 12 l 0 175 + 13 l 1 ( 175 ) + 15 l 2 ( 175 ) = 13.23015873 f(175) \approx 12l_0{175}+13l_1(175)+15l_2(175)=13.23015873 f(175)≈12l0175+13l1(175)+15l2(175)=13.23015873
3. 插值余项和误差估计
在[a,b]上用 L n ( x ) L_n(x) Ln(x)近似f(x),则其截断误差 R n ( x ) = f ( x ) − L n ( x ) R_n(x)=f(x)-L_n(x) Rn(x)=f(x)−Ln(x),也称为插值多项式的余项,若f(x)的n阶导数连续,n+1阶导数存在,则:
R n ( x ) = f ( x ) − L n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ω n + 1 ( x ) , 其 中 ξ ∈ ( a , b ) 且 依 赖 于 x R_n(x)=f(x)-L_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\omega_{n+1}(x),其中\xi \in (a,b)且依赖于x Rn(x)=f(x)−Ln(x)=(n+1)!f(n+1)(ξ)ωn+1(x),其中ξ∈(a,b)且依赖于x
通常情况下 ξ \xi ξ在(a,b)上具体位置未知,若可以求出 m a x a < x < b ∣ f ( n + 1 ) ( x ) ∣ = M n + 1 max_{a<x<b}|f^{(n+1)}(x)|=M_{n+1} maxa<x<b∣f(n+1)(x)∣=Mn+1,则 R n ( x ) ≤ M n + 1 ( n + 1 ) ! ∣ ω n + 1 ( x ) ∣ R_n(x) \leq \frac{M_{n+1}}{(n+1)!}|\omega_{n+1}(x)| Rn(x)≤(n+1)!Mn+1∣ωn+1(x)∣。
Lagrange插值多项式的缺点:
-
插值基函数计算复杂
-
当增加一个新点时需重新计算
-
插值多项式从n次增加到n+1次需重新计算
-
插值曲线在节点处有尖点,不光滑,节点处不可导
-
高次插值的精度不一定高
{持续更新}
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]