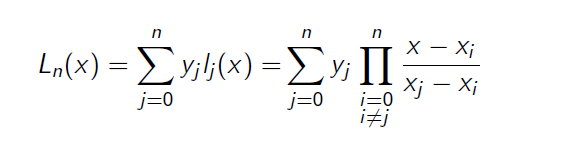拉格朗日插值法求多项式系数（附代码）

article/2025/9/21 20:57:46

写在前面：

学了拉格朗日插值法之后发现大家都说可以在O(n^2)时间内得到多项式系数，但是没有找到代码，网上找了很多资料又因为我太弱了没能看懂，最后在emofunx学长的帮助下终于搞明白了。
由于太弱没能看懂的文章

引入

我们都知道n个点可以确定一个n-1次的多项式F(x)，然后用拉格朗日插值法可以求出这个多项式。
拉格朗日插值法
公式为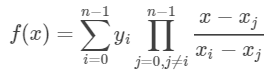：在这里插入图片描述

由这个公式，对于一个数k，我们很容易在O(n^2)时间求得F(k)的数值，如果xi是连续的，我们甚至可以利用预处理在O(n)时间内得到F(k)的数值。
但是如果xi不连续，又有多组查询，就需要得到这个多项式的系数以保证求一个函数值的时间为O(n)。

拉格朗日插值法求系数

首先观察式子，发现对于每个i, 上面部分是(x-x1) * (x-x2)… * (x-xn)/(x-xi), 下面那部分和yi都是常数。
所以可以O(n^2)处理出(x-x1) * (x-x2)… * (x-xn) 这个n次多项式，然后通过模拟长除法，O(n）时间内可以得到(x-x1) * (x-x2)… * (x-xn)/(x-xi)，然后常系数直接O(n) 暴力算出来，就得到了xi对应的多项式，最后把所有多项式加起来就得到了最终的系数。

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 2e3 + 50;
ll mod = 998244353;
ll qm(ll a, ll b){ll res = 1;while(b) {if(b&1)res = res*a%mod;a = a*a%mod, b>>=1;}return res;
}
ll a[maxn], b[maxn], c[maxn], temp[maxn];
ll x[maxn], y[maxn];
int n;
void mul(ll *f, int len, ll t){//len为多项式的次数+1，函数让多项式f变成f*(x+t)for(int i = len; i > 0; --i) temp[i] = f[i], f[i] = f[i-1];temp[0] = f[0], f[0] = 0;for(int i = 0; i <= len; ++i) f[i] = (f[i] + t*temp[i])%mod;
}
void dev(ll *f, ll *r, ll t){//f是被除多项式的系数，r保存f除以x+t的结果for(int i = 0; i <= n; ++i) temp[i] = f[i];for(int i = n; i > 0; --i){r[i-1] = temp[i];temp[i-1] = (temp[i-1] - t*temp[i])%mod;}return;
}
void lglr(){memset(a,0,sizeof a);b[1] = 1, b[0] = -x[1];for(int i = 2; i <= n; ++i){mul(b, i, -x[i]);}//预处理(x-x1)*(x-x2)...*(x-xn)for(int i = 1; i <= n; ++i){ll fz = 1;for(int j = 1; j <= n; ++j){if(j == i) continue;fz = fz*(x[i] - x[j])%mod;}fz = qm(fz, mod-2);fz = fz*y[i]%mod;//得到多项式系数dev(b, c, -x[i]);//得到多项式，保存在b数组for(int j = 0; j < n; ++j) a[j] = (a[j] + fz*c[j])%mod;}
}
int main()
{ll k;cin>>n>>k;for(int i = 1; i <= n; ++i) scanf("%lld%lld",&x[i],&y[i]);lglr();ll ans = 0;ll res = 1;for(int i = 0; i < n; ++i){ans = (ans + res*a[i])%mod;res = res*k%mod;}ans = (ans + mod)%mod;cout<<ans<<endl;
}