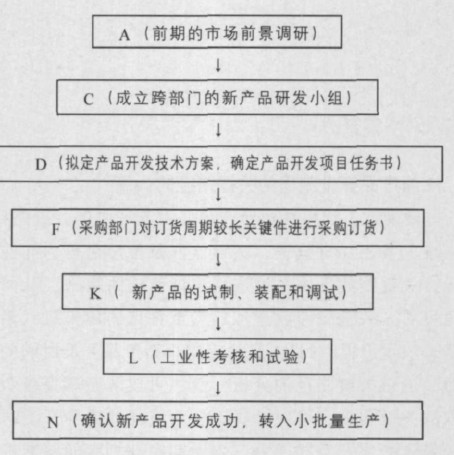
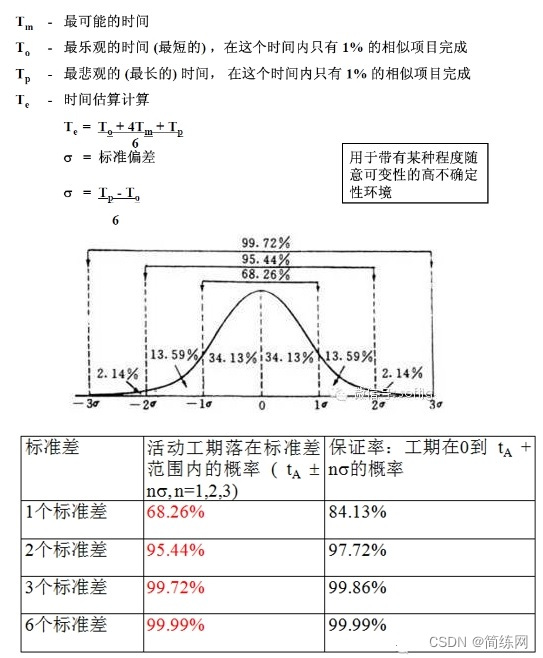
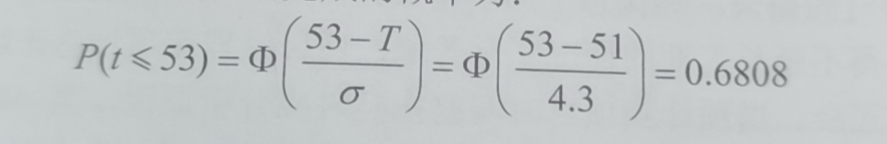题目：

 

基本原理：

 

 

 拉格朗日（Lagrange）插值多项式python实现：

# encoding: utf-8
from symtable  import Symbol
X=[0.4,0.5,0.6,0.7,0.8]
Y=[-0.9163,-0.6931,-0.5108,-0.3567,-0.2231]
print(X,Y)
L=float(0.0)
x=0.54
len=Len(X)
for i in range(0,len):fz=float(1.0)fm=float(1.0)for j in range(0,len):if(i==j):continuefz=fz*(x-X[j])       #算w（x）fm=fm*(X[i]-X[j])l=fz/fm*Y[i]L=L+l
print(L)令
X=[0.4,0.5,0.6,0.7,0.8]
Y=[-0.9163,-0.6931,-0.5108,-0.3567,-0.2231]
#取x下标0 =0.54
#这样便于调试，不用再输入一大堆数据。

结果：

拉格朗日插值法的解果：

E:\shuzhifenxishiyan\Lagrange\venv\Scripts\python.exe E:/shuzhifenxishiyan/Lagrange/main.py

[0.4, 0.5, 0.6, 0.7, 0.8] [-0.9163, -0.6931, -0.5108, -0.3567, -0.2231]

-0.6159832

Process finished with exit code 0