简介

Citus是Postgres的开源扩展，将Postgres转换成一个分布式数据库，在集群的多个节点上分发数据和查询，具有像分片、分布式SQL引擎、复制表和分布式表等特性。
因为Citus是Postgres的扩展(而不是一个独立的代码分支)，所以当你使用Citus时，你也在使用Postgres，可以利用最新的Postgres特性、工具和生态系统。

架构节点

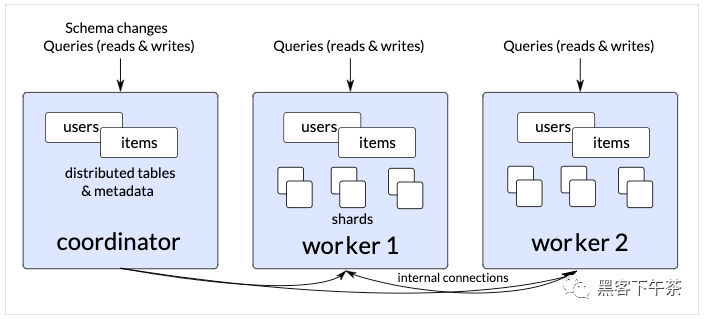
每个集群都有一个称为协调节点（Coordinator Node，CN）的特殊节点，其他节点称为工作节点（Worker Node，WN/DN）。
CN只存储和数据分布相关的元数据，实际的表数据被分成M个分片，打散到N个DN上。
应用程序将它们的查询发送到协调器节点，该节点将查询转发给相关的数据节点并收集结果。

在这里插入图片描述

注：以上以分布式表为例

集群拓扑

首先介绍原生Citus支持的几种集群拓扑

statement-based replication

在这里插入图片描述

为了提高可用性，协调节点通过PG原生流复制实现多副本，数据节点通过基于语句复制实现表级别的副本，副本数由参数shard_replication_factor = 2控制。
基于语句复制存在的问题就是，如果子表非常多，SQL数量成比例增长，压力增加，同时，当子表出现问题时，会标记为非活跃状态，涉及与协调节点通信变更元数据，如果出问题的子表很多，性能自然不会好，相应还会带来副本修复的问题。

在这里插入图片描述

用Raft来做数据复制，每个数据变更都会落地为一条Raft日志，通过Raft的日志复制功能，将数据安全可靠地同步到复制组的每一个节点中。不过在实际写入中，根据Raft的协议，只需要同步复制到多数节点，即可安全地认为数据写入成功。
相比PG本身的主从副本，开发成本比较大，目前Citus已经建议从基于语句的复制切换到流式复制，参数replication_model = ‘streaming’

streaming replication

在这里插入图片描述

协调节点及数据节点都通过流复制实现多副本，保证可用性。
数据节点副本同步使用PG流复制，提高分片上的写入速度。
协调节点属于Master-Standby架构，仅CN节点支持数据写入，势必会有单点可入瓶颈。
另外，默认CN-Stanby的查询发往DN-Primary节点，协调节点虽然做了读写分离，但底层请求都发给了DN-Primary，DN-Standby仅仅充当了备份副本。
对此，Citus还提供了两个参数以支持写入能力扩展及数据节点读写分离。

在这里插入图片描述

use_secondary_node

开启use_secondary_node = always，读请求可以发往数据节点备节点。
writable_standby_coordinator
开启writable_standby_coordinator = on
Enables?simple?DML?via?a?streaming?replica?of?the?coordinator
这个参数的作用就是使CN-Standby也支持DML，比如Insert、Copy等操作。
除了通过writable_standby_coordinator参数支持多节点DML，Citus还提供了MX架构。

Citus MX

在这里插入图片描述

通过MX架构，数据节点同时存储用户数据及元数据，数据读写能力得到了水平扩展。
对于MX架构，数据节点支持存储元数据以支持读写请求，同时也增加了数据节点的压力，对此可以考虑计算存储分离架构。
Citus支持通过函数master_set_node_property设置节点的shouldhaveshards属性，控制DN节点不放分片，专门用于分担CN负载。

在这里插入图片描述