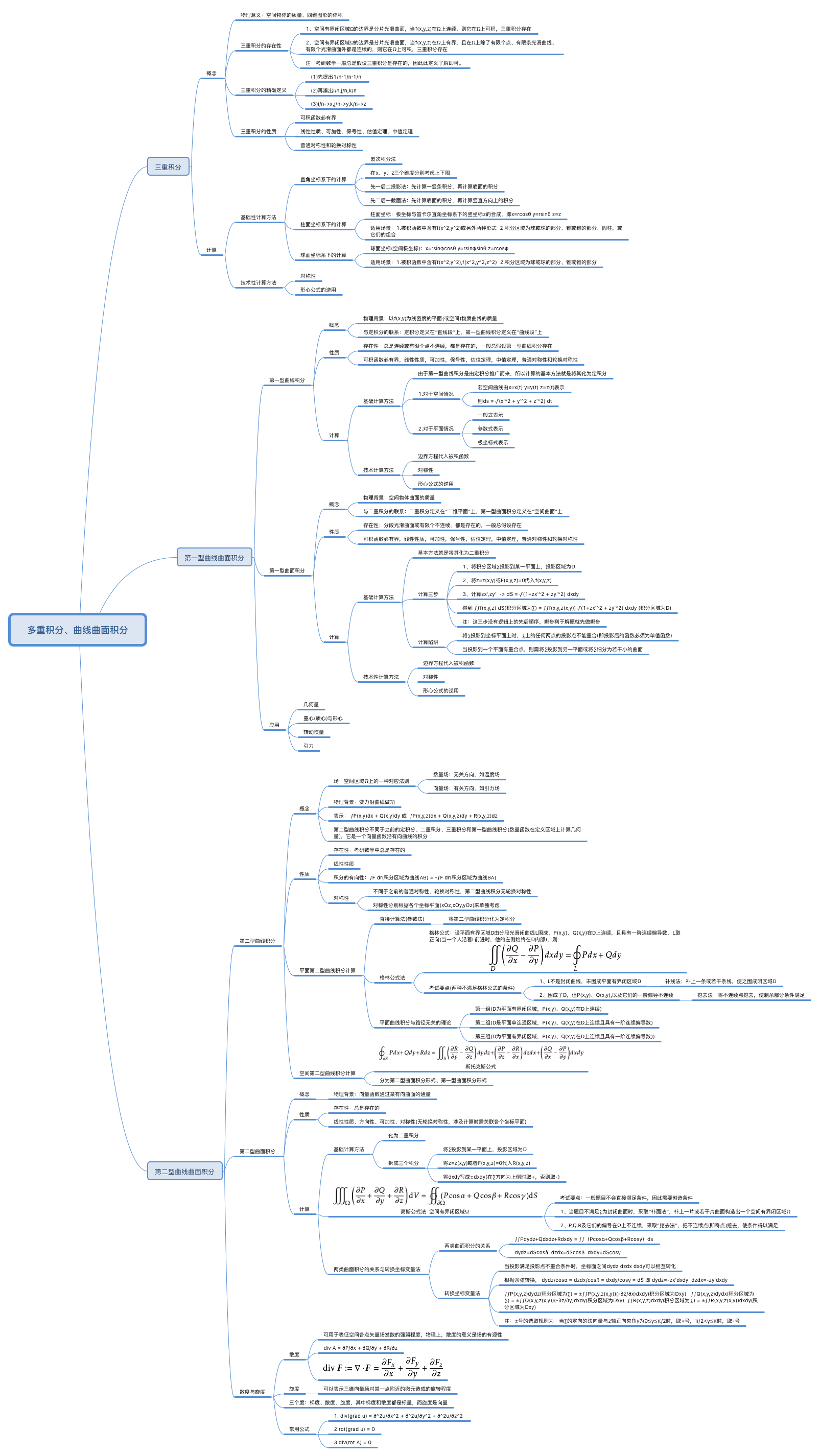
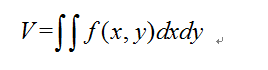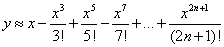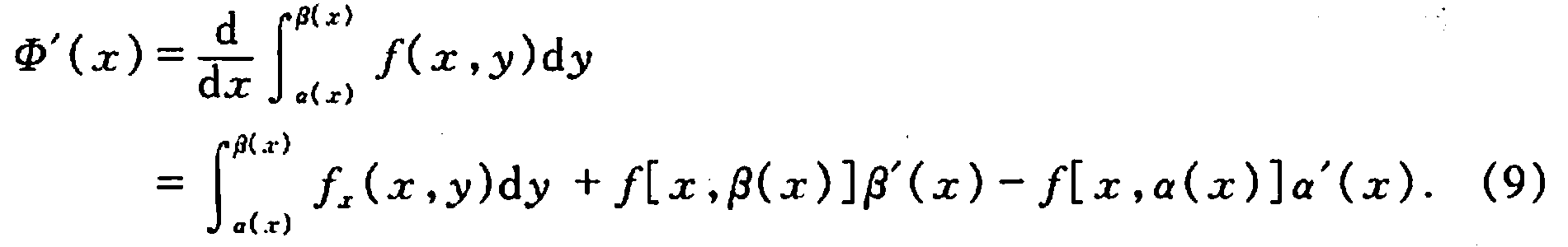作者简介：
迪颉科技是专注于企业数字化转型数据价值及数据治理，并在大数据、数据中台（零售、制造行业）、dataops/数仓以及数据驱动的应用等，提供专业解决方案的团队。在以往外企的从业经验中，将原来的Teradata等数仓大数据的模型/脚本/数据迁移到hadoop/HTAP开放平台，提供工具链和专业的服务及相关的解决方案。
测试时间及人员：
测试时间：2022/9/12 ~ 2022/09/23 测试人员：迪颉科技 项目组
测试背景：
为PG单机版迁移到Citus集群，集群架构与单机 PostgreSQL 的性能特性对比，从读写的效能，以及 SQL 兼容性、业务使用等多个方面进行验证。
测试环境：
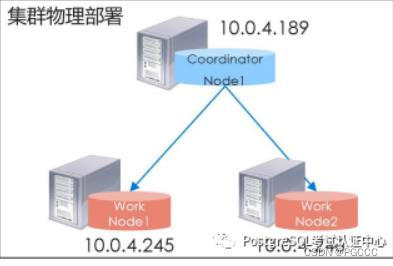
同一台机器，不同数据库，分别是集群_db 和 data_platform 单机（单机）数据库，服务器信息如下：
IP：10.0.4.189 Port：5432
OS：CentOS Linux release 7.8.2003 (Core) CPU：64 vcore Memory：512G，Disk 24T
数据库：PG14.5 à Citus 11.0.6
集群采用一个CN 服务、两个Work
结论：
1、 采用集群（目前 2 节点 worker）后，性能大幅度提升（从 2x~ 42x 不等）
2、 按照生产的 SQL 测试了各类用例，SQL 完全兼容，运行良好
3、 验证了架构的扩展性和各种功能，无异常
4、联络人： Thomas 微信号：a29163631
测试用例：
测试数据信息概况：
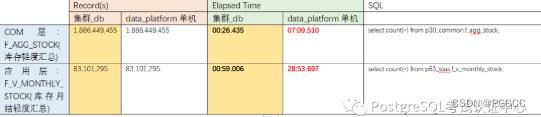
集群按照日期字段（Date_Id）进行数据分布，两者都是分区表，按照日期字段（Date_Id）按月分区。
结论：大表扫描（18 亿），单机 7~28 分钟，集群 26~59 秒
记录数据统计：
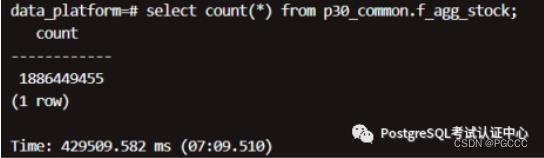
1、单机data_platform 单机，运行结果：
nF_AGG_STOCK
nF_V_MONTHLY_STOCK
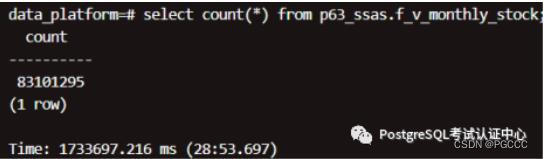
2、集群_db，运行结果：
nF_AGG_STOCK
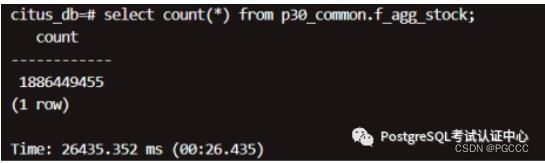
nF_V_MONTHLY_STOCK
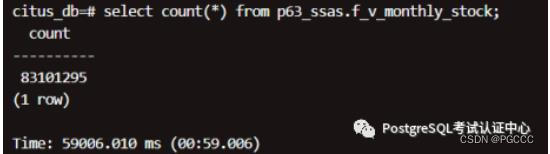
数据关联查询：
结论：2 个大表关联（18 亿 和 8 千 3 百万），单机：4 小时到 7 小时，集群：8 分钟到 11 分钟
单机data_platform 单机，运行结果：
nF_AGG_STOCK
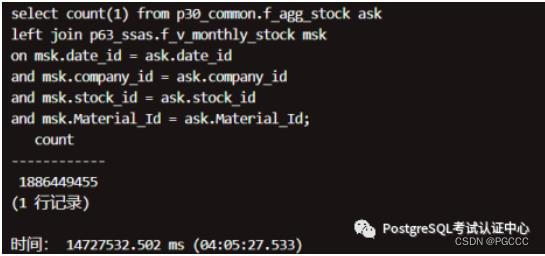
nF_V_MONTHLY_STOCK
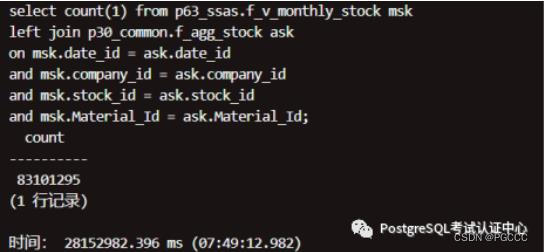
集群_db，运行结果：
nF_AGG_STOCK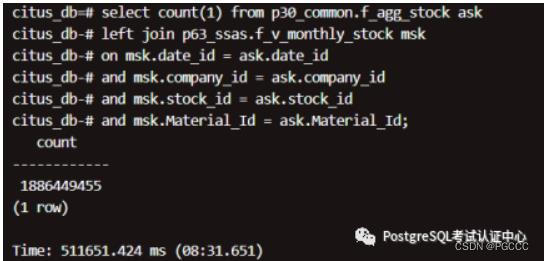
nF_V_MONTHLY_STOCK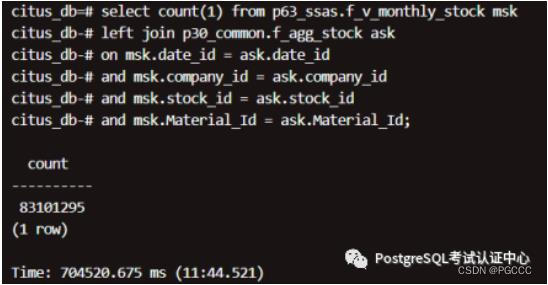
数据关联查询：按照日期聚合
结论：2 个大表（按日期）关联（18 亿 和 8 千 3 百万），单机：6 小时到 7 小时，集群：12 分钟到 17 分钟
单机data_platform 单机，运行结果：
nF_AGG_STOCK
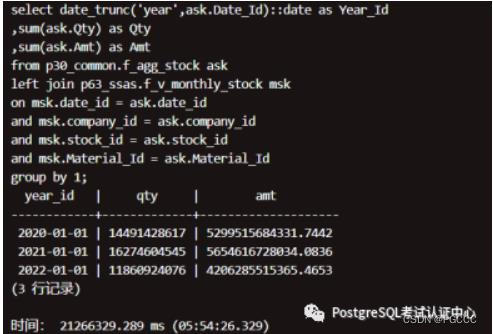
nF_V_MONTHLY_STOCK
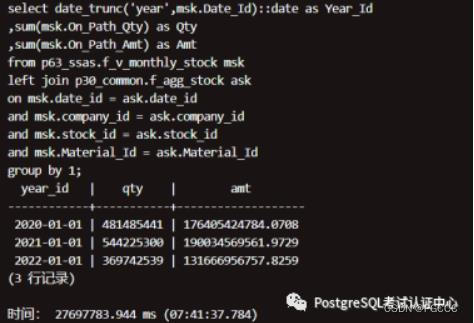集群_db，运行结果：
nF_AGG_STOCK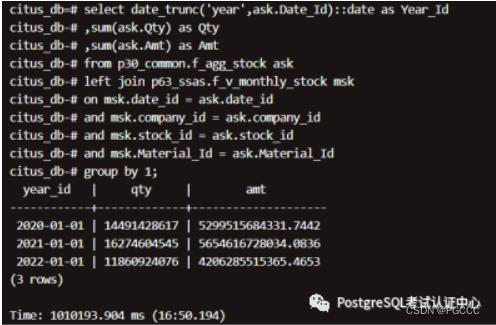
nF_V_MONTHLY_STOCK
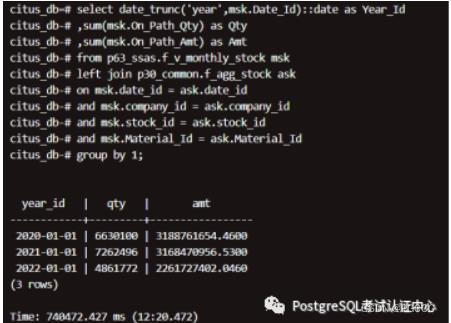
数据关联查询：按照经营渠道聚合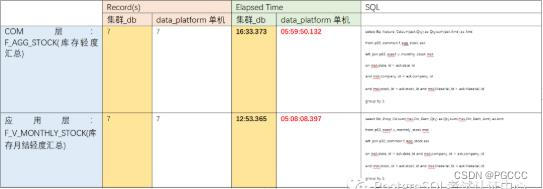
结论：2 个大表（按经营渠道）关联（18 亿 和 8 千 3 百万），单机：5 小时到 5 小时，集群：12 分钟到 17 分钟
单机data_platform 单机，运行结果：
nF_AGG_STOCK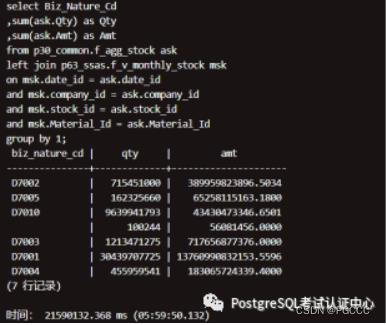
nF_V_MONTHLY_STOCK
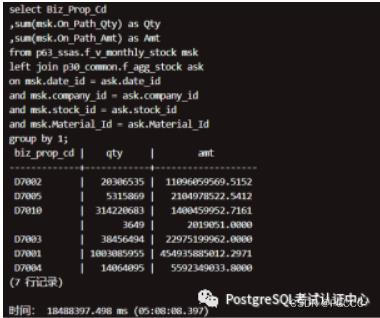
集群_db，运行结果：
nF_AGG_STOCK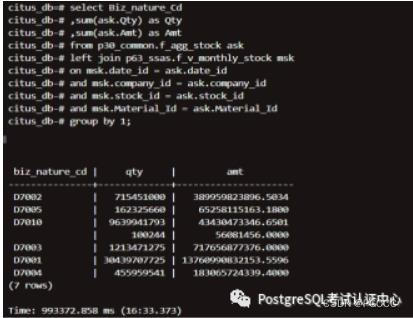
nF_V_MONTHLY_STOCK
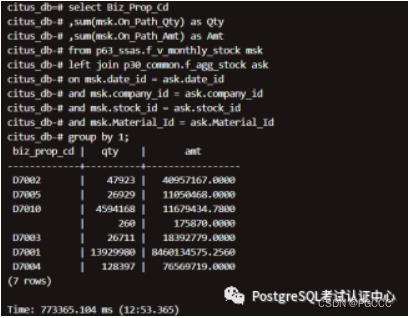数据更新处理：
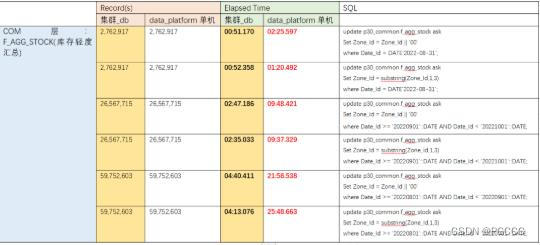
结论：单个大表（18亿），更新2百7万，单机：平均1分23秒，集群52秒；更新2前7万，平均9分43秒，集群：2分41秒；更新5千9万，平均23分53秒，集群：4分27秒；
单机data_platform 单机，运行结果：
nF_AGG_STOCK:2022-08-31(更新)
nF_AGG_STOCK:2022-08-31(修复)
nF_AGG_STOCK:9 月份(更新)
nF_AGG_STOCK: 9 月份(修复)
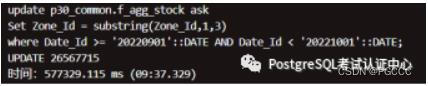
nF_AGG_STOCK: 8 月份(更新)
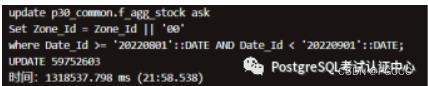
nF_AGG_STOCK: 8 月份(修复)
集群_db，运行结果：
nF_AGG_STOCK:2022-08-31(更新)
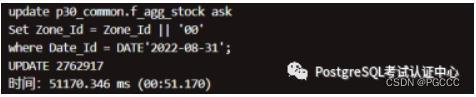
nF_AGG_STOCK:2022-08-31(修复)
nF_AGG_STOCK:9 月份(更新)
nF_AGG_STOCK: 9 月份(修复)
nF_AGG_STOCK: 8 月份(更新
数据写入处理：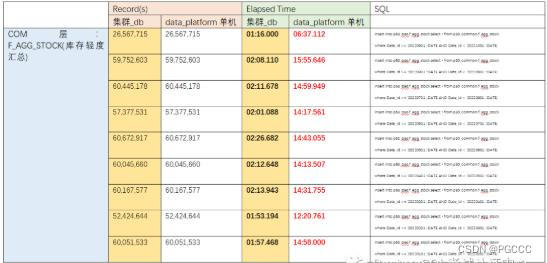
结论：源表（18 亿），加载 2 百 7 万，单机：平均 6 分 37 秒，集群：1 分 16 秒； 加载 6 千万左右，平均 14 分 30 秒，集群：2 分 8 秒；
单机data_platform 单机，运行结果：
nF_AGG_STOCK_VERIFY:2022 年 9 月份
nF_AGG_STOCK_VERIFY:2022 年 8 月份
nF_AGG_STOCK_VERIFY:2022 年 7 月份
nF_AGG_STOCK_VERIFY:2022 年 6 月份
nF_AGG_STOCK_VERIFY:2022 年 5 月份
/635aa53c9a5d46da922a6abe0a50dde7.jpeg
nF_AGG_STOCK_VERIFY:2022 年 4 月份
集群_db 运行结果：
nF_AGG_STOCK_VERIFY:2022 年 9 月
nF_AGG_STOCK_VERIFY:2022 年 8 月份
nF_AGG_STOCK_VERIFY:2022 年 7 月份
nF_AGG_STOCK_VERIFY:2022 年 6 月份
nF_AGG_STOCK_VERIFY:2022 年 5 月份
/ba94d93572324ade80033c3591f24d7f.jpeg
nF_AGG_STOCK_VERIFY:2022 年 4 月份
单机data_platform 单机，运行结果：
nF_AGG_STOCK_VERIFY:2022 年 3 月份
nF_AGG_STOCK_VERIFY:2022 年 2 月份
nF_AGG_STOCK_VERIFY:2022 年 1 月份
集群_db 运行结果：
nF_AGG_STOCK_VERIFY:2022 年 3 月份
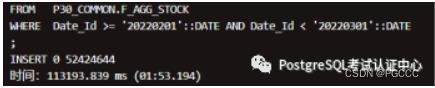
nF_AGG_STOCK_VERIFY:2022 年 2 月份
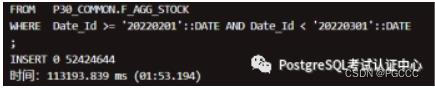
nF_AGG_STOCK_VERIFY:2022 年 1 月份
