点击上方"数据和云"
关注我们,享更多干货!
1. Citus的复制功能
Citus支持两种数据复制方案:
Citus的Shard Replication:通过将DML语句复制到多个Worker节点执行,实现对shard分片数据的复制,仅适用于append-only的负载;当某个Worker节点故障时,Coordinator节点会自动将查询请求转发到其他副本节点以实现高可用;
PostgreSQL的Streaming Replication:通过将Primary节点的WAL记录持续的复制到Standby节点,实现对Primary节点的完整复制,适用于负载较重的OLTP场景;
为什么会同时存在两种方案呢?可以看看Citus复制功能的演进过程。
1.1 第一阶段:客户端复制DML语句到多个Worker节点
在早期的版本中,Citus的主要应用场景是实时数据分析场景,用户批量的导入数据,并通过Citus进行实时数据查询分析,数据不需要修改,是完全Append-only的场景。
Append-Only的场景,各分片数据只需要在完成导入后是一致的就行,为了最大化导入性能,可以从客户端直接并行导入。
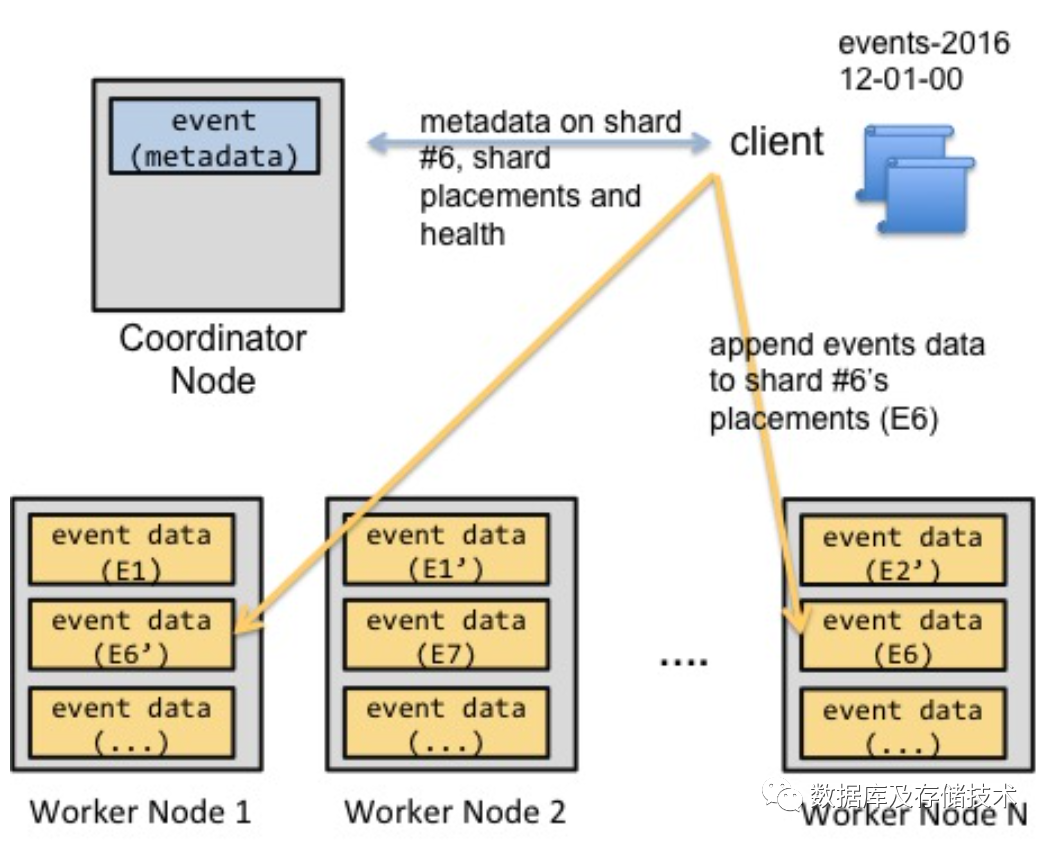
这个阶段,Citus导入数据的流程如下:
客户端通知Coordinator需要导入数据到某个表;
Coordinator节点分配对应的placement,并反馈连接信息给客户端;
客户端直接连接对应Shard及其副本,同时往多个副本写入数据;
客户端通知Coordinator更新元数据。
1.2 第二阶段:Coordinator复制DML语句到多个Worker节点
随着使用Citus的人越来越多,对于提供数据更新能力的需求也越来越多。为了提供数据更新能力,Citus需要解决两个主要的问题:
并发更新同一行记录,如何处理?
某个Shard副本不可用,如何处理?
为了解决引入数据更新能力的问题,Citus将更新操作集中到了Coordinator节点,由集中的Coordinator节点处理并发冲突和故障处理。
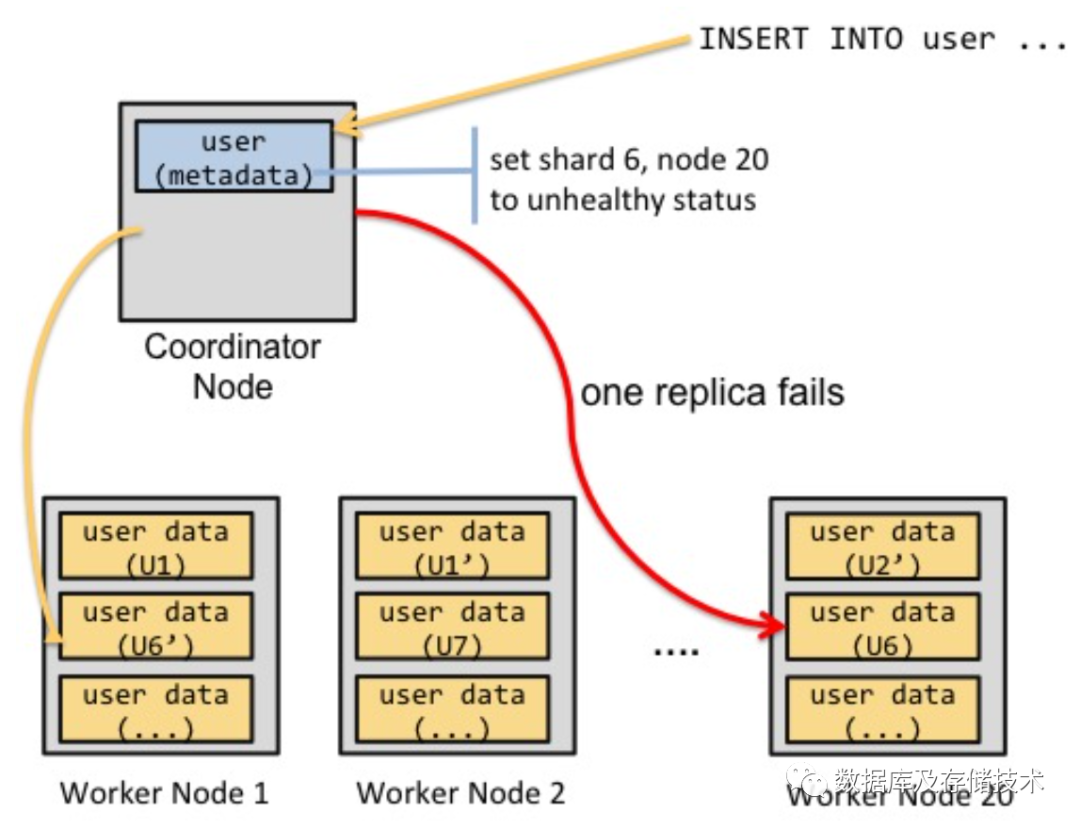
此时,数据的多副本复制,改成了由Coordinator节点复制DML语句到多个Worker节点执行。
1.3 第三阶段:推荐使用Streaming Replication
随着使用Citus的场景增加,例如多租户的场景,Citus引入了Co-located亲和性共存能力,可以把相同租户的数据亲和性存储在同一个Worker节点,方便支持Join查询,Rollup、外键约束等特性。
此时,前面基于复制Statment的复制方案就会碰到问题,当某个Shard因为短时故障被标记为invalid时,应该如何处理处于同一个Co-located亲和组的其他Shard?
不同步修改其他Shard状态,可能会引发违反外键约束的一致性问题;
同步修改其他Shard都为invalid状态,系统的可用性会严重下降。
这是一个两难的问题,为了安全起见,Citus在6.0版本中把复制因子的默认值从2改为了1,就是因为多租户场景下可能会产生违反外键约束的问题。
现在,Citus推荐的是使用PostgreSQL的Streaming Replication,如下图所示,Streaming Replication是primary-based replication,由主节点解决并发控制问题。
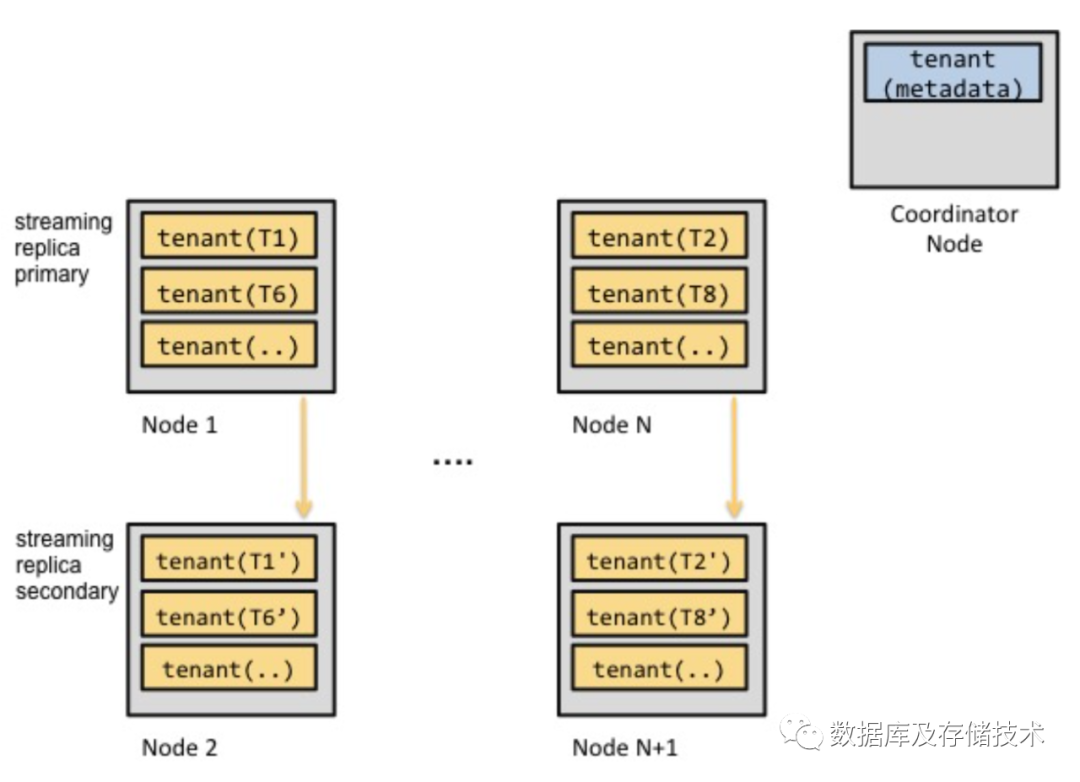
2. 云上Citus高可用备选方案
2.1 备选一:Streaming Replication
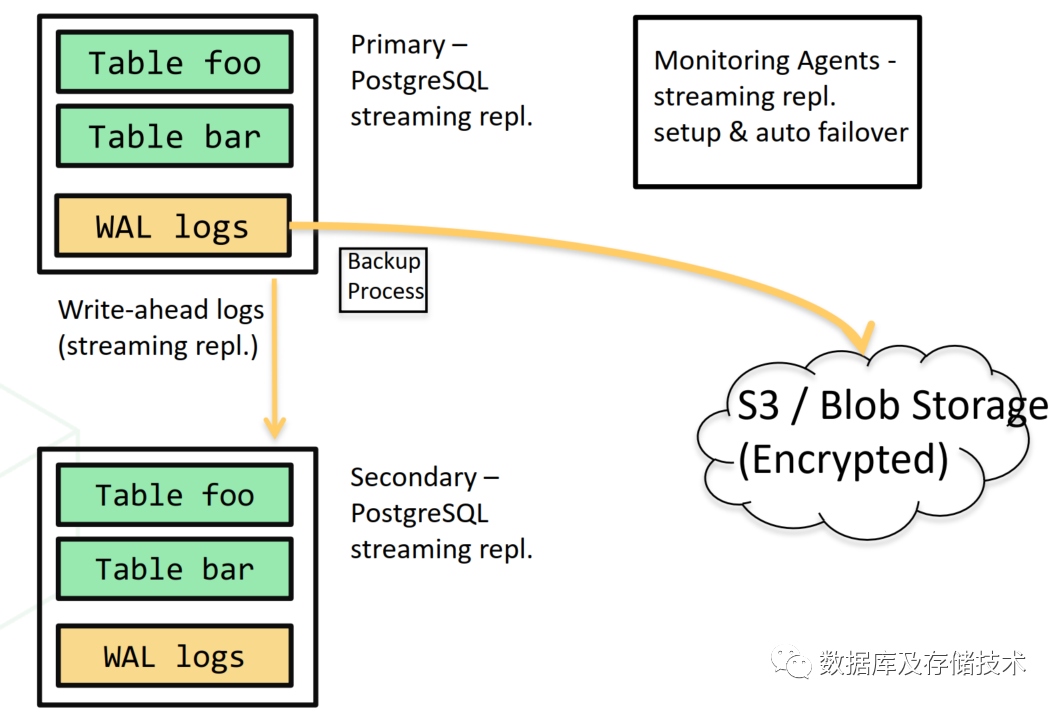
如前面描述,Streaming Replication是PostgreSQL的内置特性,通过将WAL记录持续复制到Standby节点,建立Hot Standby备份节点。
2.2 备选二:镜像卷
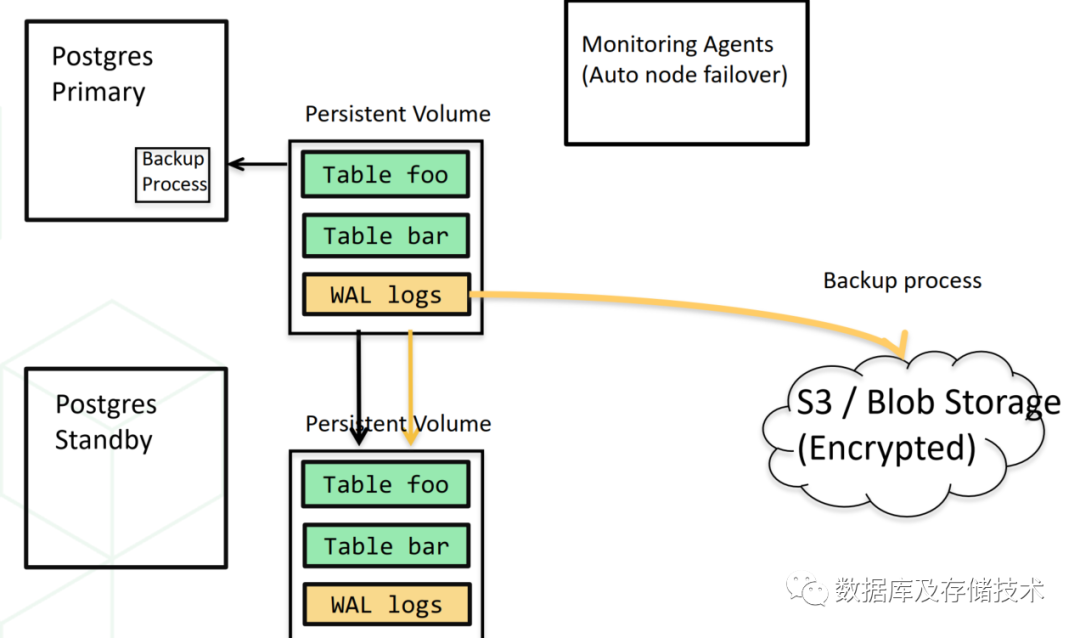
在云上,也可以使用云提供商的镜像卷能力,当Primary节点故障时,在对应备份卷的主机上拉起数据库进程接管业务。
2.3 备选三:从日志恢复
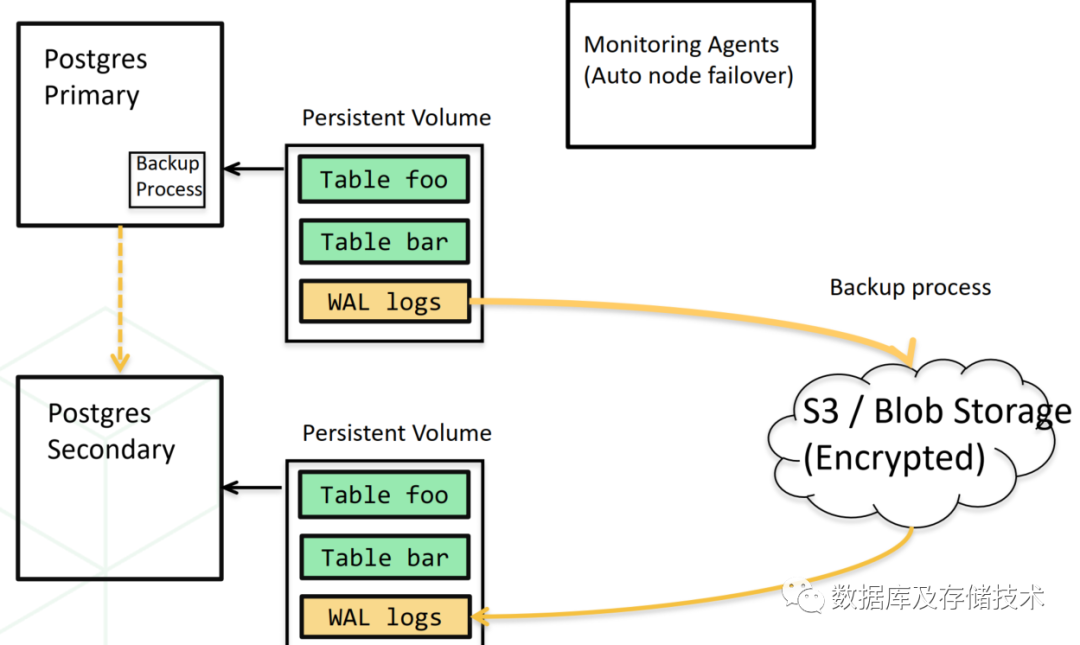
如果对RTO业务恢复时间不太敏感,也可以采用将WAL日志增量备份到对象存储的方式,本方案的成本更低,故障后,拉起对应计算节点,从对象存储恢复日志并重放数据即可。
2.4 备选方案对比
备选方案 | 优点 |
Streaming Replication | 简单方便,需要更高的存储IO能力及容量; |
镜像卷 | 利用云存储的高持久性和稳定性; |
从日志恢复 | 利用云存储的高持久性,可以实现PITR。 |
2.5 Azure Hyperscale (Citus)的高可用方案
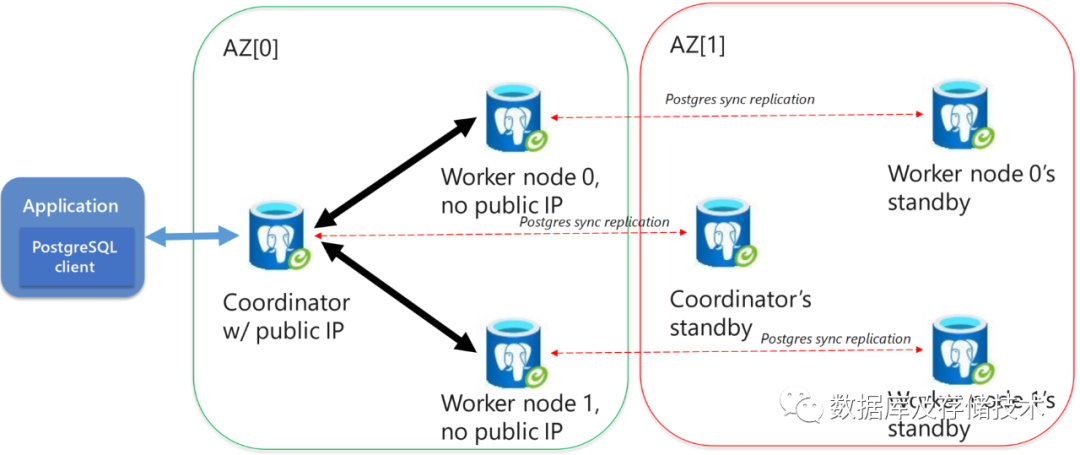
Coordinator节点和Worker节点都使用Streaming Replication方案将数据同步复制到位于另一个AZ的Standby节点,支持AZ级的容灾。主要技术指标有:
故障检测:每30秒检测一次,连续5次检测都异常则判断为故障,总计150秒;
故障倒换:最高90秒完成;
业务影响时间:检测 + 倒换时间,总计240秒;
新建Standby节点时间:不超过1小时。
参考
https://www.citusdata.com/blog/2016/12/15/citus-replication-model-today-and-tomorrow/
https://github.com/citusdata/citus/issues/998
#
Citus简介
Citus是PostgreSQL数据库的分布式中间件,用以解决PostgreSQL横向扩展问题,以支持更大的数据量、更大的写入和查询性能。
Citus由CitusData公司开发,目前已被微软收购,并在Azure上提供Citus Cloud服务。Citus为开源软件,经过约10年的发展,最近刚发布10.0版本,License为AGPL。
不像pg-xc的原生分布式方案,Citus是以Extension的方式扩展PostgreSQL能力,不侵入修改PostgreSQL内核代码,可以很容易和PostgreSQL的新版本配套适用,享受到内核版本演进带来的好处。
关于作者
张程伟,云和恩墨资深数据库架构师,加入云和恩墨前在华为工作16年,一直从事存储及数据库领域的研究工作。
END


MySQL/PG/Oracle DBA
数据库专家(售前)、销售总监/经理

200+热招职位 覆盖全国40+所城市
由ACDU(中国DBA联盟)和墨天轮联合出品的全新视频节目「数据三分钟」已发布多期,快速了解数据行业动态,快关注我们的视频号看看吧!↓↓↓
点击下图查看更多 ↓



云和恩墨大讲堂 | 一个分享交流的地方
长按,识别二维码,加入万人交流社群
请备注:云和恩墨大讲堂
点个“在看”
你的喜欢会被看到❤