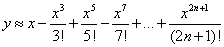一． Citus是什么

Citus是一个PostgreSQL扩展，它允许数据库服务器（即节点）在一个Shared Nothing的架构中彼此协调。这些节点形成了一个集群，使得PostgreSQL能够比一台计算机使用更多的CPU内核来存储更多的数据，同时还允许通过向集群添加更多节点来扩展数据库。

官方文档：Citus Documentation — Citus 10.0 documentation (citusdata.com)

优势：Citus适合做单表查询，且该单表数据量越大，Citus的优势就越明显。

劣势：Citus集群相对于单机PostgreSQL，对SQL有一些支持不完善的地方，对regregate函数支持不好，要求必须可以分解。实际上PostGIS中很多聚集函数都不支持，例如ST_ClusterWithin，st_extent。

主要特性：

• PostgreSQL兼容
• 水平扩展
• 实时并发查
• 快速数据加载
• 实时增删改查
• 持分布式事务
• 支持常用DDL

二． Citus架构节点

Container简称CN节点，CN只存储和数据分布相关的元数据，实际的表数据被分成M个分片，打散到N个Worker上。这样的表被叫做“分片表”，可以为“分片表”的每一个分片创建多个副本，实现高可用和负载均衡。分片表分布打散在多个worker节点，而参考表每一个container节点和worker都保留一模一样的副本。

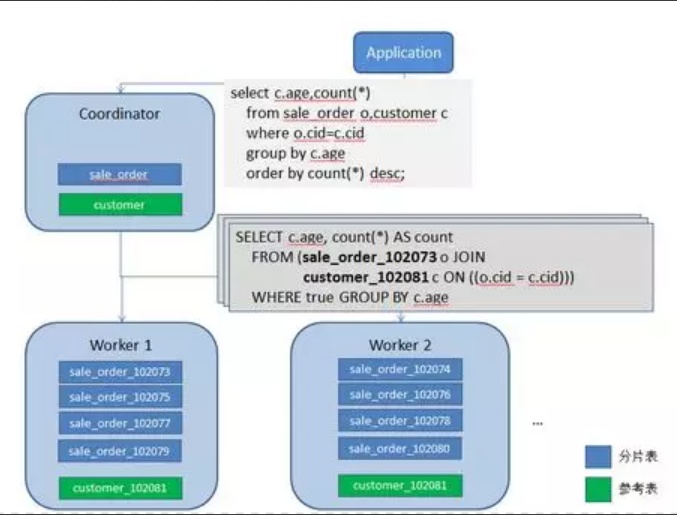
下图是Citus处理客户端访问的一个简单的架构流程图，应用层直接连接CN节点，CN节点对客户端传入的sql语句进行解析，生成分布执行计划，并将各个子任务下发到相应的Worker节点，之后收集Worker的结果，经过处理后返回最终结果给客户端。最基本的流程就是这样，但是生成环境我们还应该考虑到高可用。

三． Citus对odoo的兼容

Citus能够兼容odoo。已在实际环境中测试， odoo13和odoo14均可以搭建在Citus数据环境中，并正常运行，包括安装、卸载odoo应用和应用中各项数据的增、删、改、查。

数据架构：

运行截图：

四． Citus的扩缩容

citus企业版中可以进行动态扩容，社区版中尚不支持动态扩容。不过我们可以通过修改元数据表中的分片信息来实现类似的功能。

我们可以通过citus自带的master_add_node函数来添加节点到集群中，现有的参考表可以自动分布到新的节点中，但是分片表却不可以自动同步到新的work节点中。

对于分片表，我们则需要手动移动这些分片，大致步骤为：

1、 表复制

在移动目标分片的源端和目的端建立复制。

2、 元数据切换

加锁，阻塞相关的分片表的数据变更；

修改pg_dist_shard_placement元数据表，变更分片位置信息。

3、 清理

DROP切换前的旧的分片。

版权声明:本文由神州数码云基地团队整理撰写，若转载请注明出处。
公众号搜索神州数码云基地，后台回复Odoo，加入Odoo技术交流群！