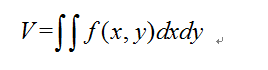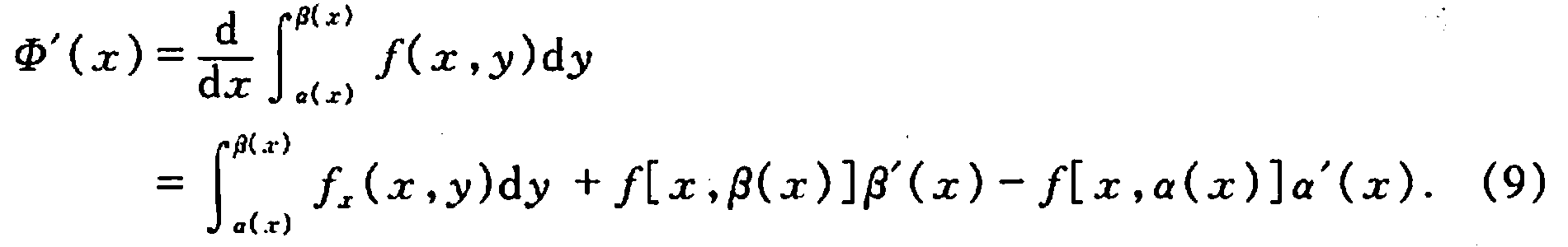目录
- 哈密顿算子(Hamiltionian) ∇ \nabla ∇
- 标量性质
- 矢量性质
- 拉普拉斯算子(Laplace) Δ \Delta Δ
- 标量性质
- 矢量性质
- 格林公式高斯公式和斯托克斯公式
- 多重积分的分部积分公式
哈密顿算子(Hamiltionian) ∇ \nabla ∇
标量性质
u ( x , y ) u(x,y) u(x,y)是一个标量函数,
∇ u = ( u x u y ) \nabla u=\begin{pmatrix} u_x \\ u_y \\ \end{pmatrix} ∇u=(uxuy) 表示梯度
矢量性质
u = ( u 1 u 2 ) u=\begin{pmatrix} u_1 \\ u_2\\ \end{pmatrix} u=(u1u2) 是矢量场(矩阵也可以)
∇ ⋅ u ⃗ = u T ( ∂ ∂ x ∂ ∂ y ) \nabla ·\vec{u}=u^T\begin{pmatrix} \frac {\partial }{\partial x} \\ \frac {\partial }{\partial y}\\ \end{pmatrix} ∇⋅u=uT(∂x∂∂y∂)
∇ ⋅ u ⃗ \nabla ·\vec{u} ∇⋅u 点乘是散度

∇ × u ⃗ = ∣ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z u 1 u 2 u 3 ∣ \nabla \times \vec{u}= \begin{vmatrix} i&j&k\\ \frac {\partial }{\partial x} &\frac {\partial }{\partial y}&\frac {\partial }{\partial z}\\ u_1&u_2&u_3\\ \end{vmatrix} ∇×u=∣∣∣∣∣∣i∂x∂u1j∂y∂u2k∂z∂u3∣∣∣∣∣∣
∇ × u ⃗ \nabla \times\vec{u} ∇×u 点乘是旋度【此时u是向量,如果是矩阵呢?】

拉普拉斯算子(Laplace) Δ \Delta Δ
标量性质
Δ u = ∇ ⋅ ∇ u = ∇ 2 u = u x x + u y y \Delta u=\nabla ·\nabla u=\nabla^2 u=u_{xx}+u_{yy} Δu=∇⋅∇u=∇2u=uxx+uyy
矢量性质
Δ u = ∇ ( ∇ ⋅ A ) − ∇ × ( ∇ × A ) = ( Δ u 1 Δ u 2 ) \Delta u=∇(∇⋅A)−∇×(∇×A)=\begin{pmatrix} \Delta u_1 \\ \Delta u_2\\ \end{pmatrix} Δu=∇(∇⋅A)−∇×(∇×A)=(Δu1Δu2)
此时等同于对u的每个分量拉普拉斯算子
格林公式高斯公式和斯托克斯公式
格林公式

高斯公式

斯托克斯

多重积分的分部积分公式
1. ∫ ∂ Ω ∂ u ∂ n d σ = ∫ Ω Δ u d μ \int_{\partial_{\Omega}}\frac {\partial u}{\partial \bold{n}}d\sigma=\int_{\Omega}\Delta ud\mu ∫∂Ω∂n∂udσ=∫ΩΔudμ
2. ∫ ∂ Ω v ∂ u ∂ n d σ = ∫ Ω ∇ u ⋅ ∇ v d μ + ∫ Ω v Δ u d μ \int_{\partial_{\Omega}}v\frac {\partial u}{\partial \bold{n}}d\sigma=\int_{\Omega}\nabla u ·\nabla v d\mu+\int_{\Omega}v\Delta ud\mu ∫∂Ωv∂n∂udσ=∫Ω∇u⋅∇vdμ+∫ΩvΔudμ
3. ∫ ∂ Ω ( v ∂ u ∂ n − u ∂ v ∂ n ) d σ = ∫ Ω ( v Δ u − u Δ v ) d μ \int_{\partial_{\Omega}}(v\frac {\partial u}{\partial \bold{n}}-u\frac {\partial v}{\partial \bold{n}})d\sigma=\int_{\Omega}(v\Delta u-u\Delta v)d\mu ∫∂Ω(v∂n∂u−u∂n∂v)dσ=∫Ω(vΔu−uΔv)dμ