码分多址
- 对于码分多址(也叫码分复用)种,每一个用户可以在同样的时间选择同样的频带进行通信。
- 由于用户使用经过特殊挑选的不同码型,因此各用户之间不会造成干扰。
- 码分复用最初是用于军事通信的,因为这种系统发送的信号具有很强的抗干扰能力,其频谱类似于白噪声,不易被敌人发现。
我们首先了解码片的概念:
码片:指的是在CDMA中,每一个比特时间在划分成m个短的间隔,称为码片,通常m的取值是64或者128。为了讲解方便我们后续码片的大小假设为8。
码分多址中,为了实现多用户同时通信而互补干扰,要求每个发送信号的站都使用不同的码片 。也就是说使用CDMA的每一个站都被指派了一个唯一的mbit的码片序列。
关于码片序列还有以下规定:
- 一个站如果要发送比特1,则发送他自己的mbit码片序列。
- 一个站如果要发送比特0,则发送自己的mbit码片序列的反码。
例如:

这种通信方式称为序列扩频DSSS。
对于码片的挑选有以下原则:
- 分配给每个站的码片序列必须各不相同。
- 分配给每个站的码片序列必须相互正交(规格化内积为零)。
至此就引出了我们计算码分多址的相关计算核心公式:
规格化内积计算公式:

S和T的规格化内积为0,就是将S和T中的对应分量相乘,再相加,再除以向量中分量的数量。
例如:
假设:
码片序列S为:(-1 +1 -1 +1 +1 +1 -1 +1)。
码片序列T为:(+1 -1 +1 +1 +1 -1 -1 -1)。
向量中分量数量就是括号内数字的个数。
可知其向量中分量数量8.
就是各个分量相乘并且累加,再除以分量数量。
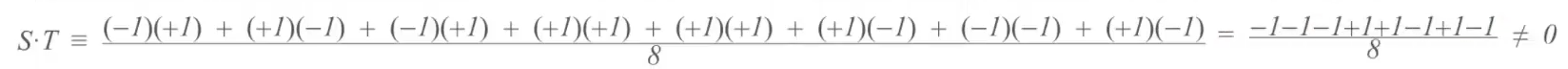
在此例中不等于零,若是选择码片,则此S和T码片序列不可选。
不仅如此,我们可以得出结论(后面要用到):
在码分多址中,任何一个站和其他各占的码片反码的向量的内积也是0。
任何一个码片向量和自己码片反码的向量的内积为-1
任何一个码片向量和自己码片反码的向量的内积为1
(可以自己进行推算证明)
第一种题目:
判断码片选择是否合适:

在这种题中,只要明白选择码片的两个条件:
- 码片序列各不相同
- 码片正交(规格化内积为零)
便可以判断是否是正确分配的码片,很明显在此题中不是。
第二种题目:
判断接收到叠加信号后,判断某基站发送的信号类型。
首先需要明确的是,由于CDMA中码片的特性,码片之间都是相互正交的,也就是可以理解为两个向量之间加夹角为90°,根据向量的计算公式:
a·b=|a||b|cosθ。
可以得出其值为零。
那么这对我们的题目有什么用处呢?
对于叠加的码片序列,可以看成是一个个向量,所有码片序列都是相互正交的,假如我们想知道某个叠加信号中某基站的信号情况,只要用该信号与叠加信号相乘,就可以排除其他所有向量的干扰(某向量和其他向量都相互垂直,乘积为零)。
因此可以得出一个结论:
接收端用相同的码片序列进行规格化内积,就可以将不属于本码片序列的其他信号全部去除。
再结合上面的结论:
可得出:
对于叠加向量中要计算某一基站的码片发送了什么信号,用该码片与叠加信号相乘:
其结果为1,说明该基站发送信号为1
其结果为-1,说明该基站发送信号为0
其结果为0,说明该基站没有发送信号
牢记此结论,开始做题:
例如:

在此CDMA中,假设所有站所发送的码片序列都是同步的,接收站D知道其他各站的码片序列,现在需要接收站D对所接收到的叠加信号进行计算:

习题2:

计算思路:
用收到的码片序列分别与各站的码片序列进行内积运算,再结合上面的结论:
若计算结果为1,则被判断的站发送了比特1;
若计算结果为-1,则被判断的站发送了比特0;
若计算结果为0,则被判断的站未发送数据;
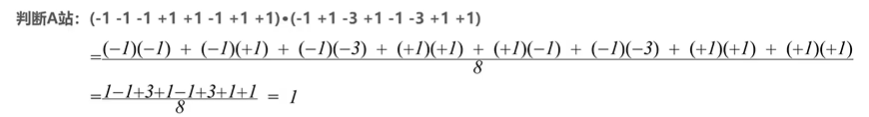
可知A站发送信号为比特1。
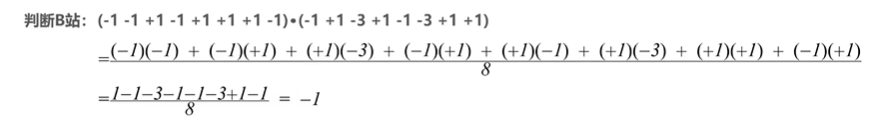
可知,B站发送信号为0。
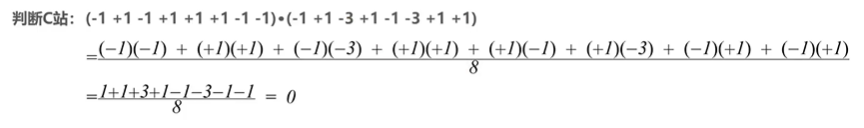
可知,C站没有发送信号。
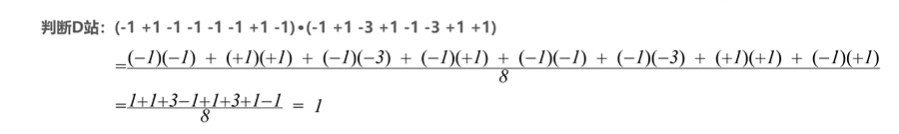
可知,D站发送的信号为1。
考研真题:

题目解析:

因此可知,A发送的数据是101,答案选择B。
如果觉得文章写的还不错,麻烦点个赞支持一下,欢迎评论,互相交流学习。