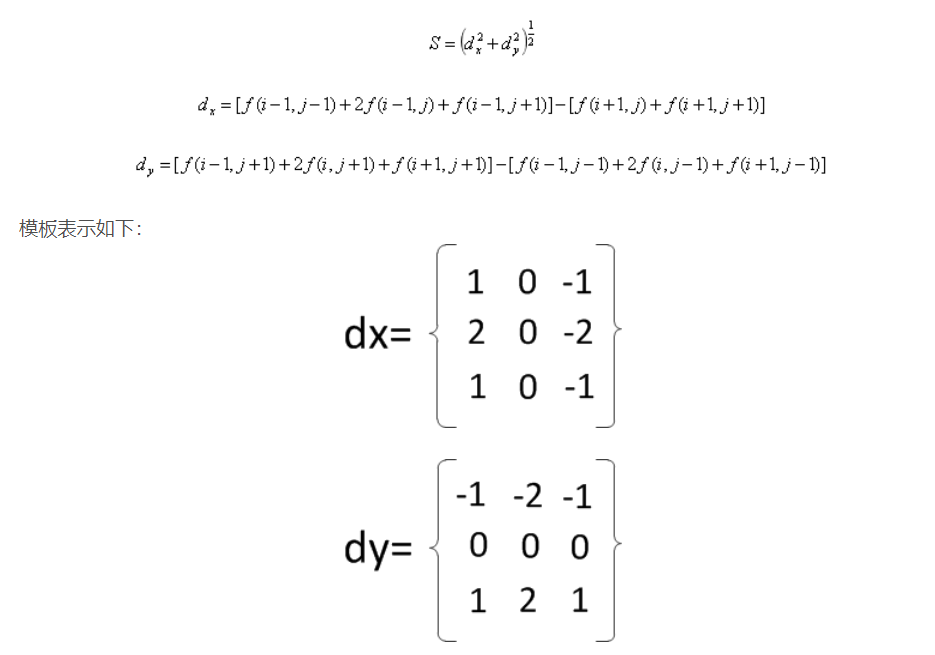
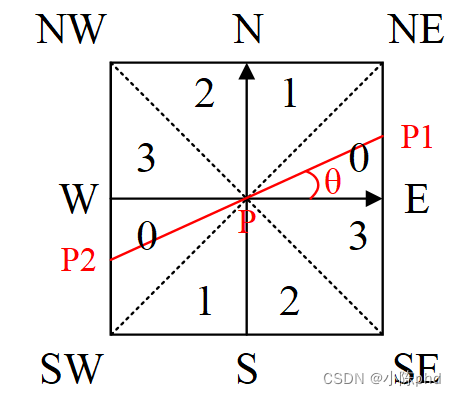
用于边缘检测的算子应该有两个显著的特点：
1.它应该能够计算图中每一个点处的一阶导数或者二阶导数的数字近似的微分算子。
2.它能够被“调整”以便在任何期望的尺寸上其作用。因此，大的算子也可以用于检测模糊边缘，小的算子可以用来检测锐度集中的精细细节。

满足上面两个要求的最好算子是滤波器${\nabla }^{2}G$其中${\nabla }^2$是拉普拉斯算子，而G是标准差为$\sigma$的二维高斯函数。
我们简称其为高斯拉普拉斯（LoG）：

选择${\nabla }^{2}G$的原因如下：
1.算子的高斯部分会模糊图像，从而在尺寸上将结构的灰度（包括噪声）降低到远小于$\sigma$的程度。
2.高斯函数在空间和频率两个域平滑图像，因而在原图像中引入不存在的人为干扰（如振铃）的可能性较小。
3.尽管一阶导数可用于检测灰度突变，但是它们是有方向的算子，而拉普拉斯有各项同性（旋转不变）的特点。

如何构造log算子模板:
目的：获取LOG函数的基本形状，这意味着一个正的中心项由紧临的负区域包围着，中心项的值以距原点的距离为函数而增大，而外层区域的值为零。系数之和必须为零，从而模板的响应在恒定灰度区域为零。

大小：为确定高斯滤波器的大小，仍采用位于二维高斯表面下其均值在正负$3\sigma$之间的99.7%，作为一种经验法则，一个大小为n*n的LOG离散滤波器，其n值应是大于等于$6\sigma$的最小奇数。n小于该值的滤波器模板会“截断”LOG函数，截断的程度与模板的大小成反比；而是用较大的模板对结果的影响不大（因为超过6$\sigma$的地方数值为0）。

我们知道二阶导数对边缘检测会产生零交叉，于是我们接下来要做的就是对上一步得到的的图像寻找零交叉，我们一般以3*3的领域寻找零交叉。