二阶微分边缘算子

二阶微分边缘算子基本思想

• 边缘即是图像的一阶导数局部最大值的地方，那么也意味着该点的二阶导数为零。

• 二阶微分边缘检测算子就是利用图像在边缘处的阶跃性导致图像二阶微分在边缘处出现零值这一特性进行边缘检测的。

对于图像的二阶微分可以用拉普拉斯算子来表示：
${\nabla }^{2}I=\frac{{\partial }^{2}I}{\partial x^2}+\frac{{\partial }^{2}I}{\partial y^2}$
我们在像素点(i,j)的3×3 的邻域内，可以有如下的近似：
$\frac{{\partial }^{2}I}{\partial x^2}=I(i,j+1)-2I(i,j)+I(i,j-1)$
$\frac{{\partial }^{2}I}{\partial y^2}=I(i+1,j)-2I(i,j)+I(i-1,j)$
${\nabla }^{2}I=-4I(i,j)+I(i,j+1)+I(i,j-1)+I(i+1,j)+I(i-1,j)$

对应的二阶微分卷积核为 ：
$\mathbf{m}=\left[\begin{array}{lll}0& 1& 0\\ 1& 4& 1\\ 0& 1& 0\end{array}\right]$

所以二阶微分检测边缘的方法就分两步：

1. 用上面的 Laplace 核与图像进行卷积；
2. 对卷积后的图像，取得那些卷积结果为0 的点。

Laplace 算子

拉普拉斯表达式

Laplace （拉普拉斯）算子是最简单的各向同性微分算子，一个二维图像函数的拉普拉斯变换是各向同性的二阶导数。下式为 Laplace 算子的表达式：
${\nabla }^{2}f(x,y)=\frac{{\partial }^{2}f(x,y)}{\partial x^2}+\frac{{\partial }^{2}f(x,y)}{\partial y^2}$
我们知道梯度的表达式为：$\nabla =\frac{\partial }{\partial x}\vec{i}+\frac{\partial }{\partial y}\vec{j}$
于是上式的推导过程就是：
${\nabla }^2\triangleq \nabla \cdot \nabla =\left(\frac{\partial }{\partial x}\vec{i}+\frac{\partial }{\partial y}\vec{j}\right)\cdot \left(\frac{\partial }{\partial x}\vec{i}+\frac{\partial }{\partial y}\vec{j}\right)=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$

图像中的Laplace 算子

考虑到图像是离散的二维矩阵，用差分近似微分可以得到：
$\frac{{\partial }^{2}f}{\partial x^2}=\frac{\partial G}{\partial x}=\frac{\partial [\mathrm{f}(\mathrm{i},\mathrm{j})-\mathrm{f}(\mathrm{i},\mathrm{j}-1)]}{\partial x}=\frac{\partial \mathrm{f}(\mathrm{i},\mathrm{j})}{\partial x}-\frac{\partial \mathrm{f}(\mathrm{i},\mathrm{j}-1)}{\partial x}$
$=[\mathrm{f}(\mathrm{i},\mathrm{j}+1)-\mathrm{f}(\mathrm{i},\mathrm{j})]-[\mathrm{f}(\mathrm{i},\mathrm{j})-\mathrm{f}(\mathrm{i},\mathrm{j}-1)]$
$=\mathrm{f}(\mathrm{i},\mathrm{j}+1)-2\mathrm{f}(\mathrm{i},\mathrm{j})+\mathrm{f}(\mathrm{i},\mathrm{j}-1)$
同理，可得：
$\frac{{\partial }_f^2}{\partial x^2}=\mathrm{f}(\mathrm{i}+1,\mathrm{j})-2\mathrm{f}(\mathrm{i},\mathrm{j})+\mathrm{f}(\mathrm{i}-1,\mathrm{j})$
于是有：
${\nabla }^2\mathrm{f}=\frac{{\partial }_f^2}{\partial x^2}+\frac{{\partial }_f^2}{\partial x^2}=\mathrm{f}(\mathrm{i}+1,\mathrm{j})+\mathrm{f}(\mathrm{i}-1,\mathrm{j})+\mathrm{f}(\mathrm{i},\mathrm{j}+1)+\mathrm{f}(\mathrm{i},\mathrm{j}-1)-4\mathrm{f}(\mathrm{i},\mathrm{j})$
用模板来表示为：
$\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$
还有一种常用的卷积模板为：
$\left[\begin{array}{ccc}-1& -1& -1\\ -1& 8& -1\\ -1& -1& -1\end{array}\right]$
有时我们为了在邻域中心位置取到更大的权值，还使用如下卷积模板：
$\left[\begin{array}{ccc}1& 4& 1\\ 4& -20& 4\\ 1& 4& 1\end{array}\right]$

Laplace算法过程

（1）遍历图像（除去边缘，防止越界），对每个像素做Laplancian模板卷积运算
（2）复制到目标图像，结束。

Laplace算子的旋转不变性证明

$\begin{array}{rl}{\nabla }^{2}f& =\frac{{\partial }^{2}f}{\partial x^{\prime 2}}+\frac{{\partial }^{2}f}{\partial y^{\prime 2}}\\ & =\frac{\partial }{\partial x^{\prime }}\left(\frac{\partial f}{\partial x^{\prime }}\right)+\frac{\partial }{\partial y^{\prime }}\left(\frac{\partial f}{\partial y^{\prime }}\right)\\ & =\frac{\partial }{\partial x^{\prime }}\left(\frac{\partial f}{\partial x}\frac{\partial x}{\partial x^{\prime }}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial x^{\prime }}\right)+\frac{\partial }{\partial y^{\prime }}\left(\frac{\partial f}{\partial x}\frac{\partial x}{\partial y^{\prime }}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial y^{\prime }}\right)\\ & =\frac{\partial }{\partial x^{\prime }}\left(\frac{\partial f}{\partial x}\cos \theta +\frac{\partial f}{\partial y}\sin \theta \right)+\frac{\partial }{\partial y^{\prime }}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right)\\ & =\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial x}\cos \theta +\frac{\partial f}{\partial y}\sin \theta \right)\frac{\partial x}{\partial x^{\prime }}+\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\cos \theta +\frac{\partial f}{\partial y}\sin \theta \right)\frac{\partial y}{\partial x^{\prime }}\\ & +\frac{\partial }{\partial x}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right)\frac{\partial x}{\partial y^{\prime }}+\frac{\partial }{\partial y}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right)\frac{\partial y}{\partial y^{\prime }}\\ & =\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial x}\cos \theta +\frac{\partial f}{\partial y}\sin \theta \right)\cos \theta +\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\cos \theta +\frac{\partial f}{\partial y}\sin \theta \right)\sin \theta \\ & +\frac{\partial }{\partial x}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \frac{\partial f}{\partial y}\right)(-\sin \theta )+\frac{\partial }{\partial y}\left(-\sin \theta \frac{\partial f}{\partial x}+\cos \theta \frac{\partial f}{\partial y}\right)\cos \theta \\ & =\frac{\partial }{\partial x}\frac{\partial f}{\partial x}+\frac{\partial }{\partial y}\frac{\partial f}{\partial y}\\ & =\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}\end{array}$

Laplace算子优缺点

Laplace算子具有旋转不变性，适用于仅注重边缘点所处的具体位置，而对边缘点附近的实际灰度差没有要求的情况。不过在边缘检测中并不常用拉普拉斯算子，而主要是用在判断像素是在边缘亮的一面还是暗的一面，主要有以下三点原因：
(1) 二阶导数算子与一阶导数算子相比，去除噪声的能力更弱；
(2) 该算子对边缘的方向检测不到；
(3) 该算子的幅值会产生双边元，抗噪能力弱。

LOG算子

1980年，Marr和Hildreth提出将Laplace算子与高斯低通滤波相结合，提出了LOG（Laplace and Guassian）算子，又称为马尔（Marr）算子。 该算子是先运用高斯滤波器平滑图像达到去除噪声的目的，然后用 Laplace 算子对图像边缘进行检测。这样既达到了降低噪声的效果，同时也使边缘平滑，并得到了延展。为了防止得到不必要的边缘，边缘点应该选取比某阈值高的一阶导数零交叉点。 LOG 算子已经成为目前对阶跃边缘用二阶导数过零点来检测的最好的算子。

LoG解决的问题

直接使用Laplace算法，去噪的能力是非常弱的，最终提取出的边缘信息极易被噪音干扰，如下图所示

由图可以看出，LoG解决的最重要的问题是在提取边缘信息之前给原始图像增添一层高斯滤波器，使得原始图像的梯度异常点大大减少，最终能够更有效地提取出边缘信息。

LoG算子的计算过程

在图像处理中，常用的二维高斯函数为 :
$G(x,y,\sigma )=\frac{1}{2\pi {\sigma }^2}{e}^{-\left(x^2+y^2\right)/2{\sigma }^2}$

拉普拉斯算子为 :
$\begin{array}{rl}{\nabla }^{2}f& =\frac{{\partial }^{2}f}{\partial x^{\prime 2}}+\frac{{\partial }^{2}f}{\partial y^{\prime 2}}\end{array}$

对二维高斯函数应用拉普拉斯算子得 :${\nabla }^{2}G=\frac{{\partial }^{2}G}{\partial x^2}+\frac{{\partial }^{2}G}{\partial y^2}=\frac{-2{\sigma }^2+x^2+y^2}{2\pi {\sigma }^6}{e}^{-\left(x^2+y^2\right)/2{\sigma }^2}$

LoG（Laplacian of Gaussian）算子定义为 :
$LoG={\sigma }^2{\nabla }^{2}G$

注意到LoG算子，该函数轴对称，且函数的平均值为0（在定义域内），所以用它与图像进行卷积计算并不会对完整的图像动态区域有所改变，而是会使图像变模糊（因为它相当平滑），且模糊程度与σ成正比。当σ较大时，高斯滤波起到了很好的平滑效果，较大程度地抑制了噪声，但同时使一些边缘细节丢失，降低了图像边缘的定位精度；当σ比较小时，有很强的图像边缘定位精度，反而信噪比较低。因此，在应用 LOG 算子时，如何选取适当的σ值很重要，要根据边缘的定位精度的需求以及噪声情况而定 。

LoG的卷积模板

LOG 算子的卷积模板通常采用 5×5的矩阵，如：

计算方法

其中左边这个模板是在高斯标准差为0.5时的逼近，右边的模板的高斯标准差为1。Normalize是一个正则函数，它确保模板系数的总和为1. 以便在均匀亮度区域不会检测到边缘。最后由于整数比浮点数更易于计算，模板的系数都会近似为整数。

LoG算法过程

（1）遍历图像（除去边缘，防止越界），对每个像素做Gauss -Laplancian模板卷积运算。
（2）复制到目标图像，结束。

DoG与LoG

由于数学上的关系, 我们可以简化 LOG 的计算一一这便是 DOG 算子。
DoG (Difference of Gaussian ) 算子定义为
$$DoG=G\left(x,y,{\sigma }_1\right)-G\left(x,y,{\sigma }_2\right)$$
下面我们来证明为何 DoG 能近似替代 LoG。
对二维高斯函数关于 $\sigma$ 求一阶偏导数得
$$\frac{\partial G}{\partial \sigma }=\frac{-2{\sigma }^2+x^2+y^2}{2\pi {\sigma }^5}{e}^{-\left(x^2+y^2\right)/2{\sigma }^2}$$
不难发现
$$\frac{\partial G}{\partial \sigma }=\sigma {\nabla }^{2}G$$
在 $DoG$ 算子中, 令 $\sigma 1=k\sigma 2=k\sigma$, 则
$$DoG=G(x,y,k\sigma )-G(x,y,\sigma )$$
进一步地
$$\frac{\partial G}{\partial \sigma }=\underset{\Delta \sigma \to 0}{\lim }\frac{G(x,y,\sigma +\Delta \sigma )-G(x,y,\sigma )}{(\sigma +\Delta \sigma )-\sigma }\approx \frac{G(x,y,k\sigma )-G(x,y,\sigma )}{k\sigma -\sigma }$$
因此
$$\sigma {\nabla }^{2}G=\frac{\partial G}{\partial \sigma }\approx \frac{G(x,y,k\sigma )-G(x,y,\sigma )}{k\sigma -\sigma }$$
[日]
$$G(x,y,k\sigma )-G(x,y,\sigma )\approx (k-1){\sigma }^2{\nabla }^{2}G$$
这表明 DoG 算子可以近似于 LoG 算子, 证毕。
于是, 使用 DoG 算子, 让我们只需对图像进行两次高斯平滑再将结果相减就可以近似 得到 LOG 作用于图像的效果了。
值得注意的是, 当我们用 DOG 算子代替 LOG 算子与图像卷积的时候:
$$DoG\left(x,y,{\sigma }_1,{\sigma }_2\right)\ast I(x,y)=G\left(x,y,{\sigma }_1\right)\ast I(x,y)-G\left(x,y,{\sigma }_2\right)\ast I(x,y)$$
近似的 LOG 算子值的选取:
$${\sigma }^2=\frac{{\sigma }_1^2{\sigma }_2^2}{{\sigma }_1^2-{\sigma }_2^2}\ln \left[\frac{{\sigma }_1^2}{{\sigma }_2^2}\right]$$
当使用这个值时, 可以保证 LoG 和 DoG 的过零点相同, 只是幅度大小不同。

LoG算子优缺点

值得肯定的是，LoG这种方法寻找二阶导数是很稳定的。高斯平滑有效地抑制了距离当前像素3σ范围内的所有像素的影响，这样Laplace算子就构成了一种反映图像变化的有效而稳定的度量。 但是，这种传统的二阶导数过零点技术也有缺点。第一，对形状作了过分的平滑。第二，它有产生环形边缘的倾向。

Canny算子

Canny算子概述

Canny边缘检测算法是1986年有John F. Canny开发出来一种基于图像梯度计算的边缘检测算法，同时Canny本人对计算图像边缘提取学科的发展也是做出了很多的贡献。尽管至今已经许多年过去，但是该算法仍然是图像边缘检测方法经典算法之一。
Canny 根据以前的边缘检测算子以及应用，归纳了如下三条准则：

(1) 信噪比准则：避免真实的边缘丢失，避免把非边缘点错判为边缘点；
(2) 定位精度准则：得到的边缘要尽量与真实边缘接近；
(3) 单一边缘响应准则：单一边缘需要具有独一无二的响应，要避免出现多个响应，并最大抑制虚假响应。
以上三条准则是由 Canny 首次明确提出并对这个问题进行完全解决的，虽然在他之前有人提出过类似的要求。更为重要的是， Canny 同时给出了它们的数学表达式（现以一维为例），这就转化成为一个泛函优化的问题。

Canny算子检测步骤

经典的Canny边缘检测算法通常都是从高斯模糊开始，到基于双阈值实现边缘连接结束。但是在实际工程应用中，考虑到输入图像都是彩色图像，最终边缘连接之后的图像要二值化输出显示，所以完整的Canny边缘检测算法实现步骤如下：

1. 彩色图像转换为灰度图像
2. 对图像进行高斯模糊
3. 计算图像梯度，根据梯度计算图像边缘幅值与角度
4. 非极大值抑制（边缘细化）
5. 双阈值检测
6. 通过抑制孤立的弱边缘完成边缘检测
7. 二值化图像输出结果

Canny算子各步骤详解

彩色图像转换为灰度图像

根据彩色图像RGB转灰度公式：gray = R * 0.299 + G * 0.587 + B * 0.114。

对图像进行高斯模糊

为了尽可能减少噪声对边缘检测结果的影响，所以必须滤除噪声以防止由噪声引起的错误检测。为了平滑图像，使用高斯滤波器与图像进行卷积，该步骤将平滑图像，以减少边缘检测器上明显的噪声影响。大小为(2k+1)x(2k+1)的高斯滤波器核的生成方程式由下式给出：
$H_{ij}=\frac{1}{2\pi {\sigma }^2}\exp \left(-\frac{(i-(k+1){)}^2+(j-(k+1){)}^2}{2{\sigma }^2}\right);1\le i,j\le (2k+1)$
下面是一个sigma = 1.4，尺寸为3x3的高斯卷积核的例子（需要注意归一化）：
$H=\left[\begin{array}{lll}0.0924& 0.1192& 0.0924\\ 0.1192& 0.1538& 0.1192\\ 0.0924& 0.1192& 0.0924\end{array}\right]$
若图像中一个3x3的窗口为A，要滤波的像素点为e，则经过高斯滤波之后，像素点e的亮度值为：
$e=H\ast A=\left[\begin{array}{lll}{\mathrm{h}}_{11}& {\mathrm{h}}_{12}& {\mathrm{h}}_{13}\\ {\mathrm{h}}_{21}& {\mathrm{h}}_{22}& {\mathrm{h}}_{23}\\ {\mathrm{h}}_{31}& {\mathrm{h}}_{32}& {\mathrm{h}}_{33}\end{array}\right]\ast \left[\begin{array}{lll}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]=\mathrm{sum}\left(\left[\begin{array}{lll}\mathrm{a}\times {\mathrm{h}}_{11}& \mathrm{b}\times {\mathrm{h}}_{12}& \mathrm{c}\times {\mathrm{h}}_{13}\\ \mathrm{d}\times {\mathrm{h}}_{21}& \mathrm{e}\times {\mathrm{h}}_{22}& \mathrm{f}\times {\mathrm{h}}_{23}\\ \mathrm{g}\times {\mathrm{h}}_{31}& \mathrm{h}\times {\mathrm{h}}_{32}& \mathrm{i}\times {\mathrm{h}}_{33}\end{array}\right]\right)$
其中*为卷积符号，sum表示矩阵中所有元素相加求和。 重要的是需要理解，高斯卷积核大小的选择将影响Canny检测器的性能。尺寸越大，检测器对噪声的敏感度越低，但是边缘检测的定位误差也将略有增加。一般5x5是一个比较不错的trade off。

计算图像梯度，根据梯度计算图像边缘幅值与角度

图像中的边缘可以指向各个方向，因此Canny算法使用四个算子来检测图像中的水平、垂直和对角边缘。边缘检测的算子（如Roberts，Prewitt，Sobel等）返回水平Gx和垂直Gy方向的一阶导数值，由此便可以确定像素点的梯度G和方向theta 。
$G=\sqrt{G_x^2+G_y^2}$
$\theta =\arctan \left(G_y/G_x\right)$
其中G为梯度强度， theta表示梯度方向，arctan为反正切函数。

非极大值抑制（边缘细化）

非极大值抑制是一种边缘稀疏技术，非极大值抑制的作用在于“瘦”边。对图像进行梯度计算后，仅仅基于梯度值提取的边缘仍然很模糊。对于标准3，对边缘有且应当只有一个准确的响应。而非极大值抑制则可以帮助将局部最大值之外的所有梯度值抑制为0，对梯度图像中每个像素进行非极大值抑制的算法是： 1) 将当前像素的梯度强度与沿正负梯度方向上的两个像素进行比较。 2) 如果当前像素的梯度强度与另外两个像素相比最大，则该像素点保留为边缘点，否则该像素点将被抑制。 通常为了更加精确的计算，在跨越梯度方向的两个相邻像素之间使用线性插值来得到要比较的像素梯度，现举例如下：

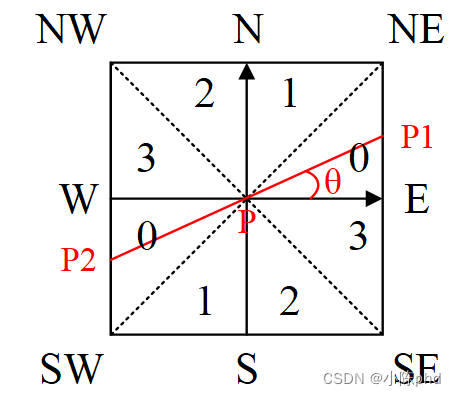
如上图所示，将梯度分为8个方向，分别为E、NE、N、NW、W、SW、S、SE，其中0代表0°_{45°,1代表45°}90°，2代表-90°_{-45°，3代表-45°}0°。像素点P的梯度方向为theta，则像素点P1和P2的梯度线性插值为：
$\tan (\theta )=G_y/G_x$
$G_{p1}=(1-\tan (\theta ))\times E+\tan (\theta )\times NE$
$G_{p2}=(1-\tan (\theta ))\times W+\tan (\theta )\times SW$
因此非极大值抑制的伪代码描写如下：

if $G_p\ge G_{p1}$ and $G_p\ge G_{p2}$
$G_p$ may be an edge
else
$G_p$ should be sup pressed
需要注意的是，如何标志方向并不重要，重要的是梯度方向的计算要和梯度算子的选取保持一致。

双阈值检测

在施加非极大值抑制之后，剩余的像素可以更准确地表示图像中的实际边缘。然而，仍然存在由于噪声和颜色变化引起的一些边缘像素。为了解决这些杂散响应，必须用弱梯度值过滤边缘像素，并保留具有高梯度值的边缘像素，可以通过选择高低阈值来实现。如果边缘像素的梯度值高于高阈值，则将其标记为强边缘像素；如果边缘像素的梯度值小于高阈值并且大于低阈值，则将其标记为弱边缘像素；如果边缘像素的梯度值小于低阈值，则会被抑制。阈值的选择取决于给定输入图像的内容。
双阈值检测的伪代码描写如下：

if $G_p\ge$ HighThreshold
$G_p$ is an strong edge
else if $G_p\ge$ Low Threshold
$G_p$ is an weak edge
else
$G_p$ should be sup pressed

通过抑制孤立的弱边缘完成边缘检测

到目前为止，被划分为强边缘的像素点已经被确定为边缘，因为它们是从图像中的真实边缘中提取出来的。然而，对于弱边缘像素，将会有一些争论，因为这些像素可以从真实边缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果，应该抑制由后者引起的弱边缘。通常，由真实边缘引起的弱边缘像素将连接到强边缘像素，而噪声响应未连接。为了跟踪边缘连接，通过查看弱边缘像素及其8个邻域像素，只要其中一个为强边缘像素，则该弱边缘点就可以保留为真实的边缘。 抑制孤立边缘点的伪代码描述如下：

if $G_p==$ LowThreshold and $G_p$ connected to a strong edge pixel $G_p$ is an strong edge
else
$G_p$ should be sup pressed

二值化图像输出结果

将结果二值化输出，即将图像上的像素点的灰度值设置为0或255，也就是将整个图像呈现出明显的黑白效果的过程。

Canny算子优缺点

Canny 算子在二维空间的检测效果、定位性能及抗噪性能方面都更要优于 LOG 算子。
Canny 算子的不足之处是对于无噪声的图像会使图像边缘变模糊。(高斯滤波属于低通滤波，去除一些高频细节)
为使检测效果更好，我们在运用该算子时一般选取稍大的滤波尺度，但是这样做易使图像的某些边缘细节特征丢失掉。

链接: Glab.