1、拉普拉斯算子 ∇ 2 \nabla^ 2 ∇2
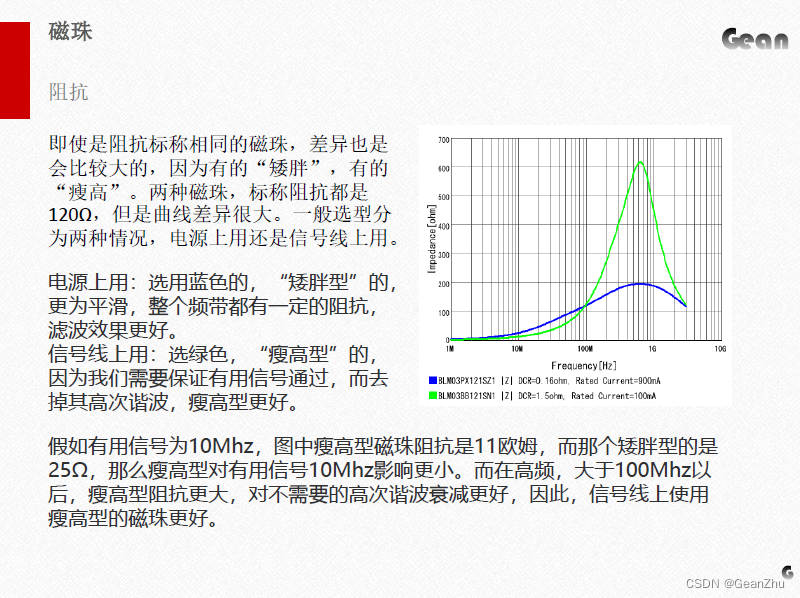
拉普拉斯算子有很多用途,在物理中常用于波动方程、热传导方程和亥姆霍兹方程的数学模型;在静电学中,拉普拉斯方程和泊松方程的应用随处可见;在数学中,经拉普拉斯算子运算运算为零的函数称为调和函数。可表示为: ∇ ⋅ ( ∇ u ) = ∇ 2 u \nabla \cdot (\nabla u)=\nabla^2 u ∇⋅(∇u)=∇2u
拉普拉斯算子在不同的坐标系下具有不同的表达形式:
- 直角坐标系 ∇ 2 u = ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 \nabla^2 u=\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2} ∇2u=∂x2∂2u+∂y2∂2u+∂z2∂2u
- 圆柱坐标系 ∇ 2 u = 1 ρ ∂ ∂ ρ ( ρ ∂ u ∂ ρ ) + 1 ρ 2 ∂ 2 u ∂ ϕ 2 + ∂ 2 u ∂ z 2 \nabla^{2} u=\frac{1}{\rho} \frac{\partial}{\partial \rho}\left(\rho \frac{\partial u}{\partial \rho}\right)+\frac{1}{\rho^{2}} \frac{\partial^{2} u}{\partial \phi^{2}}+\frac{\partial^{2} u}{\partial z^{2}} ∇2u=ρ1∂ρ∂(ρ∂ρ∂u)+ρ21∂ϕ2∂2u+∂z2∂2u
- 球坐标系 ∇ 2 u = 1 r 2 ∂ ∂ r ( r 2 ∂ u ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ u ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 u ∂ ϕ 2 \nabla^{2} u=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial u}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial u}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2} u}{\partial \phi^{2}} ∇2u=r21∂r∂(r2∂r∂u)+r2sinθ1∂θ∂(sinθ∂θ∂u)+r2sin2θ1∂ϕ2∂2u
- 广义正交曲线坐标系 ∇ 2 ϕ = 1 h 1 h 2 h 3 [ ∂ ∂ u 1 ( h 2 h 3 h 1 ∂ ϕ ∂ u 1 ) + ∂ ∂ u 2 ( h 1 h 3 h 2 ∂ ϕ ∂ u 2 ) + ∂ ∂ u 3 ( h 1 h 2 h 3 ∂ ϕ ∂ u 3 ) ] \nabla^{2} \phi=\frac{1}{h_{1} h_{2} h_{3}}\left[\frac{\partial}{\partial u_{1}}\left(\frac{h_{2} h_{3}}{h_{1}} \frac{\partial \phi}{\partial u_{1}}\right)+\frac{\partial}{\partial u_{2}}\left(\frac{h_{1} h_{3}}{h_{2}} \frac{\partial \phi}{\partial u_{2}}\right)+\frac{\partial}{\partial u_{3}}\left(\frac{h_{1} h_{2}}{h_{3}} \frac{\partial \phi}{\partial u_{3}}\right)\right] ∇2ϕ=h1h2h31[∂u1∂(h1h2h3∂u1∂ϕ)+∂u2∂(h2h1h3∂u2∂ϕ)+∂u3∂(h3h1h2∂u3∂ϕ)]
下面的代码利用公式 ∇ 2 F ⃗ = ∇ ( ∇ ⋅ F ⃗ ) − ∇ × ( ∇ × F ⃗ ) \nabla^{2} \vec{F}=\nabla(\nabla \cdot \vec{F})-\nabla \times(\nabla \times \vec{F}) ∇2F=∇(∇⋅F)−∇×(∇×F)对矢量函数 V V V进行矢量的拉普拉斯运算,并显示最终的结果。
syms x y z
V = [x^2*y, y^2*z, z^2*x];
vars = [x y z];
gradient(divergence(V,vars)) - curl(curl(V,vars),vars)
运行结果:

2、del2函数
del2是离散拉普拉斯算子,利用差分运算得到微分运算的近似值。基本格式如下:
-
L = d e l 2 ( u ) L=del2(u) L=del2(u)
该函数返回标量函数 u u u的拉普拉斯微分运算的离散逼近,所有点之间离散化间距取默认值1。 -
L = d e l 2 ( u , h ) L=del2(u,h) L=del2(u,h)该函数返回标量函数 u u u的拉普拉斯微分运算的近似值。所有维度上的点指定了一个均匀的标量间距 h h h。
-
L = d e l 2 ( u , h x , h y , … , h N ) L=del2(u,hx,hy,…,hN) L=del2(u,hx,hy,…,hN)
与前面类似的,指定 h x , h y , … , h N hx,hy,…,hN hx,hy,…,hN为 u u u的每个维度上的点的间距。需要注意的是,根据有限差分的理论,del2得到的是拉普拉斯运算的1/4的近似值,而不是运算本身。
3、拉普拉斯矩阵的可视化
下面的代码计算一个余弦函数的一维拉普拉斯矩阵。
x = linspace(-2*pi,2*pi); %定义x向量
U = cos(x); %计算cos(x)
L = 4*del2(U,x); %计算U的拉普拉斯,注意系数4
plot(x,U,x,L) %画出U和U的拉普拉斯曲线
legend('U(x)','L(x)','Location','Best') %给出图例
结果如下:

对于多元函数,也可以计算其对应的拉普拉斯运算的结果,下面的代码是计算并绘制二维函数的离散拉普拉斯运算结果。
[x,y] = meshgrid(-5:0.25:5,-5:0.25:5); %定义函数在x,y方向的区域
U = 1/3.*(x.^4+y.^4); %定义函数U
h = 0.25; %U中各点的间距在所有方向上都相等,所以可以指定一个间距h
L = 4*del2(U,h); %计算U的拉普拉斯变换
surf(x,y,L);
grid on;
title('Plot of $\Delta U(x,y) = 4x^2+4y^2$','Interpreter','latex')
xlabel('x');
ylabel('y');
zlabel('z');
view(35,14);
结果如下: